沥青混合料黏塑性变形的不同形式描述

叶 永，陈洪凯

(1.重庆交通大学 土木建筑学院，重庆 400074；2.三峡大学 水利与环境学院，湖北 宜昌 443002)

沥青混合料是由沥青、骨料和空隙组成的三相复合体，组成材料性质各异，力学本构模型描述相当复杂[1]。一般通过总变形分解，构建蠕变本构模型。彭妙娟，等[2-3]在广义的Maxwell模型基础上串联一个弹塑性模型，提出了沥青混合料非线性黏弹-弹塑性模型，Y.Lu，B.Huang，等[4-5]通过把沥青混合料总变形分解成弹性、黏弹性和黏塑性变形，再采用不同方式描述这些变形，也提出了不同形式的黏弹塑性本构模型。上述这些模型涉及参数较多、不适用单轴实验结果。基于此，笔者在大量实验的基础上，提出了反映沥青混合料单轴蠕变特性的黏弹塑蠕变本构模型，进行了不同模型效果研究工作[6-9]，通过与实验结果的对比，验证了提出模型的合理性和有效性，也得出了一些有益结论。研究过程中可以得知沥青混合料呈现明显的黏塑性流变特点[10]，对其黏塑性变形研究具有更重要实际意义。笔者结合前期工作，进一步明确对黏塑性不同描述的差异，解析沥青混合料的黏塑特性，优化其力学本构关系，为沥青混合料的力学性能研究打下稳固基础。

1 黏弹塑蠕变本构模型

1.1 蠕变变形特征

图1显示了沥青混合料在一个循环载荷(加载后卸载)下的蠕变变形曲线。曲线分为3个阶段：在加载的初始阶段，应变迅速增加，主要产生可恢复弹性变形εe和不可恢复塑性变形εp；载荷继续增加，变形进入第2阶段，应变随时间逐步上升，应变率逐渐减小并趋于稳定，主要产生黏弹性变形εve和黏塑性变形εvp；此时卸载，变形进入弹性恢复阶段，这一过程主要发生弹性变形，随着载荷逐渐卸掉，发生的变形部分逐渐恢复，部分不能恢复。能够随时间完全恢复的为黏弹性变形，而不能恢复的为黏塑性变形，其中还存在一部分最初发生的塑性变形。

图1 沥青混合料变形分解Fig.1 Deformation and decomposition of asphalt mixtures

图1显示了沥青混合料在一个加载-卸载循环载荷下的蠕变变形曲线。曲线分为4个阶段：第1阶段，在加载的初始阶段，应变迅速增加，主要产生可恢复弹性变形εe和不可恢复塑性变形εp。载荷继续增加，变形进入第2阶段，应变随时间逐步上升，应变率逐渐减小并趋于稳定，主要产生黏弹性变形εve和黏塑性变形εvp。此时卸载，变形进入第3阶段，即弹性恢复阶段，这一过程主要发生弹性变形。随着载荷逐渐卸掉，进入第4阶段，发生的变形部分逐渐恢复，部分不能恢复，能够随时间完全恢复的为黏弹性变形，而不能恢复的为黏塑性变形，其中还存在一部分最初发生的塑性变形。

如果把弹性变形和塑性变形作为弹塑性变形一起考虑，则沥青混合料的总变形可以分解为：

ε=εep+εve+εvp

(1)

式中：εep为沥青混合料弹塑性变形；εve为黏弹性变形；εvp为黏塑性变形。

图2是沥青混合料试样在40℃，0.2 MPa应力作用下的蠕变曲线。其蠕变过程可分为3个阶段，第1阶段为初始蠕变(0 s750 s)，变形快速加大，应变率随之增加，试样达到破坏状态，实验停止。

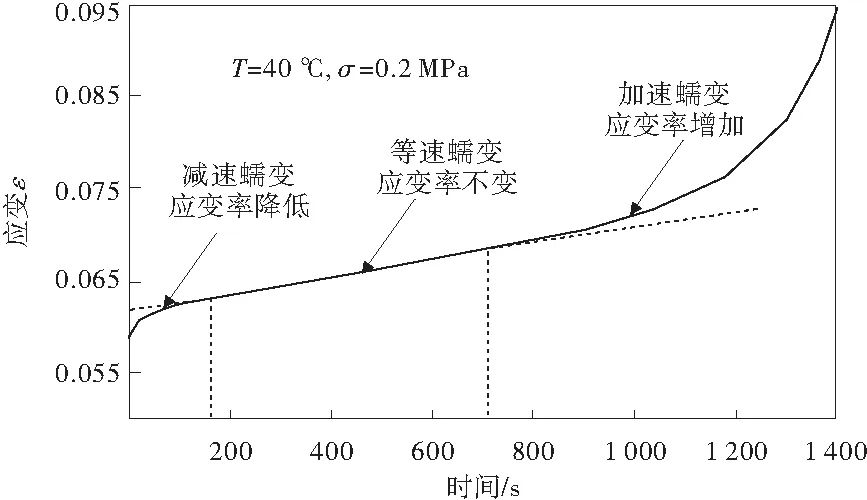
图2 试样在40℃时的蠕变实验曲线Fig.2 Curve stress creep test of specimen at 40℃

1.2 模型构架

如果将弹塑性、黏弹性和黏塑性变形组合起来，按照式(1)应变关系串联在一起，即可得到沥青混合料黏弹塑蠕变本构模型，如图3。图中3个串联应力分别为弹塑性应力、黏弹性应力和黏塑性应力，即σep,σve,σvp，应变为εep,εve,εvp。在一维应力下，满足：

σ=σep=σve=σvp

(2)

ε=εep+εve+εvp

(3)

图3 黏弹塑性本构模型Fig.3 Constitutive scheme for the visco-elast-plastic model

图3左框描述弹塑性变形，由弹簧E2元件和圣维南滑块并联后，再与弹簧E1元件串联组成，令σs1为滑块初始屈服极限，本构方程为：

(4)

图3中间框为黏弹性变形，由弹簧E3元件和黏壶η1并联组成，本构方程为：

(5)

图3右框为黏塑性变形，由圣维南滑块和黏壶η2并联组成，σs2为滑块初始屈服极限，本构方程形式根据对黏塑性变形不同假设而有不同描述，分别对应3个本构模型(模型1～模型3)。

2 黏塑性描述

2.1 基于黏滞阻力器描述

笔者提出非线性黏滞阻尼器来描述黏塑性变形，认为该阻尼器所受应力与其蠕变加速度成正比，对于一维应力，应变εvp与应力σvp关系为：

(6)

由变形的初始条件得到应变ε2与时间t关系为：

(7)

在常应力σ=σ0的作用下，模型1的蠕变方程为：

(8)

2.2 基于黏性系数描述

改变黏塑性系数η2来描述黏塑性变形。对于一维应力，应变εvp与应力σvp关系为：

(9)

再假定黏塑性系数η2与时间t的关系为：

(10)

式中：A,B为常数；η0为初始黏性系数，可通过实验确定。

由变形的初始条件得到应变εvp与时间t关系为：

(11)

在常应力σ=σ0的作用下，模型2的蠕变方程为：

(12)

2.3 基于应变硬化理论描述

利用应变硬化模型描述黏塑性变形，对于一维应力，提出应力函数g(σ)与应变εvp关系为：

(13)

(14)

式中：C=A/B。

在模型中引用<σvp-σs2>，则式(14)写成：

(15)

式中：C，m，n为材料常数，由实验结果确定。

在常应力σ=σ0的作用下，模型3蠕变方程为：

(16)

3 不同形式描述比较

3.1 模型参数确定

编制非线性最小二乘法程序，在程序中输入合适的模型参数初始值，通过非线性循环反演即可求得模型各个参数。模型参数的取值影响着模型拟合结果，因此，在循环反演中要多次试算。

模型中涉及从黏弹性到黏塑性过渡，引入了极限应力概念。在此应力下，变形为黏弹性，超过此应力，材料进入黏塑性变形。因此首先要确定沥青混合料极限应力σs。经过多次分析及实验结果，取试样长时间处于等速蠕变对应的加载应力0.05 MPa为应力极限值具有合理性。表1列出了在40℃下施加不同应力时3个模型参数的拟合结果。相关系数表明了拟合程序具有较好的精度。

表1 模型1～模型3不同应力作用下的参数值

3.2 模型对比

图4给出了在较低应力水平下(0.10，0.15 MPa)，3种模型预测值与实验值的对比结果。由图可知，3种不同形式模型与实验结果吻合很好，反映了3种不同形式模型能够拟合较低应力作用下沥青混合料整个蠕变过程，且具有较好精度。

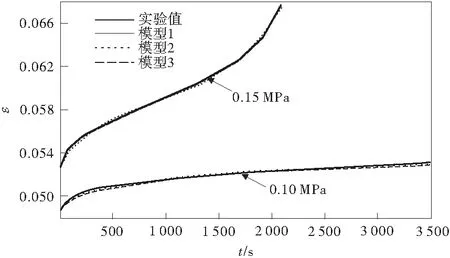
图4 40℃下低应力模型预测比较Fig.4 Comparison of three models at lower stresses at 40℃

图5给出了在较高应力水平下(0.20，0.25，0.30 MPa)，3种模型预测值与实验值的对比结果。由图5可知，3种不同形式模型反映了沥青混合料蠕变的基本特性，但模型3在描述第1蠕变过程存在一定误差，而模型1和模型2的预测较接近沥青混合料整个蠕变实验曲线。结合表1中平均相关系数，可以认为，在研究沥青混合料黏塑性应变时，采取模型2的假设更为有效，且得到的黏弹塑本构模型更能反映沥青混合料在不同载荷条件下整个蠕变过程，其次为模型1的假设。看来黏性材料的黏性系数是一个重要参数，对材料黏性特性描述具有较大影响，体现了材料的时间率相关性。

图5 40℃下高应力模型预测比较Fig.5 Comparison of three models at higher stresses at 40℃

4 结 论

1)实验结果表明，载荷作用下沥青混合料变形可以分解为弹塑性、黏弹性和黏塑性3个变形分量。采用由3个变形分量组成的黏弹塑本构模型，符合沥青混合料时间效应的变形特点。该本构模型的描述方法对黏弹性材料具有合理性。

2)采用3种不同形式描述黏塑性得到的力学模型，其预测值与实验结果进行对比，较低应力水平下，都能较好吻合实验结果，在较高应力水平下，模型2的预测结果更接近沥青混合料实验蠕变曲线，模型1次之，模型3预测初始蠕变效果较差。可见，模型1、模型2的假定侧重于时间效应，更符合黏弹性材料的力学描述，体现时间的率相关性，模型3采用的应变硬化假定侧重于应变过程描述，在黏弹性材料的应用上具有一定误差。

3)由于实验条件限制，笔者仅描述了材料的单轴压缩与蠕变实验，由此得到的沥青混合料黏弹塑变形特性具有局限性。为揭示沥青混合料变形的一般规律，更好地与实际相结合，需要进行多轴实验研究。

[1] 孙立军.沥青路面结构行为理论[M].北京:人民交通出版社,2005.

Sun Lijun.Structural Behavior Study for Asphalt Pavements [M].Beijing: China Communications Press, 2005.

[2] 彭妙娟,许志鸿.沥青路面永久变形的非线性本构模型研究[J].中国科学G辑,2006,36(4):415-426.

Peng Miaozhuan,Xuzhihong.Non-liner constitutive model of permanent deformation for asphalt pavement [J].Science in China:Series G, 2006, 36(4): 415-426.

[3] 彭妙娟,许志鸿.沥青路面永久变形的非线性黏弹-弹塑性本构模型[J].交通运输工程学报,2007,7(5):41-47.

Peng Miaozhuan,Xuzhihong.Nonliner viscoelastic-elastoplastic constitutive model of permanent deformation for asphalt pavement [J].Journal of Traffic and Transportation Engineering, 2007, 7(5): 41-47.

[4] Lu Y,Wright P J.Numerical approach of visco-elastoplastic analysis for asphalt mixtures [J].Computers and Structures,1998,69:139-147.

[5] Huang B,Mohammad L.Development of a thermo-viscoplastic constitutive model for HMA mixtures [J].Journal of the Association of Asphalt Paving Technologists, 2002, 71:594-618.

[6] Ye Yong,Yang Xinhua,Chen Chuanyao.Experimental researches on visco-elastoplastic constitutive model of asphalt mastic [J].Construction and Building Materials, 2009, 23(10): 3161-3165.

[7] Ye Yong,Yang Xinhua,Chen Chuanyao.Viscoelastoplastic constitutive model for creep deformation behavior of asphalt sand [J].Journal of Central South University of Technology, 2008,15(S 1):13-16.

[8] Ye Yong,Yang Xinhua,Chen Chuanyao.The viscoplastic behavior of asphalt mixture in compression [C]// Engineering Pacificity and Its Applications:Proceeding of The 10th Asia-Pacific Conference,Wuhan,China,November15-17,2010.Singapore:World Scientific Publishing Co.Pte.Ltd., 2011.

[9] 叶永,杨新华,陈传尧.沥青砂蠕变特性及力学模型研究[J].公路,2009(2):121-124.

Ye Yong,Yang Xinhua,Chen Chuanyao.Research on creep behavior and mechanical model of asphalt sand [J].Highway,2009(2):121-124.

[10] Bandyopadhyaya R,Das A,Basu S.Numerical simulation of mechanical behavior of asphalt mix [J].Construction and Building Materials, 2008, 22(6): 1051-1058.