被动式半捷联平台的动力学模型及其稳定性分析

段晓敏，李杰，刘俊

(中北大学仪器科学与动态测试教育部重点实验室，山西 太原030051)

0 引言

被动式半捷联平台的研究是为了解决捷联式惯性导航系统在某些高速滚转飞行的制导炮弹中无法有效应用的问题。弹体的高速滚转会使得微机电系统(MEMS)陀螺仪无法有效测量滚转角速率，从而不能准确地建立姿态矩阵［1-2］。被动式半捷联平台是一种采用机械装置实现与弹体滚转隔离的惯性平台，被动式半捷联平台可以使微惯性测量单元(MIMU)在滚转方向保持稳定，而在俯仰和偏航方向保持捷联。影响被动式半捷联平台性能的因素有很多，其中弹体的飞行俯仰角是一个非常重要的影响因素，研究弹体飞行俯仰角的变化与被动式半捷联平台的稳定性关系具有重要的工程意义。

目前应用于小口径常规火箭弹的滚转稳定方案通常是采用伺服电机在滚转轴稳定惯导系统，这种方案由于伺服电机的引入从而导致其抗过载能力较差。Imbault 等介绍了美国桑迪亚国家实验室研发的一种微小型滚转稳定式惯性测量系统，可应用于低过载、高转速火箭弹的姿态测量［3］。王晨等对一种火箭弹大动态单轴平台惯导系统的姿态算法进行了研究［4］。

无陀螺捷联惯导系统可以应用于高速滚转制导炮弹的姿态测量，但测量精度较低。在无陀螺捷联惯导系统中引入磁传感器对于测量弹体姿态有一定帮助，但磁传感器通常容易受到外界干扰而产生较大的误差。美国的ANSR 炮弹使用的是由6 个加速度计和一个三轴磁传感器组成的捷联式惯性导航系统，Ohlmeyer 等对此系统做了介绍［5］。由MEMS 传感器组成的低成本MIMU 和磁传感器的组合系统被用于滚转炮弹姿态的测试，Davis 对此作了研究［6］。刘朝华等研究了利用MEMS 加速度计测量弹体滚转角的方法［7］。李枚等针对振动和高速自旋的环境对微惯性测量单元与地磁传感器组合导航方法进行了研究［8］。

本文给出的被动式半捷联平台，采用了由质量偏心结构提供回复力矩的设计实现平台在弹体滚转轴的稳定。该平台可以给MIMU 提供合适的应用环境。这种方案避免了伺服电机的使用，同时MIMU由适用于高过载环境下的MEMS 工艺制造的三正交陀螺仪和三正交加速度计组成，从而可以提高系统整体的抗过载能力，同时这种平台可以满足制导炮弹对惯性测量系统的小体积和低成本的要求。

本文对被动式半捷联平台进行了动力学建模，得到了平台内筒的运动微分方程。通过软件仿真计算和高速转台实验研究了弹体飞行俯仰角对平台稳定性的影响。主要内容包括:被动式半捷联平台组成及工作原理，动力学建模，方程的数值求解和地面半实物仿真实验。

1 平台组成及工作原理

本文给出的被动式半捷联平台的设计利用了复摆在重力作用下的运动原理。其核心是采用了质量块偏心安装的结构获得回复力矩来平衡由弹体的滚转运动对平台引起的摩擦力矩从而让平台获得稳定。如图1所示为复摆运动原理图，当复摆受外力矩作用离开竖直方向的平衡位置后，由于复摆受到重力作用的原因，会产生回到平衡位置的回复力矩，从而维持复摆稳定在平衡位置附近。图2为被动式半捷联平台的结构剖面图，平台主要由发射过载转移装置、轴承、质量块、MIMU、电池和解算电路板组成。两个深沟球轴承支撑起一个内筒，内筒内部用来安装MIMU、解算电路板、电池和质量块。质量块用来降低内筒相对弹轴的质心位置。发射过载转移装置用来承受在发射瞬间内筒向后的冲击力。弹体在飞行过程中高速滚转时，平台内筒利用质量偏心产生的回复力矩通过轴承与弹体滚转轴保持隔离。

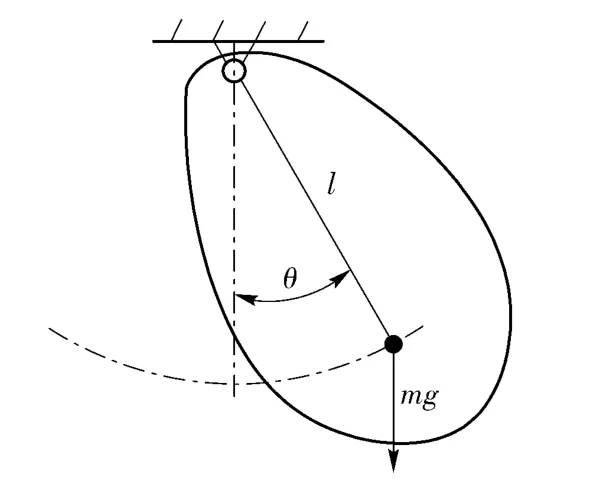
图1 复摆运动原理示意图Fig.1 Schematic diagram of compound pendulum motion

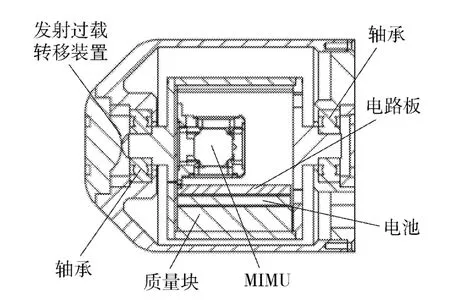
图2 平台结构剖面图Fig.2 Sectional drawing of platform

被动式半捷联惯性测量系统的工作原理如图3所示，弹体飞行的俯仰角为α(t)，弹体高速滚转，半捷联平台安装在弹体内部，平台内部安装有MIMU和解算模块，平台和弹体之间相对转速信息通过光电编码器测出并由无线传输装置传送至平台内部的解算模块。

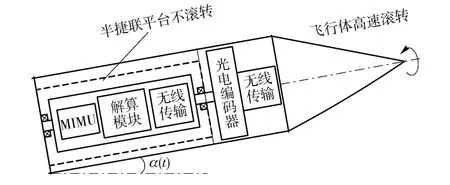
图3 被动式半捷联惯性测量系统工作示意图Fig.3 Schematic diagram of the partial strapdown inertial measurement system

2 平台的动力学模型建立

首先分析弹体在飞行过程中的受力情况，假设弹体飞行时的攻角很小，弹体的受力情况如图4所示，弹体在空中主要受到竖直向下的重力、垂直于弹轴方向的升力、分别沿弹轴前后两个方向的推力和阻力的作用。另外，弹体在竖直方向的加速度为av(t)，其大小由重力和升力在竖直方向的分力的合力决定。

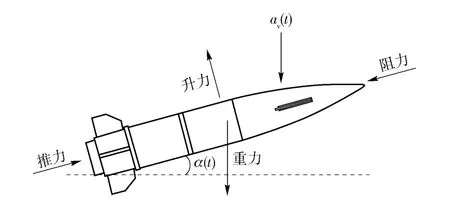
图4 炮弹飞行时受力示意图Fig.4 Force condition of the flying projectile

根据弹体在飞行时的受力情况和运动状态可以分析得出安装在其内部的被动式半捷联平台内筒的受力情况。如图5所示，在弹体飞行过程中，由于炮弹的旋转运动，使得弹体与半捷联平台内筒之间会通过轴承滚动产生摩擦力的作用。在竖直方向上，半捷联式平台内筒受到重力作用。在径向上，由于炮弹受到空气升力的作用，半捷联平台内筒会受到轴承对其支撑力的作用。在轴向上，由于炮弹受到推力和空气阻力的作用，半捷联平台内筒也会受到轴承对其支撑力的作用。这里两个支撑力分别构成了轴承的轴向载荷与径向载荷。图5中，C 为内筒质心，l 为摆的等效摆长。

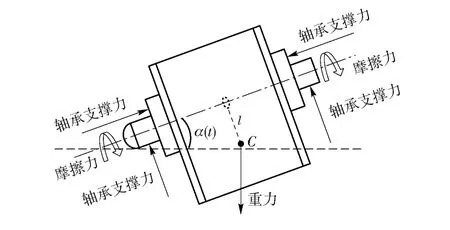
图5 平台内筒受力示意图Fig.5 Force condition of the platform’s inner cylinder

根据图4弹体和图5平台内筒的受力情况，结合需要解决的问题，建立了如图6所示的简化力学模型。图6(a)中，一个转动惯量为I0、质量为m、摆长为l 的摆，在摩擦力矩Mf和重力G 的作用下产生的摆动角度为θ(t). 摆的支撑体(实际为弹体)在竖直方向上受到重力Gp的作用，同时还受到支撑力Fs(实际为升力)的作用，摆的支撑体在Gp和Fs的作用下在竖直方向形成加速度av(t). 另外，图6(a)中的摆与弹体俯仰角的关系为如图6(b)所示，摆的摆动平面始终与俯仰角为α(t)的直线(实际为弹体轴向)垂直。

根据图5所示的内筒受力分析和图6所示的简化的力学模型来建立平台内筒的动力学方程。图6中摆受到的总的力矩和M 等于摩擦力矩Mf与重力回复力矩Mg的矢量和:

式中:Mg与重力加速度g、弹体在竖直方向的加速度av(t)、摆动角度θ(t)、摆长l 和弹体俯仰角α(t)之间的关系表达式为

从(2)式中可以看出，当俯仰角α(t)为90°时，回复力矩Mg为0.

轴承的摩擦力矩Mf的SKF 表达式［9］为

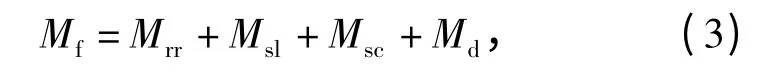
式中:Mrr为滚动摩擦力矩;Msl为滑动摩擦力矩;Msc为密封件摩擦力矩;Md为阻力损失、搅动、泼溅等的摩擦力矩。其中Mrr和Msl与弹体俯仰角的变化相关。俯仰角的变化会导致轴承轴向负荷与径向负荷发生变化，而轴向负荷变化会导致滚珠与轴承轴向接触面之间的滚动摩擦力矩和滑动摩擦力矩变化，径向负荷变化会导致滚转与轴承径向接触面的滚动摩擦力矩与径向摩擦力矩发生变化，最终导致Mrr与Msl的变化。其变化关系为:随着俯仰角的增大，Mrr和Msl的值会先增大，当俯仰角增大到一定值时，Mrr和Msl会达到最大值，此时当俯仰角再继续增大时，Mrr和Msl又会逐渐减小。

由牛顿第二定律知，外力矩沿固定轴分量的代数和等于对该轴的转动惯量与角加速度的乘积，因此总的力矩和M 还可以表示为

结合(1)式与(4)式得到

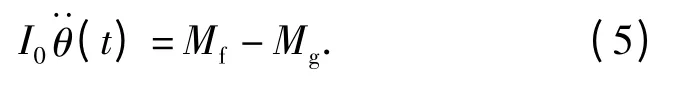
将(2)式带入(5)式得到被动式半捷联平台内筒的动力学方程:

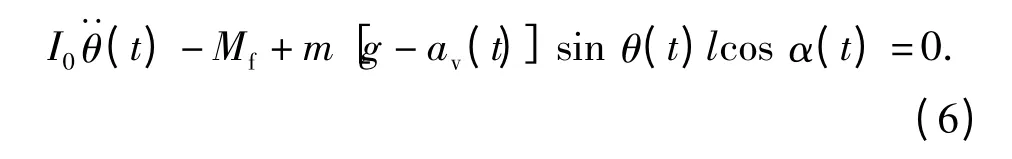
(6)式描述了被动式半捷联平台内筒转动角度θ(t)与弹体俯仰角α(t)、弹体在竖直方向的加速度av(t)、轴承的摩擦力矩Mf、平台内筒转动惯量I0、内筒质量m、重力加速度g 以及等效摆长l 之间的关系。由于(6)式为二阶齐次非线性常微分方程，无法用解析法对其进行求解，为了对平台的稳定性做进一步的研究，需要借助Matlab 用数值积分法对方程进行求解。

3 俯仰角对平台稳定性影响的计算仿真

在进行数值计算之前，需要先把(6)式简化成一阶微分方程组。引入辅助变量y1= θ(t)，y2=代入(6)式得到一阶微分方程组:

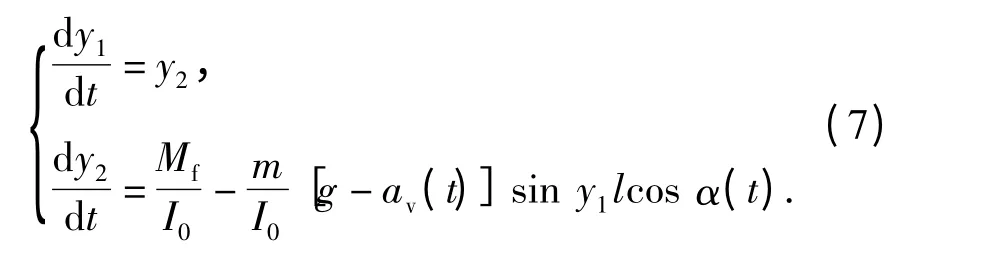
方程组(7)式中，假设下落加速度av(t)=0，g为恒定值，计算所需其他参数采用某被动式半捷联平台实验样机的实际参数，如表1所示。

表1 半捷联平台计算参数Tab.1 Parameters of partial strapdown platform

由半捷联平台内筒的力学模型可知，在俯仰角α(t)＜90°时，质量偏心可以形成复摆运动效应，因此仿真时将α(t)值分别取0°、15°、30°、45°、60°和75°，轴承摩擦力矩Mf的大小与俯仰角α(t)相关，不同α(t)对应的Mf的计算值如表2所示。

表2 不同α(t)下Mf 的计算值Tab.2 Calculated values of friction torque Mf with different α(t)

将表1和表2中的参数代入方程组(7)式中，并设初值y1(0)=0，y2(0)=0，在Matlab 中利用4 阶龙格-库塔法进行计算求解得到如图7所示的不同俯仰角下(t)和θ(t)解。

图7(a)～图7(f)分别显示了俯仰角α(t)在0° ～75°时被动式半捷联平台内筒滚转角速率(t)和角度θ(t)的时间曲线。从图7(a)～图7(f)中的(t)的曲线可以看出，(t)的计算值正负对称，符合复摆的运动规律。从θ(t)的曲线可以看出，θ(t)的计算值都在正区间内，这是由于在求解方程时假定θ(t)和(t)初值为0，并且轴承摩擦力矩方向总是朝着轴承的旋转方向。从图7(a)～图7(f)中可以看出(t)和θ(t)的幅值和周期都随俯仰角α(t)的增大而增大，因此俯仰角α(t)越小，平台越稳定。

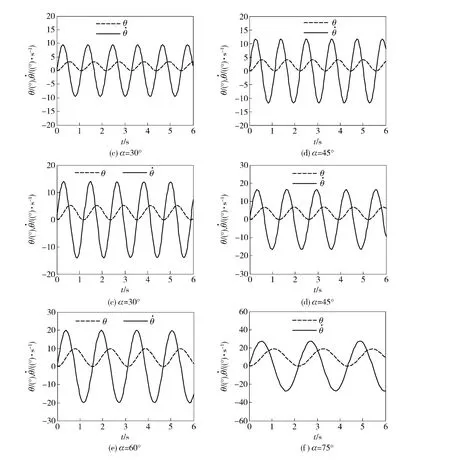
图7 仿真曲线图Fig.7 Simulation results

4 地面半实物仿真实验

为了对所建立的被动式半捷联平台的动力学模型以及图7中的计算结果进行验证，在三轴高速转台上对被动式半捷联平台样机进行了地面半实物仿真实验。用转台在滚转方向的高速旋转模拟弹体的高速滚转，转台在俯仰方向的变化模拟弹体的俯仰角变化。将被动式半捷联平台样机安装在转台内部，通过安装在平台内筒的角速率传感器测量得到内筒的摆动角速率(t)值，同时通过积分得到摆动角度θ(t)值。

设置转台滚转方向保持10 r/s 的高转速，俯仰方向分别设置在0°、15°、30°、45°、60°和75°. 实验情况如图8所示，实验得到平台内筒的摆动角速率(t)和角度θ(t)的曲线图如图9所示。

图8 高速转台实验Fig.8 Experiment on the high-speed turntable

图9(a)～图9(f)分别为转台俯仰方向设置在0° ～75°时被动式半捷联平台内筒的摆动角速率(t)和角度θ(t)的实测曲线。从图9(a)～图9(f)可以看出，平台内筒在做复摆摆动运动，且摆动角速率(t)与角度θ(t)随着俯仰角的增大而增大。将图9中的实验结果与图7中的仿真结果进行对比，转台实验结果与仿真计算结果中角速率(t)和角度θ(t)波形周期的差别不明显，并且波形幅值随俯仰角的增大而增大的规律也相符。但由于实验所用的被动式半捷联平台样机存在一定的机械加工误差，以及转台与平台之间存在一定的安装误差，导致实验结果与计算结果也存在一些差别，比如图9(a)中角速率波形的第二个波峰、图9(d)中角速率波形的第一、二个波峰以及图9(f)中角速率波形的第一个波谷都存在一定的抖动，这是由于受到机械误差和转台震动影响轴承摩擦力矩瞬间发生跳变造成的。另外图9(e)和图9(f)中角速率曲线分别出现了两个峰值相差较大的情况，产生这个变化的主要是因为随着俯仰角的增大，轴承的启动扭矩变大，而轴承启动扭矩的变大导致轴承在从静止到转动的过程中所需克服的静摩擦力矩增大。当轴承开始正常转动后，轴承摩擦力矩恢复为正常的Mf，从而使后面的角速率曲线又恢复正常。总体上转台实验曲线结果与计算求解曲线结果规律相吻合，验证了所建立的平台动力学模型，得出俯仰角越小，被动式半捷联平台越稳定的规律。

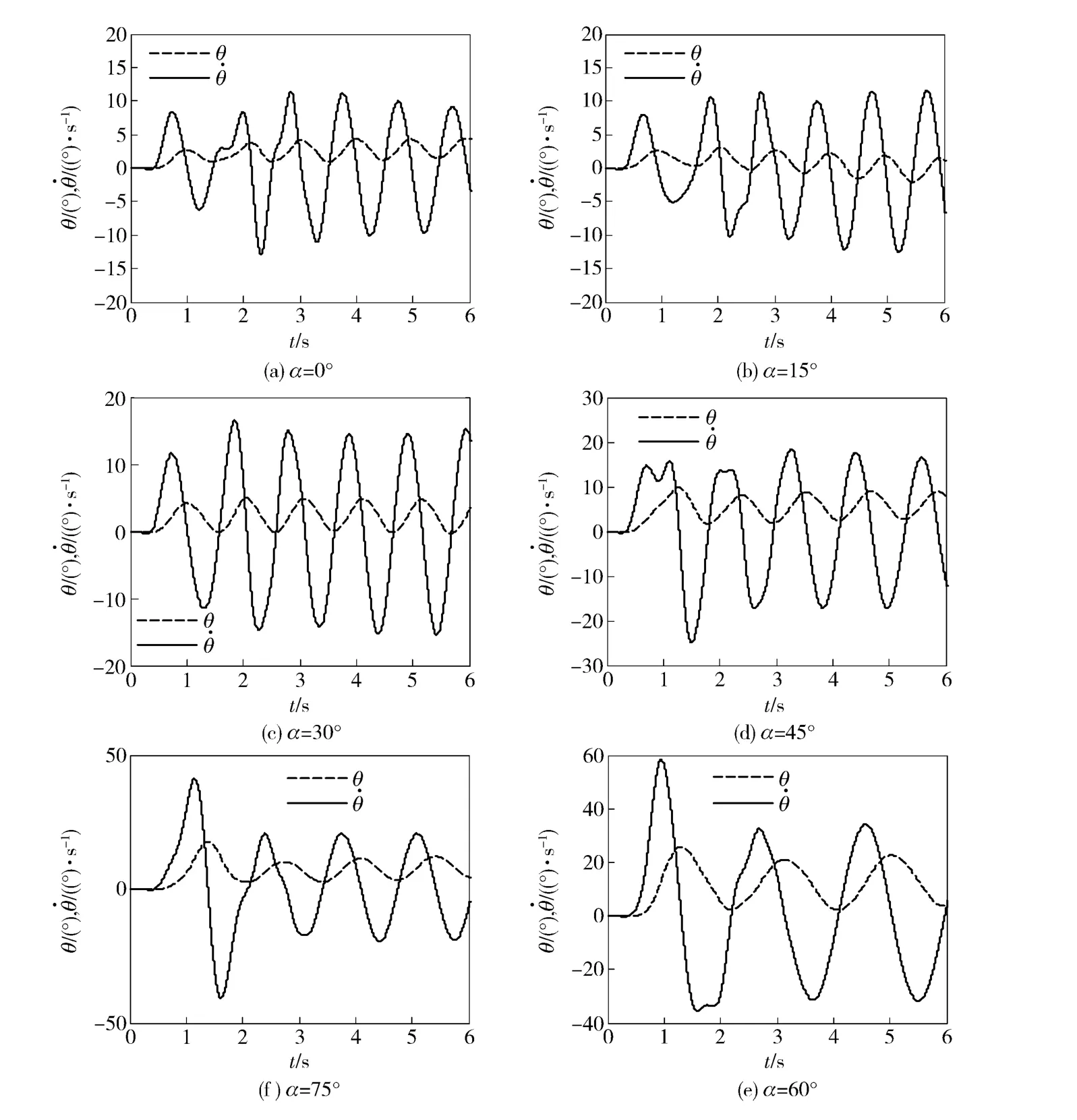
图9 高速转台实验结果Fig.9 Test results of the high-speed turntable

5 结论

本文介绍了一种适用于高速滚转制导炮弹的被动式半捷联平台。通过对弹体及平台进行力学分析，建立了半捷联平台内筒的动力学模型，通过数值计算得出了不同弹体俯仰角下半捷联式平台内筒的滚动角度和角速率，并在三轴高速转台上进行了半实物仿真实验验证。转台实验结果与仿真结果都说明弹体俯仰角的大小对半捷联式平台有直接的影响，弹体俯仰角越小，半捷联式平台越稳定。本研究对被动式半捷联平台的适用条件研究做出了一定的理论贡献，对于解决制导炮弹上惯性测量系统的应用问题具有一定的指导意义。

References)

［1］ Velde E V，Bentley G K，Fagan J H，et al. Onboard computer requirements for navigation of a spinning and maneuvering vehicle［C］∥AIAA Guidance，Control，and Fight Dynamics Conference.Pasadena，California:AIAA，1968:1 -13.

［2］ Garg S C，Morrow L D，Mamen R. Strapdown navigation technology:a literature survey ［J］. Journal of Guidance and Control，1978，1(3):161 -172.

［3］ Imbault J J，Tjulin H，Kinney R，et al. Mini-RIMS:a miniature roll-stabilized inertial measurement system［C］∥7th Conference on Sounding Rockets，Balloons and Related Space Systems. Ocean City，Maryland:AIAA，1986:35 -43.

［4］ 王晨，董景新，高宗耀，等. 火箭弹大动态单轴平台惯导系统姿态算法［J］. 中国惯性技术学报，2012，20(3):257 -261.WANG Chen，DONG Jing-xin，GAO Zong-yao，et al. Attitude algorithm of high dynamic range single-axis platform INS on rocket projectile［J］. Journal of Chinese Inertial Technology，2012，20(3):254 -261. (in Chinese)

［5］ Ohlmeyer E J，Fraysse J W，Pepitone T R. Guidance，navigation and control without gyros:a gun-launched munition concept［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit. Monterey，California:AIAA，2002:1 -14.

［6］ Davis B S. Using low-cost MEMS accelerometers and gyroscopes as strapdown IMUs on rolling projectiles［C］∥Proceeding of Position Location and Navigation Symposium，IEEE. California:IEEE，1998:594 -601.

［7］ 刘朝华，王勇，毛玉良，等. 基于MEMS 加速度计的弹体滚转角测量方法［J］. 中国惯性技术学报，2012，20(5):505 -509.LIU Zhao-huo，WANG Yong，MAO Yu-liang，et al. Measurement method of projectile's roll angle based on MEMS accelerometers［J］. Journal of Chinese Inertial Technology，2012，20(5):505 -509. (in Chinese)

［8］ 李枚，代刚，唐海林，等. 一种高动态使用微惯性测量单元的实现［J］. 中国惯性技术学报，2012，20(2):127 -130.LI Mei，DAI Gang，TANG Hai-lin，et al. Realization of micro inertial measurement unit used in high dynamic environment［J］.Journal of Chinese Inertial Technology，2012，20(2):127 -130.(in Chinese)

［9］ SKF. The SKF model for calculating the frictional moment［EB/OL］. ［2013-12-20］. http:∥www. skf. com/group/products/bearings-units-housings/ball-bearings/principles/friction/skf-model/index. html?WT. oss = Frictional% 20moment＆WT. z_oss_boost=0＆tabname=All＆WT.z_oss_rank=1.