检测与诊断齿轮裂纹故障的一种方法
陈汉新,刘 岑,杨诗琪
武汉工程大学机电工程学院,湖北 武汉430205
0 引 言
齿轮的作用主要体现在齿轮箱传递动力和连接的过程中,齿轮箱的故障诊断是对其中的零部件进行诊断,例如齿轮、转子和滚动轴承.根据统计,由齿轮问题引起的故障占到机械传动中所发生的故障至少有60%,因此对齿轮箱中的齿轮进行故障诊断的深入研究势在必行.
粒子滤波是在20世纪90年代出现的滤波计算方法[1],他主要是通过利用随机的样本来对概率分布加以描述,其中被描述的样本就叫做“粒子”,再根据测量情况,适当调整每个粒子其权值的数据以及每个样本的具体方位,来近似实际概率分布.Merwe[2]等提出了无迹粒子滤波算法,但实时性不佳;文献[3]在粒子滤波方法中引入径向基函数网络(RBFN)学习方法,即在采样的时候对粒子集中的所有粒子聚类,及时更新粒子状态,提高先验概率密度分布估计精度,消除犹豫过程噪声引起的误差,将粒子滤波的性能提高.
Wald[4]在1947年提出了序贯概率比检验算法,近年来,该检验方法在故障诊断方面有了广泛的运用,但在齿轮箱故障诊断时必须要事先确定好样本的数目.从文献[5]中可知序贯概率比检验算法比传统抽样检测所需要的样本量更少.由文献[6-7]可以知道在所有故障模式中,齿轮裂纹最易模拟,因此选择齿轮裂纹来进行诊断分析是可行的,但是实验中得到的信号不仅包括有用信号同时还夹杂着噪声等干扰,影响了系统的稳定性.
基于参数序贯概率比检验的齿轮裂纹故障诊断方法,是将每个假设检验数据与设定值进行比较,具有不预先规定观测样本群数量的优点;因此,文中提出的将RBF网络优化的粒子滤波与序贯概率比检验相结合的方法,即首先运用RBF网络优化粒子滤波算法对信号进行降噪处理,获得稳定信号;然后采用对冲击性振动极其敏锐的峭度值作为特征参数,利用时域分析法来处理对信号加以降噪处理之后的特征数值;最后利用序贯概率比检验算法来分析齿轮裂纹的故障.实验研究表明,文中提出的方法对齿轮裂纹故障诊断是有效与可靠的.
1 RBF网络优化的粒子滤波原理
RBF网络优化的粒子滤波原理就是利用径向基函数网络能以任意精度逼近任意连续函数的性能来优化粒子滤波的采样过程.通过RBFN对初始化后的目标状态进行完整性的全局估计,利用径向基函数神经网络学习算法更新各粒子状态,从而获取新的重要性权值.基本步骤如下:

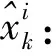
步骤5:输出.得到更新后的状态估计.
2 序贯概率比检验原理
文献[8]中序贯概率比检验算法可总结为:设x1,x2,…为一组满足独立同分布的随机变量序列.xi在这里代表的是样本集{xi}中任意的观察数值,假设{xi}是离散型随机变量,其条件概率分布假定为f(x/θ),其中,{xi}之分布由θ确定.
就二元变量序贯概率比检验而言,初假设是H0∶θ=θ0,备择假设是H1∶θ=θ1.
它们的联合分布密度函数为:
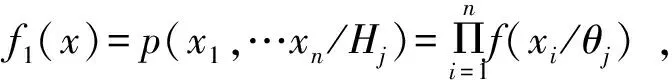
序贯概率比检验的似比λ为:
λn(x)=λn(x1,…,xn)=
依照假设检验里面的一类错误概率α以及二类概率β得出阈值A与B(A>B).在这里x1为集合里面的首个观察数值,把它代进上一个公式里面求出似然比,即λ1(x1).之后同之前设置的阈值加以对比,最终判断故障模式.如果似然比满足:
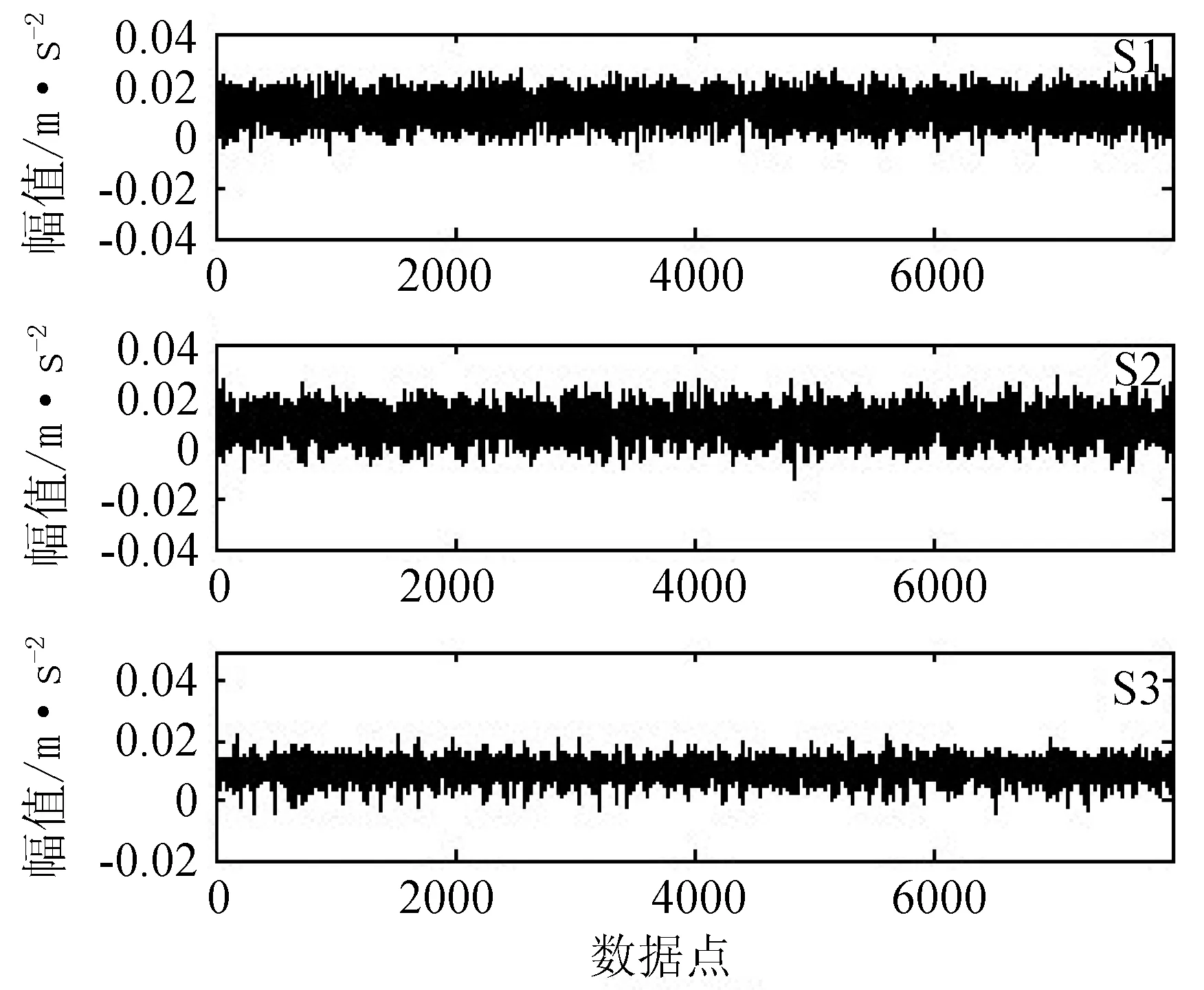
λ1(x1) 则终止检测,按照初假设H0处理,放弃H1;如果似然比满足: λ1(x1)>A 依然终止抽样,拒绝初假设H0同时接受备择假设H1;如果似然比为: B≤λ1(x1)≤A 接着使用下一个观察数值求出似然比λ2(x1,x2).假如似然比符合λ2(x1,x2) 整个系统允许出现的错误概率α与β直接确定检验当中的主要的边界常数A、B.α、β同A、B两个常数有着以下的密切联系: 为检验所设计的新检测方法对于故障的确定是否有效,模拟了齿轮箱振动实验,这里有三种情况组成,分别为非故障情况下的F1与故障情况下的F2、F3.所谓的非故障就是不存在裂纹,用F1代表;故障情况的是用F2与F3代表,亦即存在裂纹.在这里的F2代表裂纹的深度和宽度分别是裂纹全深度和全宽度的25%,而F3代表的裂纹分别为全深度和全宽度的50%.其中裂纹全深度a为2.4 mm,是弦齿厚度的的50%,裂纹全宽度b为25 mm,厚度是0.4 m,压力角均为45°.将齿轮箱设定为空载状态下运行,转速为800 r/min,设定的三个故障情况如表1所示. 表1 三种故障模式 图1表示齿轮箱工作结构,齿轮3、4由于冲击力会导致振动,可任意选择其一来对故障情况进行模拟.本实验中选取齿轮3来模拟. 把2个加速传感器装到齿轮箱水平垂直方向,利用动态模拟器收集它的振动信号,应用频谱分析仪,对收集到的信号数据加以传输存储.本文仅就水平方向的信号加以处理分析,其中,使用S1代表非故障情况下的信号,S2表示25%裂纹齿轮下采集到的振动信号,而S3表示50%裂纹齿轮下采集到的原始振动信号. 图1 齿轮箱工作结构图 通过RBFN的优化,各粒子状态更新将趋向于真实状态,更加符合实际情况.同时也提高了对目标状态的概率分布估计精度,减少了粒子更新过程中误差累计对状态估计的影响.它不再利用固定的状态方程更新目标状态,而是根据对目标状态预测的实际需要,通过前若干时刻测量值的干预,避免粒子状态估计受到积累误差的影响,增强粒子状态估计过程的适应能力,从而获得更细致、准确的平稳信号,用以序贯概率比检验. 特征参数能够反映振动信号的特征信息,将原始振动信号进行优化粒子滤波降噪得到接近真实值的数据集合,再从中提取相关特征参数,实验中的离散待检信号xi=[x1,x2,…,xN] ,N=8 192,每组取1 024个检验点,这样就可以得到7 169组检验数据.能够使用下列方式就算出不同的参数. 峭度值集合ki=[k1,…,kn]是研究中需要的离散检验信号,其均值和标准差分别为: 峭度值对于振动信号非常敏锐,因此序贯概率比检验参数选择峭度值来进行计算. 通过似然比计算发现,方差以及平均值对其结果有很大的影响.通过RBF优化粒子滤波降噪,发现提取出的振动真实值序列符合高斯分布.当齿轮箱为正常状态时,这一信号序列符合初假设H0:μ=μ0;当处于故障情况时,这一信号序列符合备择假设H1:μ=μ1.其标准差σ不发生变化,均值产生变动,如果上述两个假设都能成立,那么这一序列联合密度如下. 式中,p0i表示初假设条件下的概率密度函数,p1i表示备择假设条件下的概率密度函数.其似然比能够用下面式子进行表示: 其中,p0为初假设条件下的先验概率,p1为备择假设条件下的先验概率.在现实处理时,应当把公式作如下处理,从而使得计算更精确简便. 此时,阈值a=lnA,b=lnB. 假如似然比符合Δ 图3是正常模式以及两种故障模式下所采集到的原始振动信号.其中S1为正常模式,S2表示裂纹为25%的齿轮振动信号,S3为50%的裂纹齿轮振动信号.将上述信号输入滤波运算程序,即用RBF优化粒子滤波去噪,得到最终的稳定信号,如图4所示. 峭度值对振动信号反应非常敏锐,其均值的变化对于检验时间、精确性及似然比影响甚大.假设H0与H1两种情况下其对应的犯第一类错误和第二类错误概率是一致的,取α=β=0.005,同时确定观测所得的信号的先验概率一致. 图2 序贯概率比检验流程图 图3 实验中得到的三组振动信号 通过似然比计算公式可知,均值的偏差对于计算结果Δ的影响很大.非故障情况信号S1的平均值记为参数μ0,故障情况S2与S3的平均值记为参数μ1,检验其信号,可得到图5. S1的平均值记为μ0,S2的平均值记为μ1,代入似然比公式计算,得到图5(a).从图5(a)可知,将真实振动序列S1输入序贯检验程序时,计算结果满足Δ 图4 RBF优化粒子滤波去噪后的振动信号 (a) (b) 值得注意的是,对不同程度的齿轮裂纹信号也可以运用序贯概率比检验算法进行区分.对于S2与S3,将S2的平均值记为μ0,将S3的平均值记为μ1,构建检验模加以计算,可得到图6. 图6 序贯概率比检验结果 由图6可知,将S2的均值记为参数μ0,S3的均值记为μ1,将信号S2输入似然比计算程序时,计算结果满足Δ 基于RBF网络优化的粒子滤波降噪与序贯概率比检验相结合的原理,提出了一种对齿轮箱故障进行诊断与检测的方法.将正常齿轮和两种故障齿轮的状态进行对比,最终识别不同齿轮箱状态,证实文中提出的方法能有效可靠地对齿轮进行故障的分析与诊断;研究成果可供复杂旋转机械的故障检测与诊断参考. 致 谢 感谢国家自然科学基金(61273176),教育部新世纪优秀人才支持计划(201010621237),湖北省教育厅科学技术研究重大项目(Z20101501)和教育部留学回国人员科研启动基金(20091001)对本研究的资助. [1] GORDON N J, SALMOND D J, SMITH A F M . A novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings on Radar and Signal Processing, 1993, 140(2): 107-113. [2] MERWE R V, DOUCET A, FREITAS N D,et al. The unscented particle filter[R]. Technical Report CUED/F-INPENG/TR 380, Cambridge University Engineering Department, 2000. [3] CHEN Hanxin, TU Ling, SUN Kui, et al. Noise reduction method based on RBF network optimized particle filter[C]//Key Engineering Materials Vols,(589-590)2014:629-633. [4] WALD A. Sequential Analysis[M]. New York: Wiley,1947. [5] WALD A. Sequential tests of statistical hypotheses[J]. Ann. Math. Statist. 1945, 16(2): 117-186. [6] STANDER C J, HEYNS P S, SCHOOMBIE W. Using vibration monitoring for local fault detection on gears operating under fluctuating local conditions[J]. Mechanical Systems and Signal Processing. 2002, 16(6):1005-1024. [7] FAKHFAKH T, CHAARI F, HADDER M. Numerical and Experimental Analysis of a Gear System with Teeth Defects[J]. International Journal of Advanced Manufacturing Technology, 2005, 25(5-6):542-550. [8] YU Chenggang, SU Bingjing, A non-parametric sequential rank-sum probability ratio test method for binary hypothesis testing[J]. Signal Processing, 2004(84): 1267-1272.3 齿轮箱故障诊断试验
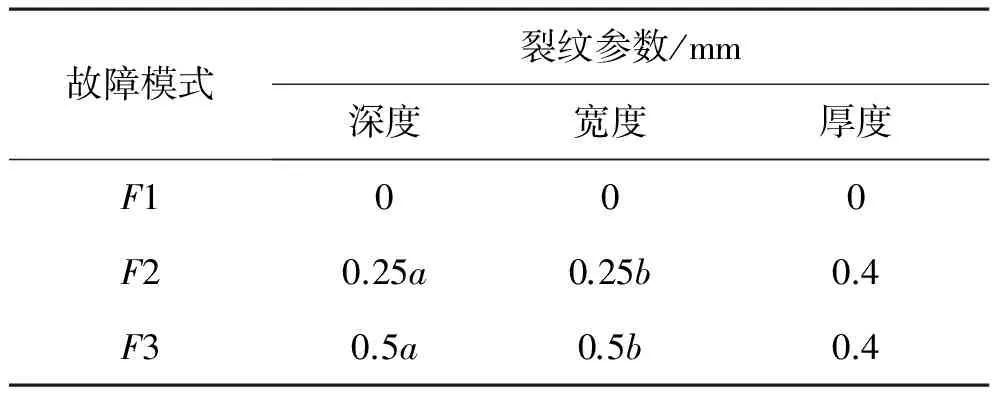

4 齿轮裂纹的序贯概率比检验
4.1 RBF网络优化粒子滤波降噪
4.2 特征参数提取
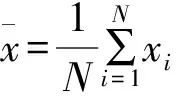
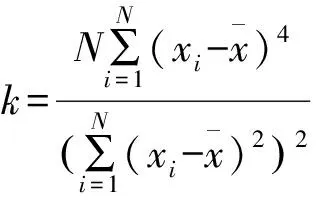
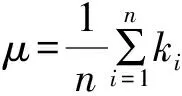

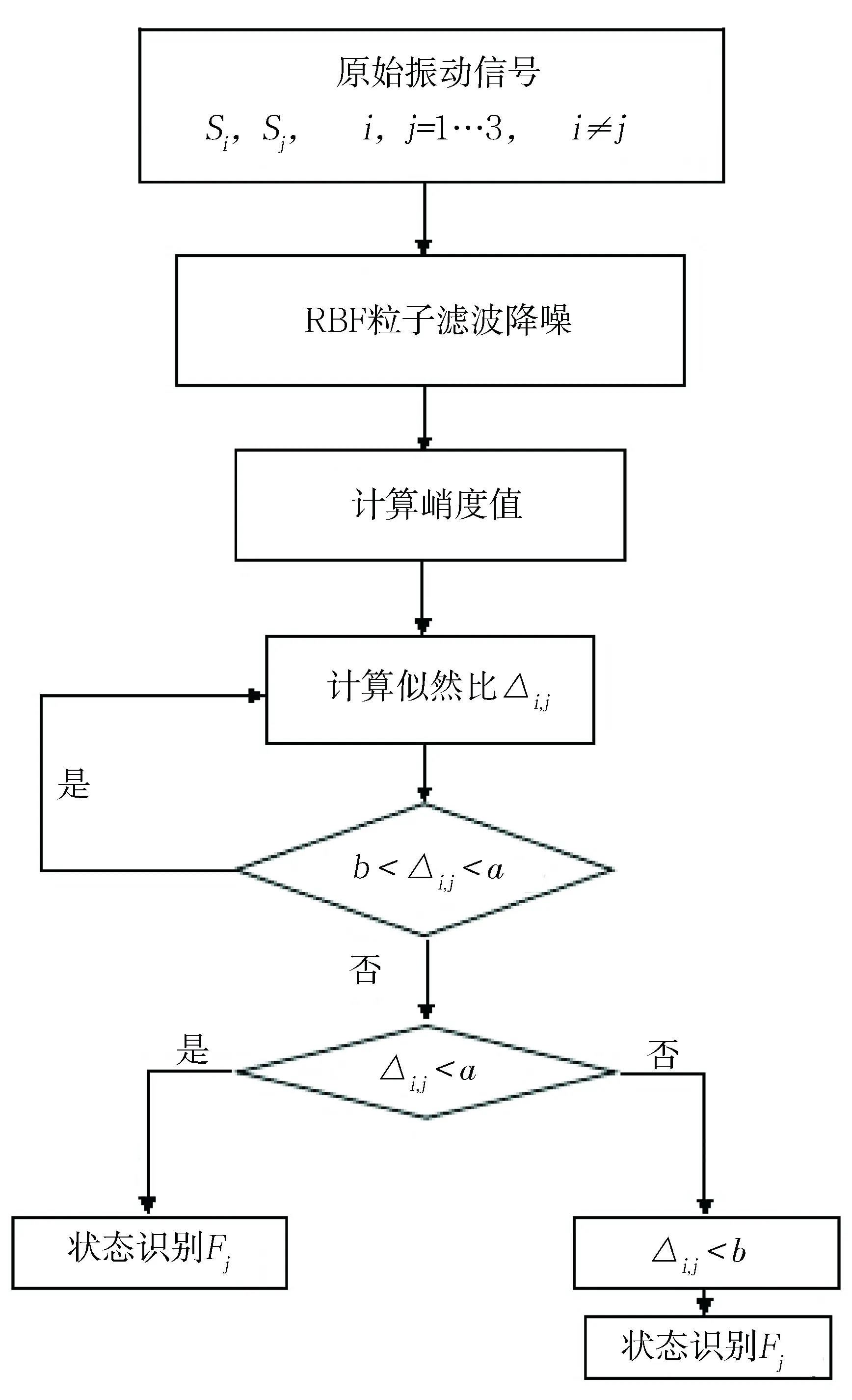
4.3 Wald序贯检验
5 结果与分析




6 结 语

