辐射松和稻壳及其三组分热重动力学

王 昶，张征标，柏龙佳，郝庆兰

(1. 天津科技大学海洋科学与工程学院，天津 300457；2. 天津科技大学材料科学与化学工程学院，天津 300457)

辐射松和稻壳及其三组分热重动力学

王 昶1，张征标2，柏龙佳1，郝庆兰2

(1. 天津科技大学海洋科学与工程学院，天津 300457；2. 天津科技大学材料科学与化学工程学院，天津 300457)

利用热天平对两种植物生物质(辐射松和稻壳)及其三组分半纤维素、纤维素和木质素分别在不同的升温速率下进行热重分析，调查这些样品随热解温度的失重情况以及热解动力学．随着升温速率的增加，半纤维素的DTG曲线表现出不同于其他实验样品的规律，即DTG曲线的峰值向低温区移动．使用Kissinger微分法、FWO法和Popescu法联合对热解数据进行分析，分别计算反应活化能E和指前因子A，以及最可几机理函数，其中Jander方程为纤维素、辐射松和稻壳的最可几机理函数，反Jander方程为半纤维素和木质素的最可几机理函数，可以较好地解决植物生物质及其三组分的动力学参数的求算．

生物质；动力学；纤维素；半纤维素；木质素

纤维素、半纤维素和木质素是构成植物生物质的3种主要组分，植物生物质还含有脂肪、蛋白质和水分，生物质热裂解可认为是以上各组分热裂解行为的综合表现[1–2]．热重分析是研究物质热裂解过程的重要工具，也是研究物质热解动力学的重要手段．许多学者对生物质热重动力学进行研究：周利民等[3]将生物质和塑料热解的共热解反应假设为一级反应后运用Coats-Red-fem积分法进行动力学分析，得到混合样3个线性段的活化能(E)分别为107～128,kJ/mol、164～249,kJ/mol、426～498,kJ/mol．虽然Coats-Redfem积分法是很多学者进行动力学分析时选取的方法[4–6]，但该法在推导过程中首先要假定反应级数，同时引入积分近似，因此，动力学计算结果会产生一定误差，且所得活化能较低．曾凡阳等[7]运用FWO法对不同分解转化率下黄桷树的活化能进行计算，黄桷树热解活化能随着反应的深入呈增大趋势，得到参考活化能为224.3,kJ/mol．虽然该方法可以较准确地计算活化能，却不利于其他动力学参数的计算．除采用单一方法外，宋春财等[8]采用4种方法：Coats-Redfem积分法、Doyle法、最大速率法(Kissinger微分法)和分布活化能模型(DAEM)对玉米秸秆和稻秆热失重动力学参数进行计算，Doyle法和DAEM模型计算得到的活化能接近，都在170～220,kJ/mol内变化，通过对比分析发现不同方法得出的结果不同．然而，针对不同方法的特点，结合几种动力学方程分别计算动力学参数的研究却鲜见报道．

本文对构成生物质的三大组分(纤维素、半纤维素和木质素)以及植物生物质(稻壳和辐射松)在不同的升温速率下进行了热重分析．根据不同方法的特点进行了较合理的求算，先运用Kissinger微分法对活化能进行估算，再运用FWO法对活化能值进行较准确地计算，最后利用Popescu法选取最可几机理函数并求算指前因子(A)．

1 材料与方法

1.1 原料

实验用生物质为2007年天津蓟县水稻稻壳和辐射松．生物质风干后经粉碎、筛分，选取粒径在100～120目的颗粒，热重实验前在105℃恒温干燥2h．微晶纤维素(粒径约为100μm，质量分数97%)、半纤维素(质量分数85%)、木质素(造纸纸浆中提取，日本进口)，上海源叶生物科技公司．实验用生物质的干燥无灰基化学组成见表1，实验样品的干燥无灰基工业分析见表2．

表1 生物质样品的化学组成Tab. 1 Chemical composition of biomass samples

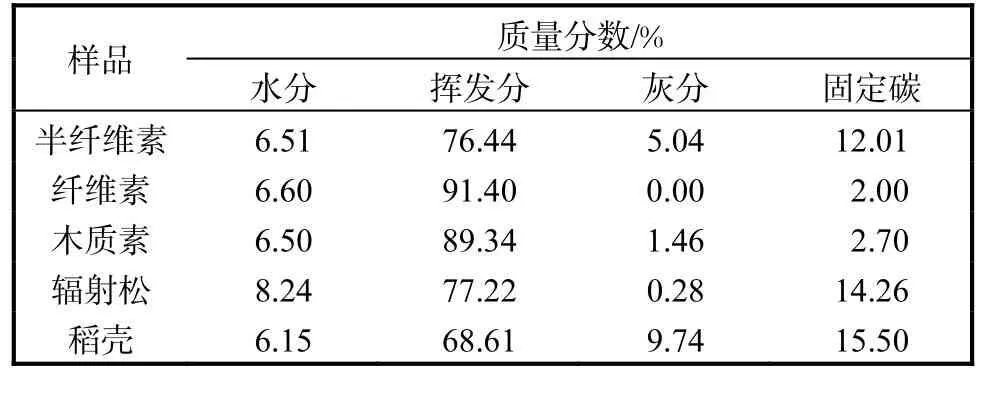
表2 实验样品的工业分析Tab. 2 Proximate analyses of experimental samples

1.2 热重分析

热重分析采用美国TA公司生产的Q50型热重分析仪，原料用量为每次10mg，放置于金属铂盘中，在40mL/min的高纯氮气气氛中分别以10、20、30、40℃/min的升温速率由室温升温至900℃．

2 结果与讨论

2.1 实验样品的热重实验

30℃/min升温速率下实验样品的TG曲线如图1所示．由图1可知，虽然温度区间不同，但随着温度的升高，实验样品热解过程中都有4个明显的阶段．第1阶段为失去内部结晶水的过程，第2阶段的曲线较为平稳，在该阶段实验样品内部发生少量解聚和“玻璃化转化”过程[9]；第3阶段为热解的主反应阶段，试样的大部分失重发生在该阶段，最后阶段是残留物缓慢分解的过程．在构成生物质的3大组分中，纤维素的热稳定性最高且失重第3阶段温度区间最小，热解完全后固体残留物最少；木质素固体残留物最多且失重温度区间跨度最大，这与其复杂的结构有关，分解行为表现为多个过程的竞争反应[10]；半纤维素热稳定性最差，进入主反应阶段的温度最低．辐射松与稻壳相比较，两种生物质主反应阶段温度区间分别为200～420℃和240～390℃，辐射松固体残留物为15.5%低于稻壳的27.5%，这与不同生物质的化学组成及结构有关．

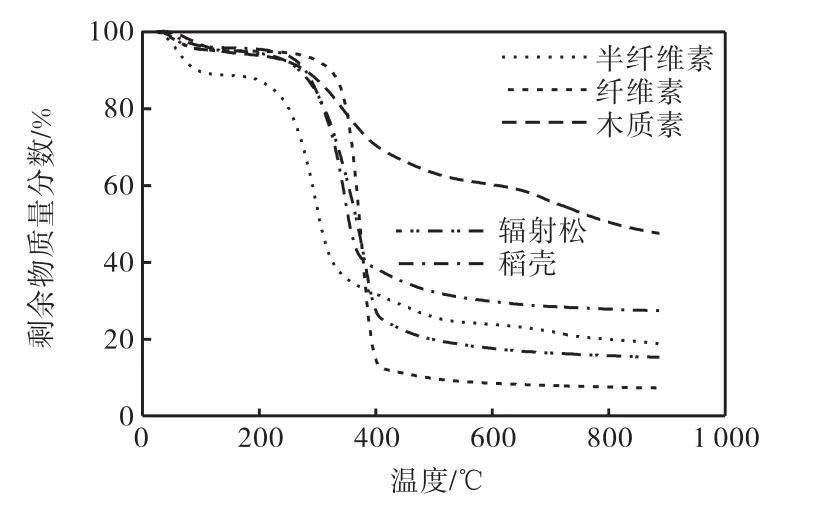
图1 实验样品在30℃/min升温速率下的TG曲线Fig. 1 TG curves of samples under 30℃/min heating rate

图2为辐射松在不同升温速率下的TG和DTG曲线．由图2可以看出，随着升温速率的升高，热失重曲线向高温侧移动，最大失重速率也随之降低，可能是由于热分解过程中传质与传热的变化对热解反应的进行产生了影响．在所研究的5种实验样品中，只有半纤维素的热重曲线不符合此规律，随着升温速率的升高，半纤维素DTG曲线的峰值向低温区移动．这主要是由于半纤维素的热稳定性差，在较低的热解温度下就进入了主反应阶段．

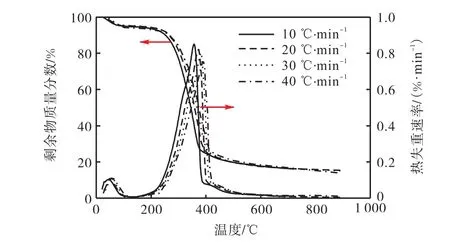
图2 辐射松在不同升温速率下的TG和DTG曲线Fig. 2 TG and DTG curves of radiata pine at different heating rates

2.2 热解动力学分析

生物质热失重的热解反应可以简化为

A(固)→B(固)＋C(气)

根据质量作用定律可以得到试样分解速率为

式中：t为反应时间；k为速率常数；α 为分解程度，可由式(2)计算得到．

式中：m0为试样初始质量；m为试样在温度为T时质量；m∞为试样热解最终质量．

由Arrhenius公式得

式中：R为气体常数，8.314,J/(mol·K)；E为表观活化能，kJ/mol；T为试样温度，K；A为指前因子，min-1．

一般假设函数f(α)与温度和时间无关，只与分解程度有关，可取n为反应级数；则有

运用不同方法对式(4)进行处理，可得到不同的数学表达式．

2.2.1 Kissinger微分法[11]

将式(4)两边微分可得[12]

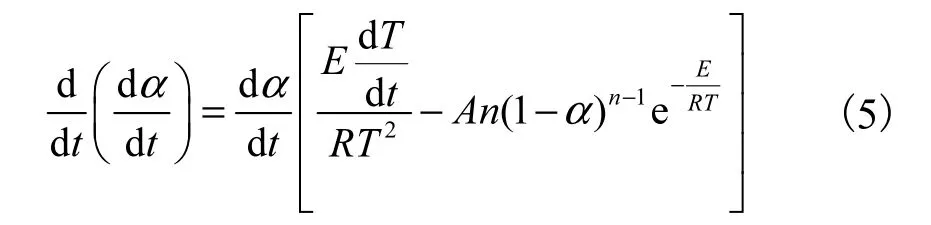
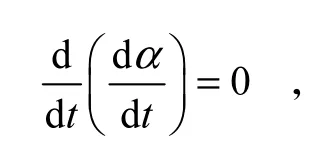
运用Kissinger微分法所得数据见表3．

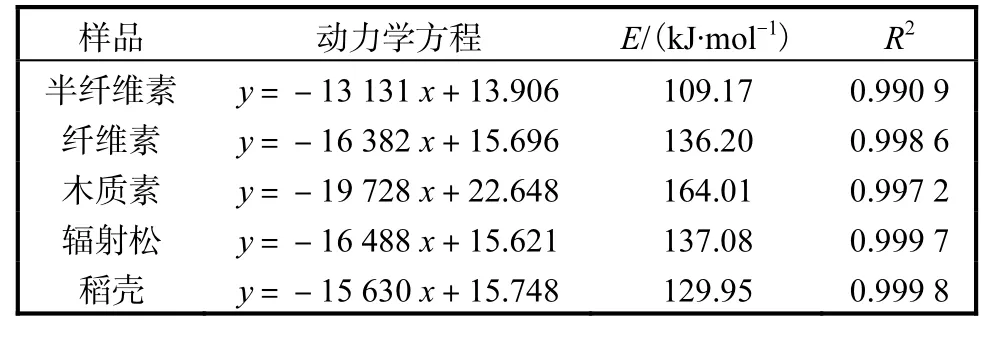
表3生物质在不同升温速率下经Kissinger方程求解的热解反应活化能Tab. 3Results of biomass pyolysis kinetics with Kissinger equation in different heating rates

Kissinger法以不同的升温速率进行多次TG扫描，对不同升温速率下的最大失重处温度值进行处理，而与其他值无关，处理工作相对简单．但该法在计算推导过程中要对机理进行假定，同时引入了积分近似，动力学计算结果会产生相应的误差．方程推导过程中进行了2RTP/E≪1的假设，但经计算，半纤维的2RTP/E范围为0.083～0.088，纤维素为0.076～0.080，木质素为0.060～0.063，辐射松为0.076～0.080，稻壳为0.076～0.080，2RTP/E不足以远小于1，因此会影响参数计算的准确性，对E进行粗略估算时，结果表现出有所偏低的趋势．

2.2.2 Flynn-Wall-Ozawa(FWO)法

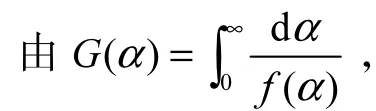
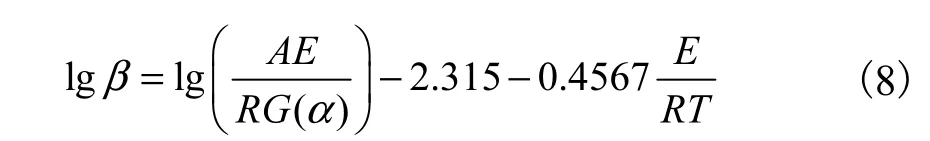
表4 辐射松和稻壳生物质的FWO方程处理结果Tab. 4 Results of radiata pine and rice husk pyolysis kinetics with FWO equation

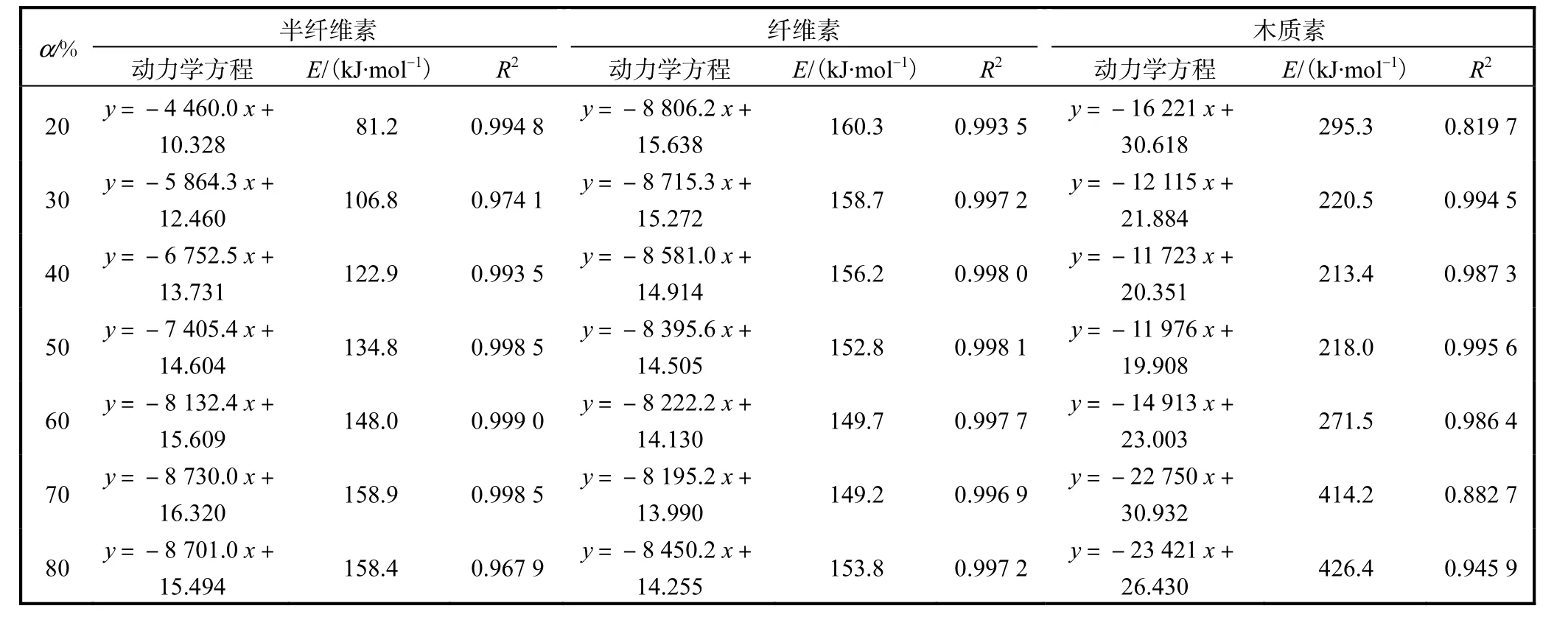
表5 生物质中半纤维素、纤维素以及木素的FWO方程处理结果Tab. 5 Results of hemicellulose，cellulose and lignin pyolysis kinetics with FWO equation

该法避开了反应机理函数的选择而直接求出活化能，与Kissinger法相比，它避免了因假设而可能带来的误差，成为许多科研工作者检验由其假设的反应机理函数是否合理的标准，这也是Ozawa法的一个突出优点[12]．

由表4和表5可知，由Ozawa法可以得到5种生物质在不同升温速率下的热解动力学活化能，随着热解温度的提高，生物质中的挥发分不断产生，依据这些物质对温度的稳定性，其不同分解程度下的活化能要比Kissinger法不同升温速率下的平均活化能更加能够反映出生物质内部挥发分的分解情况．半纤维素的活化能随着分解程度α 的增加而增大，因为半纤维素多糖的热稳定性差，易于在低温下分解．木质素在分解程度70%以上，活化能有了很大的增加，这可能是由于木质素自身就带有稳定的苯环结构，例如愈创木酚、紫丁香醇等木质素基团，经热解缩合后的固体物质具有更稳定结构，表现出难以分解的缘故．再由TG曲线可知，α 为20%～80%时，是热解变化最大区域，所以可近似将这一区域认定为热解主反应区．从整体结果来看，5种生物质的热解反应活化能值高于Kissinger法的结果，只是半纤维素在热解反应初期的反应活化能值比较低，说明半纤维素不稳定，热分解的阻力小，易于分解．

2.2.3 Popescu法[15]

上述的FWO法通过数学处理，避免了机理函数的假设，虽说能够计算出活化能，但无法对动力学方程中的指前因子A进行直接计算，为此Popescu法在不回避机理函数的情况下，优化处理，得到最可几机理函数，从而确定指前因子．

Popescu法首先对动力学积分式进行最简近似处理，得

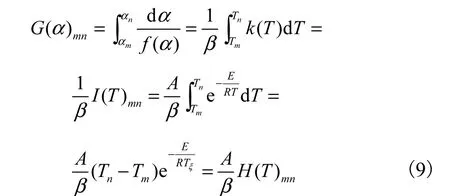
对式(9)取对数可得

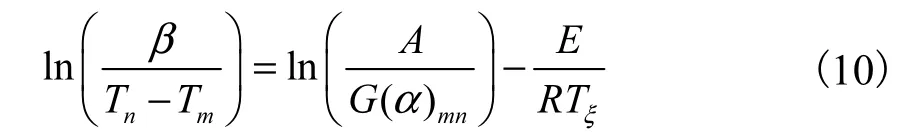
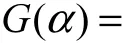
5种生物质由Popescu法计算的结果见表6，由表6可知：运用在不同升温速率下得到的数据点对机理函数进行选取时，5种生物质的热解反应活化能所拟合得到的直线方程线性相关性很好．除了木素，其他4种生物质与活化能相对应的指前因子所拟合得到的直线方程线性相关性也很好，但木素相对较差，这可能是由于木质素结构复杂，相对稳定，难以热解(图1)的缘故．所得到的5种生物质E值均在FWO法所确定的活化能范围之内，从而较好地解决了热解过程中动力学机理，获得了有用的反应活化能和相应的指前因子．

表6 实验样品的Popescu法处理结果Tab. 6 Results of sample pyolysis kinetics with Popescu method

3 结 论

(1)纤维素、辐射松、稻壳和木质素生物质的TG曲线随升温速率的增加而向高温侧移动，DTG曲线峰值随之降低，而半纤维素因热稳定性差而有所不同．纤维素、辐射松、半纤维素、稻壳和木质素的固体残留物依次增加．

(2)由FWO法避免机理函数的选择，对5种生物质的热解主反应区热解反应的活化能进行了计算，其结果：辐射松为144.5～163.8,kJ/mol，稻壳为143.9～215.9,kJ/mol，半纤维素为81.2～158.9,kJ/mol，纤维素为149.2～160.3,kJ/mol，木质素为213.4～426.4 kJ/mol．

采用Popescu法对不同的机理函数进行计算，选取出最可几机理函数G(α )，利用最可几机理函数可求算出与活化能相对应的指前因子，从而获得了热解过程中有用的动力学参数．

［1］ Orfao J J M，Antunes F J A，Figueiredo J L. Pyrolysis kinetics of lignocellulosic materials：Three independentreactions model[J]. Fuel，1999，78(3)：349–358.

［2］ 文丽华，王树荣，骆仲泱，等. 生物质的多组分热裂解动力学模型[J]. 浙江大学学报：工学版，2005，39(2)：247–252.

［3］ 周利民，王一平，黄群武，等. 生物质/塑料共热解热重分析及动力学研究[J]. 太阳能学报，2007，28(9)：979–983.

［4］ 武宏香，李海滨，赵增立. 煤与生物质热重分析及动力学研究[J]. 燃料化学学报，2009，37(5)：538–545.

［5］ 张雪，白雪峰. 几种木质类生物质的热重分析研究[J].黑龙江大学自然科学学报，2012，29(3)：352–358.

［6］ 邵千钧，彭锦星，徐群芳，等. 竹质材料热解失重行为及其动力学研究[J]. 太阳能学报，2006，27(7)：671–676.

［7］ 曾凡阳，刘朝，王文钊，等. 生物质热重实验及动力学分析[J]. 工业加热，2008，37(3)：6–8.

［8］ 宋春财，胡浩权，朱盛维，等. 生物质秸秆热重分析及几种动力学模型结果比较[J]. 燃料化学学报，2003，31(4)：311–316.

［9］ Antal M J J，Varhegyi G. Cellulose pyrolysis kinetics： The current state of knowledge[J]. Industrial & Engineering Chemistry Research，1995，34(3)：703–717.

［10］ 谭洪，王树荣，骆仲泱，等. 生物质三组分热裂解行为的对比研究[J]. 燃料化学学报，2006，34(1)：61–65.

［11］ Kissinger H E. Reaction kinetics in differential thermal analysis[J]. Analytical Chemistry，1957，29(11)：1702–1706.

［12］ 胡荣祖，史启祯. 热分析动力学[M]. 北京：科学出版社，2001：65–146.

［13］ Flynn J H，Wall L A. A quick，direct method for the determination of activation energy from thermogravimetric data[J]. Journal of Polymer Science Part B：Polymer Letters，1966，4(5)：323–328.

［14］ Ozawa T. Kinetic analysis of derivative curves in thermal analysis[J]. Journal of Thermal Analysis and Calorimetry，1970，2(3)：301–324.

［15］ Popescu C. Integral method to analyze the kinetics of heterogeneous reactions under non-isothermal conditions A variant on the Ozawa-Flynn-Wall method[J]. Thermochimica Acta，1996，285(2)：309–323.

责任编辑：周建军

Thermogravimetric Dynamics of Radiata Pine，Rice Husk and their Three Biomass Componens

WANG Chang1，ZHANG Zhengbiao2，BAI Longjia1，HAO Qinglan2
(1. College of Marine Science and Engineering，Tianjin University of Science & Technology，Tianjin 300457，China；
2. College of Material Science and Chemical Engineering，Tianjin University of Science & Technology，Tianjin 300457，China)

Different pyrolysis characteristics of wood biomass(radiata pine and rice husk)and their three biomass componens(hemicellulose，cellulose and lignin)at different heating rates were studied with TG. The DTG curves of the hemicellulose was different from other samples，and they moved towards the low temperature region with the increase of heating rate. Three methods，Kissinger，FWO and Popescu，were used to determine the kinetics. Based on the characteristics of different methods，the pre-exponential factor，activation energies and most probable mechanism functions of the five samples were detemined. The most probable mechanical functions of cellulose，pinups radiate and rice husk were Jander equation：while others were anti Jander equation：The kinetic paramenters of the five samples could be solved well by using the three methods in combination.

biomass；kinetics；cellulose；hemicellulose；lignin

TQ351.2

A

1672-6510(2014)01-0030-06

10.13364/j.issn.1672-6510.2014.01.007

2013–07–01；

2013–08–26

国家自然科学基金资助项目(21176191)

王 昶（1958—），男，江苏人，教授，wangc88@163.com.