长江流域和淮河流域年径流丰枯遭遇分析

张 荣花加凤丁 兵

（1.江苏省盐城市水利勘测设计研究院 盐城 224000 2.长江科学院河流研究所 武汉 430010）

长江流域和淮河流域年径流丰枯遭遇分析

张 荣1花加凤1丁 兵2

（1.江苏省盐城市水利勘测设计研究院 盐城 224000 2.长江科学院河流研究所 武汉 430010）

本文运用Copula理论构造了长江流域大通站和淮河流域鲁台子站年径流联合分布，并用所建模型定量描述了长江和淮河流域年径流丰枯遭遇的概率。结果表明，应用Copula方法来描述不同地区径流丰枯变化是可行的。通过分析可知，长江流域和淮河流域同为丰水年的概率为20.6%；同为枯水年19.4%；长江流域为丰水年的概率为37.7%；长江流域为丰水年，淮河流域为枯水年的概率为8.5%。可见，长江流域和淮河流域年径流具有丰枯补偿特性，可以相机从长江流域向淮河流域调水。

长江流域 淮河流域 年径流 Copula理论

一、引言

径流丰枯遭遇分析对研究径流补偿特性具有重要的意义。郑红星等根据同步水文系列进行经验频率计算，确定南水北调东、中两线不同水文区降水丰枯的遭遇概率，但该法没有考虑水源区与受水区之间大气降雨的内在联系，理论上尚待完善。戴昌军和梁忠民通过统计试验对正态变换等3种联合分布计算方法进行比较研究，并用正态变换的Mom法分析了南水北调东线径流丰枯遭遇频率。该法计算比较复杂，且在数据转换过程中难免会使一些信息失真。闫宝伟等运用Copula方法理论构造了南水北调中线工程水源区与各受水区汛期、非汛期及各年降雨量的联合分布，并用所建模型对水源区与各受水区的丰枯遭遇进行了研究。

本文采用Copula方法对长江流域大通站和淮河流域鲁台子站年径流的丰枯遭遇进行研究，选取1956～1991年共36年年径流系列，通过Copula函数构造两站年径流的联合分布，定量分析两站的径流丰枯遭遇概率。

二、基于Copula理论的联合分布

Sklar定理：设X、Y为连续的随机变量，边缘分布函数为FX、FY，F（x，y）为变量X、Y的联合分布函数，如果FX、FY连续，则存在唯一函数Cθ（u，v）使得：

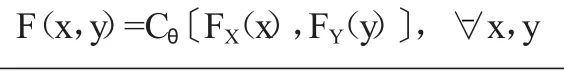
式中：Cθ（u，v）为Copula函数，θ为待定参数。

3种比较常用的阿基米德Copula函数及参数θ的范围如下：

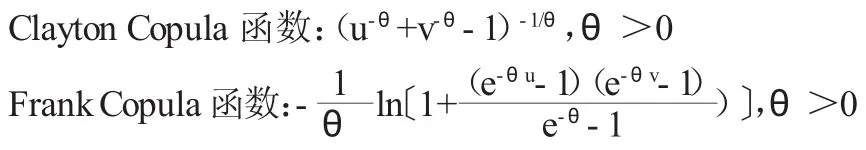
GumbelCopula函数：exp{-〔（-lnu）1/θ+（-lnv）1/θ〕θ}，0≤θ≤1

基于Copula理论联合分布的建立，一个完整的水文事件一般包含多个水文变量，而多个变量间往往存在一定的相关性，Copula理论正是通过构造联合分布来描述这种相关结构的。具体应用包括以下几个步骤：（1）确定各水文变量的边缘分布；（2）构建联合分布的似然最大函数，采用加速遗传算法率定参数θ；（3）根据评价指标选择Copula函数，建立联合分布；（4）根据所建分布进行相应分析。

三、联合分布模型的建立

1.边际分布函数的选定

我国水文分析中一般假定洪量服从P—Ⅲ分布，其概率密度函数为：

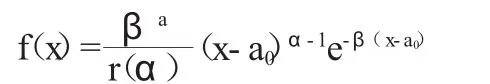
其中：r（α）为伽玛函数；α、β、a0分别为形状、尺度和位置参数。可以推证三者与常用统计参数x、CV、CS之间的关系：

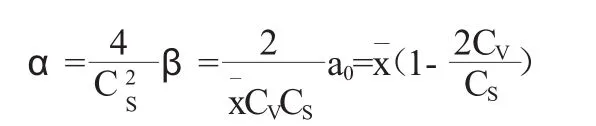
文中采用线性矩法估计上述参数，并根据目估适线作适当的调整，可得到大通站和鲁台子站年径流的常用统计特征参数，见表1。

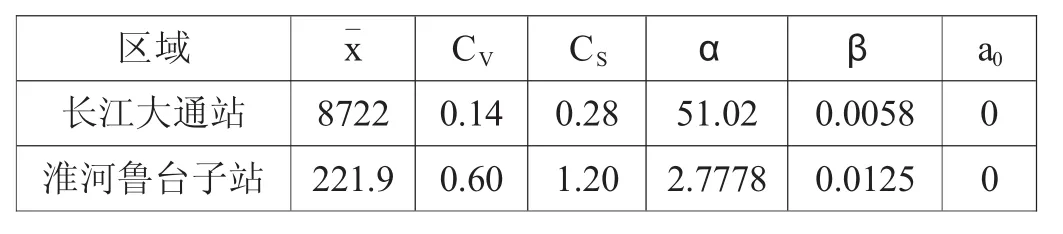
表1 大通站和鲁台子站年径流分布参数估计结果

根据Kolmogorov-Smirnov（K-S）检验法检验大通站和鲁台子站年径流的分布函数是否符合要求，得到统计量D分别为0.09和0.05，小于显著水平位0.05的D值0.21，则接受两者年径流为选定的P-Ⅲ型边际分布。

2.用极大似然估计计算Copula模型的参数

一般地，联合分布函数的密度函数为：

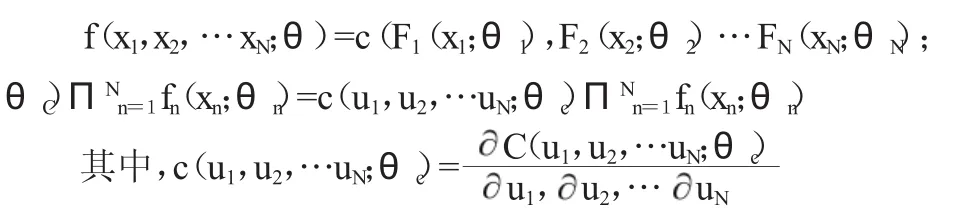
式中：θc为Copula函数的1×mc维参数向量；fn（xn；θn）为边缘分布函数；θn为边缘分布函数Fn（xn；θn）的1× mn维参数向量；θ=（θ1，θ2，…θN；θc）'；n=1，2，…，N。

因此，可以得到使样本（x1t，x2t，…，xNT），t=1，2，…，T的对数似然函数为：

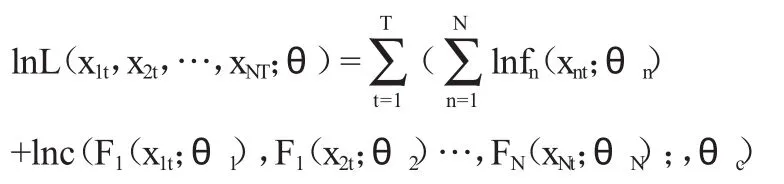
使似然函数取最大值的θ即是最大似然估计值。

而且Copula技术建模的特点是其极适合于采用多阶段估计法，很多学者的实证都表明采用一步极大似然估计法和两阶段极大似然估计法来估计Copula模型，得到的参数估计值差异不显著，所以一般采用两阶段极大似然估计法来估计Copula模型的参数。即首先分别估计出边缘分布的参数θ1，θ2，…θN，然后将其估计值作为已知参数代入Copula函数中，进而估计Copula函数中的参数。两阶段极大似然函数估计使得Copula模型参数的估计问题大为简化。

采用Kolmogorov-Smirnov（K-S）检验来评价联合分布计算频率与联合观测值经验频率的拟合程度，其统计量D计算如下：

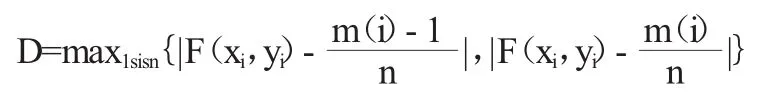
式中：F（xi，yi）为（xi，yi）的联合分布；m（i）为联合观测值样本中满足条件x≤xi且y≤yi的联合观测值的个数。

采用离差平方和最小准则（OLS）来评价Copula方法的有效性，并选取OLS最小的Copula作为联接函数。OLS的计算公式如下：

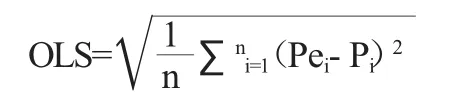
式中：Pei、Pi分别为经验频率和计算频率。

由大通站与鲁台子站年径流的组合分布得出各Copula的参数及评价指标，计算结果如表2。

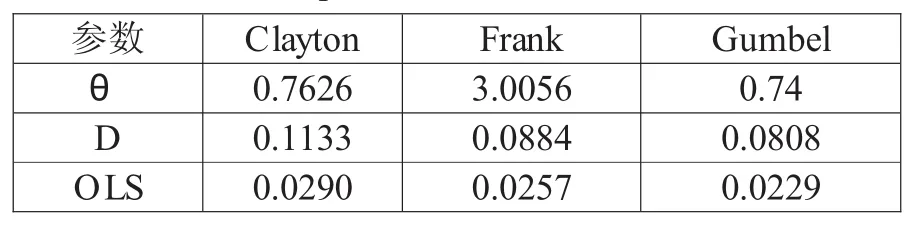
表2 各Copula参数及评价指标计算结果

所选3种函数均能通过K-S检验，因GumbelCopula函数可用于描述具有上文相关特性的相关关系，且OLS最小，因此选用GumbelCopula函数作为联结函数，表达形式为：

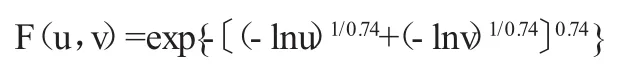
计算分布与经验频率拟合值见图1。

图1 计算分布与经验频率拟合值

四、结果分析

根据以上所建联合分布模型，可以求出长江大通站和淮河鲁台子站年径流遭遇概率，图2给出了长江大通站和淮河鲁台子站年径流的联合分布等值线图。

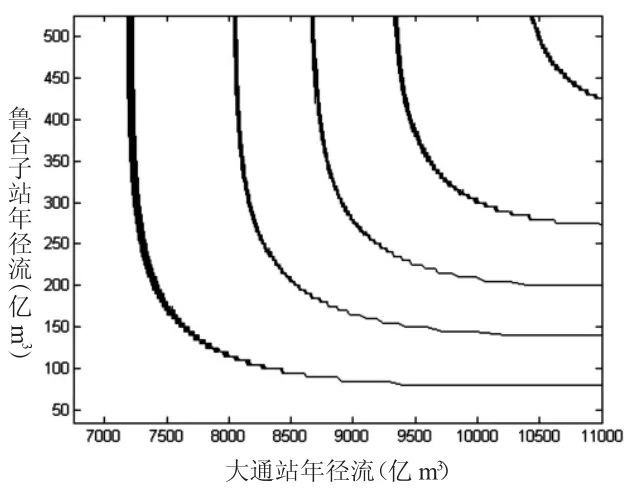
图2 大通站与鲁台子站年径流遭遇

根据上述所建立的联合分布模型对大通站和鲁台子站丰枯频率进行分析。规定其丰枯指标分别为丰水频率pf=62.5%，枯水频率pk=27.5%。分四种情况进行讨论，计算结果见表3。

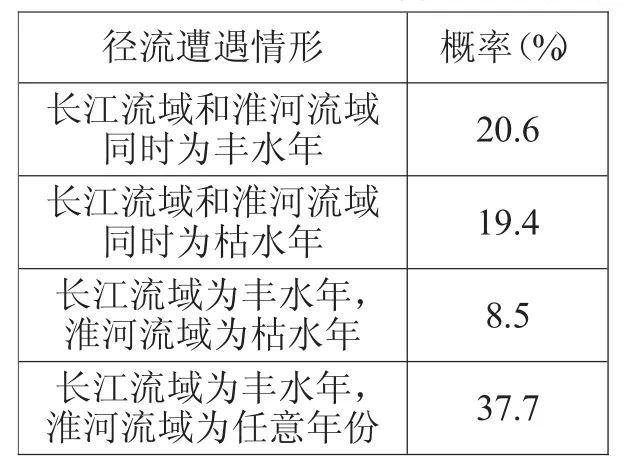
表3 长江流域和淮河流域年径流遭遇分析

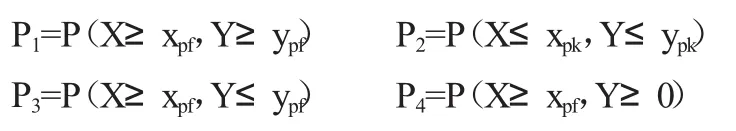
可见，长江流域和淮河流域同为丰水年的概率20.6%；同为枯水年19.4%；长江流域为丰水年，淮河流域为任意年的概率为37.7%；长江流域为丰水年，淮河流域为枯水年的概率为8.5%。因此，长江流域和淮河流域年径流具有丰枯补偿特性，可以相机从长江流域向淮河流域调水■