求解双曲守恒律方程的WENO型熵相容格式*

程晓晗，封建湖，聂玉峰

(1.西北工业大学应用数学系，陕西 西安 710072； 2.长安大学理学院，陕西 西安 710064)

许多物理模型都采用双曲型守恒律方程描述，如气体动力学中的Euler方程、浅水动力学中的浅水波方程和等离子物理学中的磁流体方程等。在一维情况下，有如下形式：

(1)

本文中，进一步研究熵相容格式，通过在单元交界面处进行高阶重构，得到一类高精度的加权基本无振荡(weighted essentially non-oscillatory,WENO)型熵相容格式。最后，通过一些数值算例验证所构造的新格式的性能。

1 WENO型熵相容格式

1.1 一维标量守恒律方程

1.1.1熵守恒格式

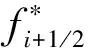
(2)

(3)

与F相容。该格式被称为熵守恒格式，具有二阶精度[2]。

1.1.2熵稳定格式

根据熵稳定条件，在激波等间断位置，总熵应该耗散(减少)。E.Tadmor[2]指出，一个三点格式只需含有比熵守恒格式更多的黏性则是熵稳定的。因此，P.L.Roe[3]提出用Roe格式的数值黏性项作为对熵守恒格式的补充，数值通量为：

(4)

该格式保持了Roe格式对间断的良好捕捉效果，并且无需进行熵修正。

1.1.3熵相容格式

考虑黏性形式的Roe格式数值通量[5]：

(5)

(6)

式中：Δai+1/2=f′ui+1-f′ui，取α=1/6。式(6)定义的数值通量跨过激波时具有足够熵增且数值解保持单调，具有这种性质的通量称为熵相容通量。熵相容格式是目前估计熵的变化最精确的一种熵稳定格式。

1.1.4WENO型熵相容格式

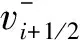
(7)

1.2 一维守恒律方程组

气体动力学中的Euler方程为：

(8)

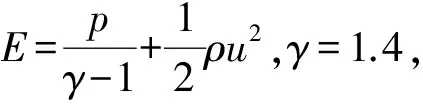
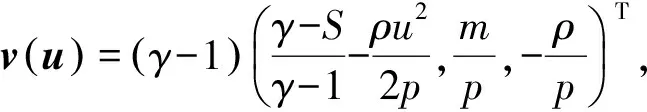
1.2.1熵守恒格式

对于守恒律系统，一般采用逐段分解的构造方法[7]获得熵守恒通量。在该方法中，保持总熵不变的数值通量可以表示为沿熵变量空间内不同路径的积分和的形式。虽然该方法适用于各种守恒律系统，但其计算量过大并且有时候会产生数值不稳定[8]。对于Euler方程和浅水波方程，根据其特定的熵函数，他们的熵守恒通量有比较简单的构造方法。

其中，Euler方程的熵守恒通量的计算方法如下。定义参数变量z为：

(9)

则熵守恒通量为：

(10)

式中：

1.2.2熵稳定格式

与标量守恒律一样，对熵守恒格式添加适当的黏性，可使之满足离散熵不等式。考虑用Roe格式的数值黏性项作为补充，得到关于Euler方程的熵稳定格式，数值通量为：

(11)

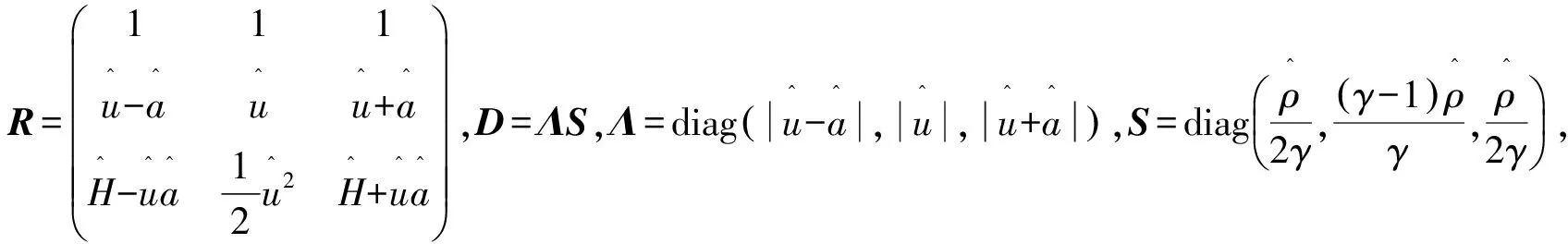
1.2.3熵相容格式

类似标量守恒律，为了抵消解在跨过激波时产生的熵增，需要对D进行修正，令：

D1=Λ+αΔΛS

(12)

式中：ΔΛ=diagui+1-ai+1-ui-ai,ui+1-ui,ui+1+ai+1-ui+ai，于是可以得到Euler方程的熵相容格式，数值通量为：

(13)

1.2.4WENO型熵相容格式

(14)

对于一维守恒律方程组，本文中仅以气体动力学中的Euler方程为例，设计WENO型熵相容格式，其他方程可以参照Euler方程做一些相应的修改，在此不再赘述。

2 数值模拟算例

采用半离散格式：

(15)

时间上的推进一律采用三阶强稳定的Runge-Kutta方法[9]。为了比较，也给出了相应算例的熵相容格式(EC格式)的计算结果。

2.1 线性对流方程连续初值问题

在区域x∈[-1,1]上求解初值问题：

采用周期边界条件，计算到t=10。

本算例可以用来测试格式的收敛性和精度，表1给出了相应的误差L1和L，充分说明了WENO型熵相容格式(EC-WENO格式)的精度能达到五阶。

表1 EC-WENO格式的数值精度Table 1 Numerical accuracy of EC-WENO scheme

2.2 无黏Burgers方程间断初值问题

在区域x∈[-1,1]上求解初值问题：

采用周期边界条件，取CFL系数为0.8，空间网格数为40，计算到t=0.3。

本算例的解主要包括2部分：在左边x=-1/3处由-1到1的跳跃产生了一个稀疏波，在右边x=1/3处由1到-1的跳跃产生了一个定常激波。计算结果如图1所示。由图可知，EC-WENO格式算得的解不仅准确地捕捉到稀疏波，而且在间断位置也没有产生伪振荡，符合“高分辨率”的特性。

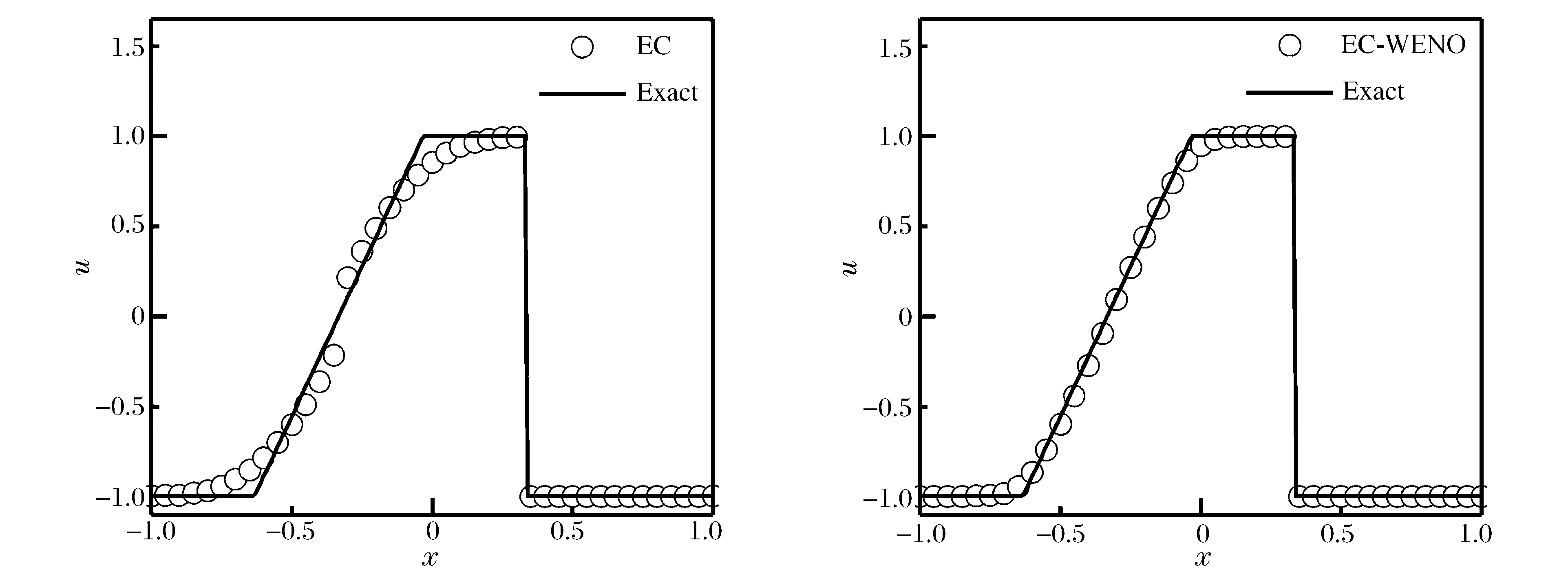
图1 无黏Burgers方程间断初值问题Fig.1 Discontinuous initial value problem of Burgers equation

2.3 一维Euler方程Sod激波管问题

在区域[-0.5,0.5]上求解初值问题：

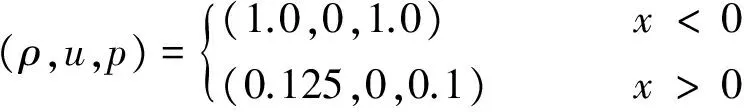
采用Neumann边界条件，取CFL系数为0.4,空间网格数为100，计算到t=0.1。

精确解包括稀疏波、接触间断和激波。密度的计算结果如图2所示。由图可知，EC-WENO格式比EC格式能对解的结构有更准确地捕捉，尤其是对激波的捕捉非常锐利。

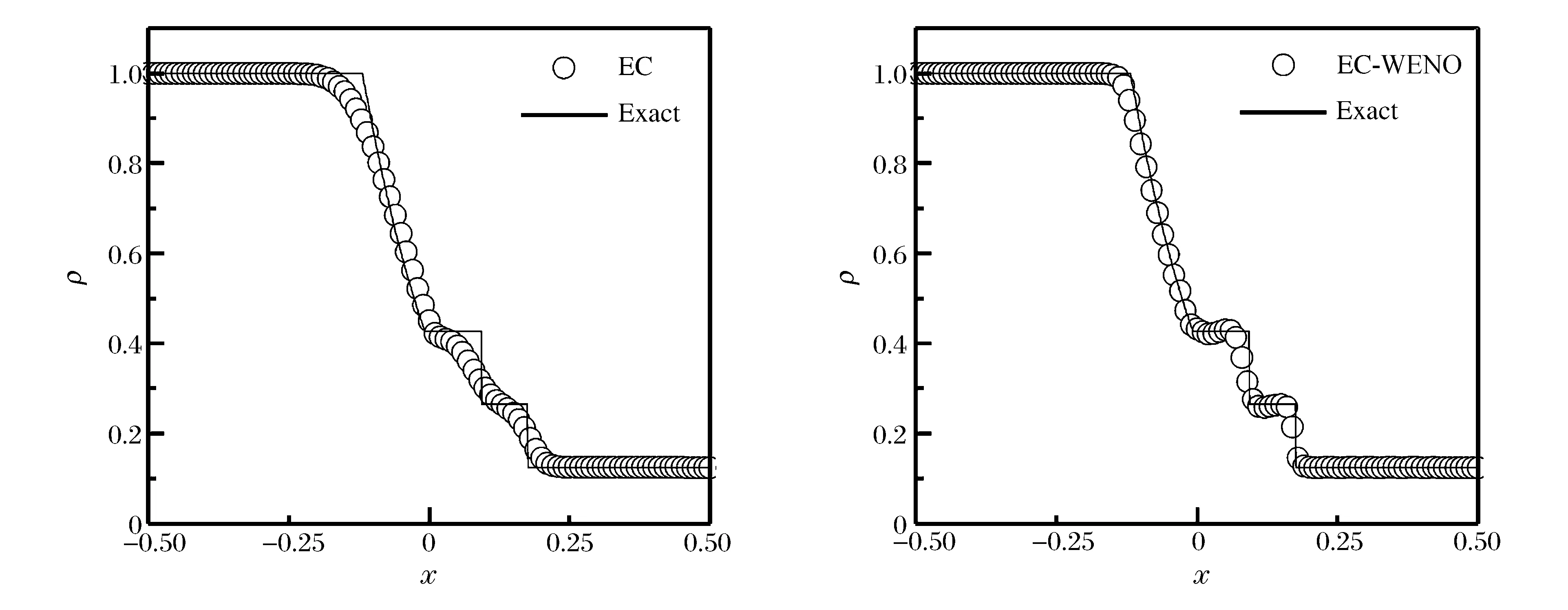
图2 一维Euler方程Sod激波管问题Fig.2 Sod shock tube problem of 1D Euler equation

2.4 一维Euler方程低密度流问题

在区域[-0.5,0.5]上求解初值问题：

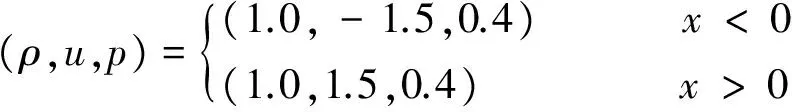
采用Neumann边界条件，取CFL系数为0.4,空间网格数为100，计算到t=0.05。

精确解包括2个强稀疏波和1个平凡的接触间断。由于中间部分的压力非常小，接近于真空状态，很多数值方法容易在该位置出现压力为负的情况(如Roe格式)，导致计算失败。压力的计算结果如图3所示。由图可知，EC-WENO格式能成功地计算低密度流问题，且效果较好，能有效避免非物理现象(如负压力)。

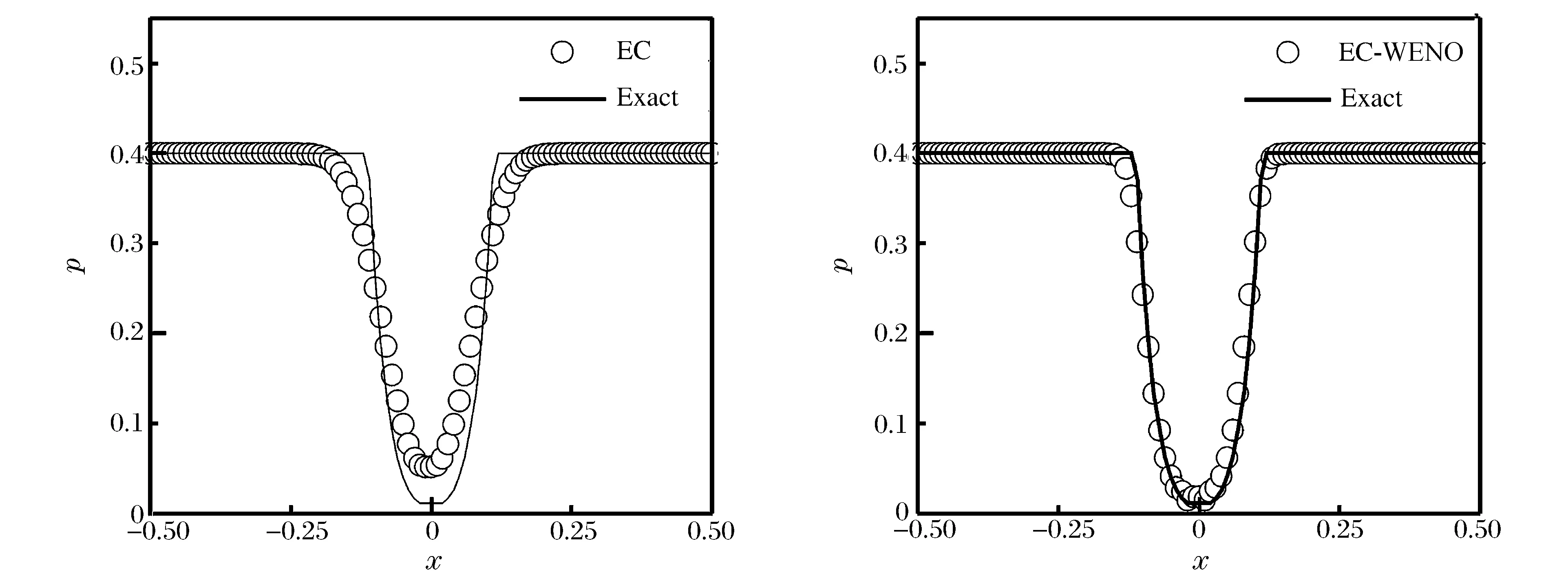
图3 一维Euler方程低密度流问题Fig.3 Low density problem of 1D Euler equation

2.5 一维Euler方程强稀疏波问题

在区域[-10,15]上求解初值问题：

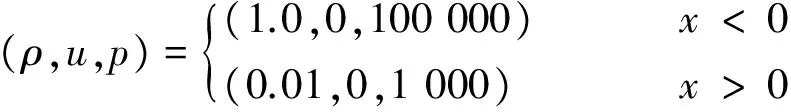
采用Neumann边界条件，取CFL系数为0.4,空间网格数为100，计算到t=0.01。

精确解包括强稀疏波、接触间断和激波。密度的计算结果如图4所示。由图可知，EC-WENO格式取得了非常良好的效果，解在稀疏波有一个平滑的过渡，且在波头波尾位置都非常贴近精确解。

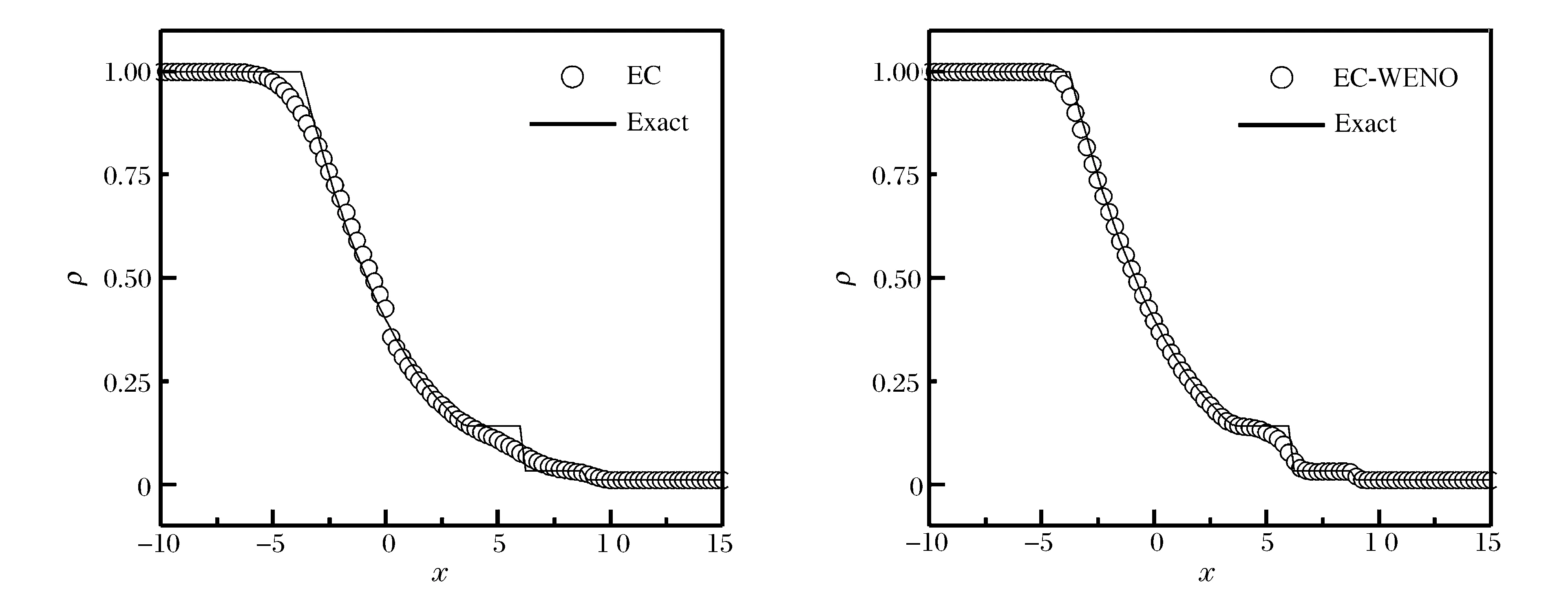
图4 一维Euler方程强稀疏波问题Fig.4 Density of strong expansion problem of 1D Euler equation

3 结 论

以熵相容格式为基础，通过在单元交界面处进行WENO重构，构造了一类求解双曲守恒律方程的WENO型熵相容格式，有效地提高了熵相容格式的精度。数值模拟结果表明，新格式具有高精度、基本无振荡性等特点。

[1] Roe P L. Approximate Rieman solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981,43(2):357-372.

[2] Tadmor E. The numerical viscosity of entropy stable schemes for systems of conservation laws, Ⅰ[J]. Mathematics of Computation, 1987,49(179):91-103.

[3] Roe P L. Affordable, entropy-consistent, flux functions[C]∥Oral Talk at Eleventh International Conference on Hyperbolic Problems: Theory, Numerics, Applications. Lyon, France, 2006.

[4] Ismail F, Roe P L. Affordable, entropy-consistent Euler flux functions, Ⅱ: Entropy production at shocks[J]. Journal of Computational Physics, 2009,228(15):5410-5436.

[5] Tadmor E. Numerical viscosity and the entropy conditions for conservative difference schemes[J]. Mathematics of Computation, 1984,43(168):369-381.

[6] Liu X D, Osher O, Chan T. Weighted essentially non-oscillatory schems[J]. Journal of Computational Physics, 1994,115(1):200-212.

[7] Tadmor E. Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems[J]. Acta Numerica, 2003,12:451-512.

[8] Fjordholm U S, Mishra S, Tadmor E. Energy preserving and energy stable schemes for the shallow water equations[R]. Hong Kong: Foundations of Computational Mathematics, 2008.

[9] Gottlieb S, Shu C W, Tadmor E. High order time discretizations with strong stability properties[J]. SIAM Review, 2001,43(1):89-112.