摆式剪板机剪切过程中的刀片间隙补偿研究

张 进，高建和

（扬州大学 机械工程学院，江苏 扬州 225127）

0 前言

在摆式剪板机剪板过程实验测试中发现，上下刀片刃口间隙量的变化，在整个剪床剪口长度上，中间较两边严重。这也是剪板机在实际工作中造成加工件断口不平整、产生翘曲、断面组织被拉伸扯断的主要原因，不仅影响到剪切质量，而且影响机床受力及刀片寿命[2]。

本文利用Solidworks进行物理模型的建立，然后导入ANSYS Workbench进行了静态有限元分析，分析得到上下刀片的位移变形值，然后利用ANSYS Workbench优化方法优化工作台结构，补偿下刀片变形，进而补偿刀口间隙。

1 摆式剪板机的有限元静态分析

1.1 建立有限元模型

本文对摆式剪板机进行静态分析采用的有限元软件为ANSYS Workbench。ANSYS Workbench用来模拟复杂的多物理场环境的实际工程问题，它在工程项目页面引入了项目流程图，通过各个分析系统间的连接，将分析过程结合在一起，每个分析系统的数值模拟过程一般采用简化假定或者真实的模型，将CAD模型构造成有限元网格模型，再通过施加载荷和边界条件后，运行求解得到分析结果，分析系统之间通过共同变量建立关联[4]。

在本文中，不影响摆式剪板机刚度及强度的情况下，对一些结构进行忽略，如结构中的倒角、圆角及圆孔等。摆式剪板机的有限元模型如图1所示。

图1 摆式剪板机有限元模型

1.2 材料参数

由于只需对剪板机进行静态的刚度分析，所以只需将材料的弹性模量及泊松比等参数赋予相应部件即可，剪板机材料为Q235钢，取弹性模量为210GPa，泊松比 0.3。

1.3 网格划分

网格划分是有限元分析最关键的一个步骤，网格划分的质量和优劣直接影响到解算的精度和速度。它不仅繁琐、费时，而且在许多地方依赖于操作者的经验和技巧。

对本模型一些不规则体进行切割以期划分网格时可以采用扫掠型网格划分方法，得到六面体网格，可以节约计算时间，减少成本。网格划分后的模型如图2所示。

图2 网格划分

1.4 载荷与约束的处理

1.4.1 载荷施加

摆式剪板机剪切力计算大多是依据刀架做直线运动剪板机剪切力算式进行的，即采用前苏联学者诺沙里公式[1]

式中：σb——金属板材的强度极限，MPa；

δx——金属板材的延展率；

h——金属板材的厚度，mm；

k——刀片磨钝系数；

φ——剪切角，°；

X、Y、Z——分别为弯曲系数、剪刃侧向间隙相对值、压料系数。

剪切力计算后，由经验公式算得水平推力及压料力，再由力平衡公式得到两个剪切油缸的作用力大小。计算所得载荷大小如表1所示。

表1 载荷大小

1.4.2 约束的处理

有限元实际计算中必须对约束条件的处理给予足够重视，若处理不当，就不可能获得符合实际的结果，甚至方程出现畸性。本文中机架主要由左右两墙板底面通过地脚螺栓与地面进行固定连接，所以对机架的底面地脚螺栓处施加固定约束；刀架与机架的连接处是钢与钢有润滑的摩擦，取摩擦系数0.05，刀架尾部端面限制Y、Z方向的自由度。

1.5 计算结果分析

剪切力随着剪切位置的变化，剪切力施加位置点也在发生变化，其他的载荷施加点位置不变。所以在本次有限元计算中，剪切力从距刀座左侧100mm处开始施加，共施加8处。

1.5.1 上刀片

从位移云图中可看到，当剪切力施加在刀片中间位置的时候，上刀片沿着X轴负方向变形且中间位置位移变形量较大，影响剪切质量。图3是剪切力施加在距刀座左侧1700mm处的上刀片位移云图。

上刀片位移变形计算结果如表2所示。

1.5.2 下刀片

从下刀片位移云图中可以看到，当剪切力施加在刀片中间位置时，下刀座沿着X轴正方向变形，同上刀架类似，中间位置的位移变形量较大，这样直接导致上下刀刃之间间隙量的变大，影响了剪切质量，严重时会磨损刀片，降低刀片的使用寿命。图4是剪切力施加在距刀座左侧1700mm处的下刀片位移云图。

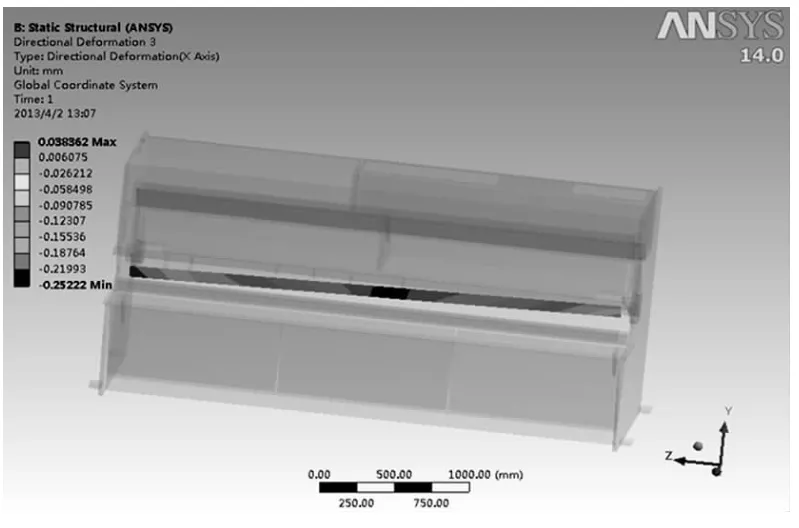
图3 剪切力1700mm加载点位移云图

表2 上刀片计算位移变形量

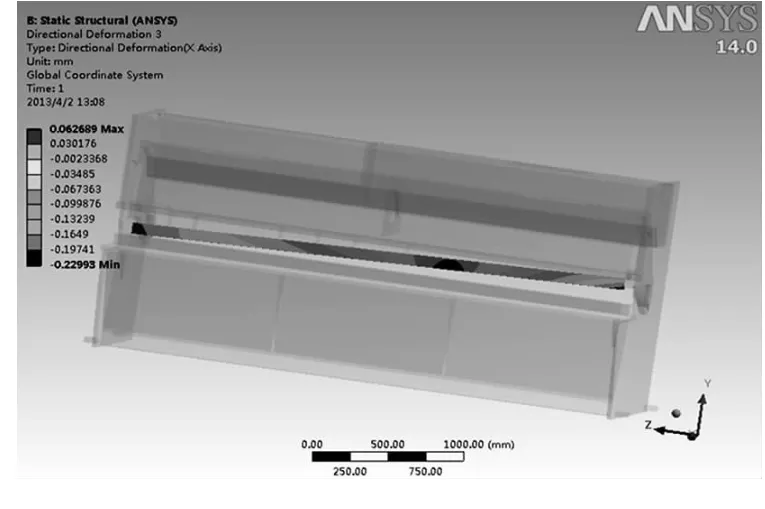
图4 剪切力1700mm加载点位移云图

下刀片位移变形计算结果如表3所示。

表3 下刀片计算位移变形量

为了直观形象地表示出摆式剪板机剪切过程中上下刀片变形量的变化从而导致间隙的变化，将所得数据绘制成曲线，如图5所示。

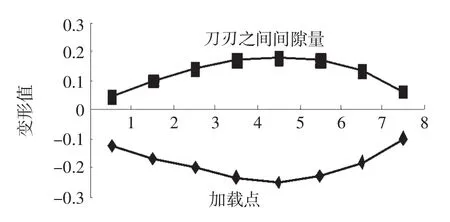
图5 上下刀片变形量

由于本文中的剪板机剪切间隙为0.42mm，剪板机剪切过程中的上下刀片变形量的绝对值加上剪切间隙即为剪板机剪切过程中的间隙量。

2 剪板机间隙补偿

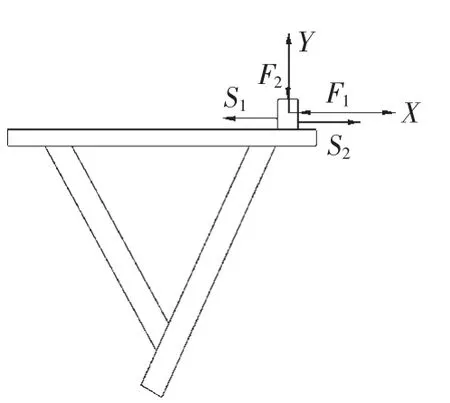
图6 工作台下刀片受力分析

根据摆式剪板机的结构，工作台处的刀片主要承受水平推力F1和剪切力F2，而且工作台易于改造，对间隙的补偿较易实现。如图6所示，在剪切力F2的作用下，下刀片有沿着X正方向变形的趋势，在水平推力F1的作用下，下刀片有沿着X负方向变形的趋势，为使下刀片在F1和F2综合作用下X方向上变形最小，本文采用ANSYS Workbench中的DOE技术（基于Workbench平台的设计变量研究及多目标优化工具，优化设计的主要数据处理工作由DesignXplorer完成）来减小剪板机剪切过程中间隙量的变化，尽量使间隙趋于常值。

以下刀片的位移变形量为优化目标，可以给出最优化问题的数学模型如下式[5]：

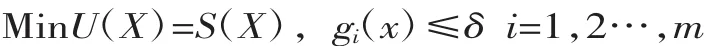
式中，X={α，β，m，n}T称为设计向量或设计变量，S（X）为目标函数，gi（x）为约束条件，这是组成约束函数的基础，而δ则为约束条件的最大值。根据设计要求，约束条件可以是结构的应力或位移，也可以是整个结构的固有频率值。

根据摆式剪板机工作台的结构特点及在工作时的受 力状态，工作台处的两斜板角度及斜板厚度进行优化（图7），得到优化结果如表4所示。

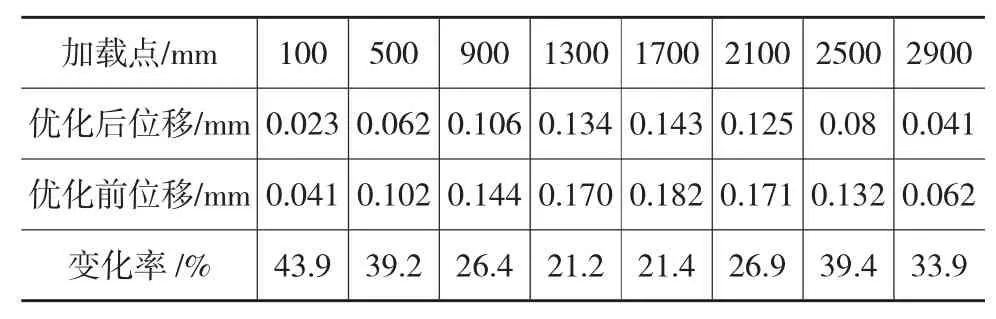
表4 下刀片改进前后结果比较

由优化后的数据得知，下刀片的最大位移变形为0.143mm，而优化前分析计算的最大变形为0.182mm，优化后比优化前的位移变形减小了21%，有效降低了下刀片的变形量，在一定程度上减小了刀刃间隙量。如图8所示更为直观形象地表示出改进的效果。

以图表和响应面的方式显示研究目标随着设计参数的变化情况，主要检验单个或多个参数变化对模型结果产生的综合影响，并分析每个参数及参数之间的相互作用对模型的影响。

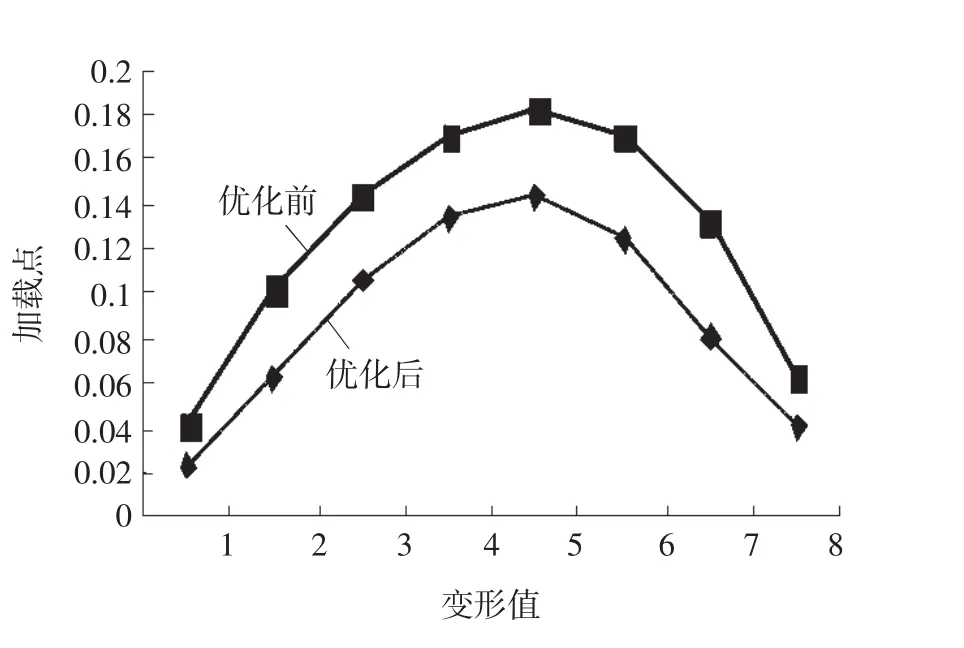
图8 优化前后比较

从图9可以看到单个参数变化的影响，从图10可以看到两角度参数对机床刚度的响应面。

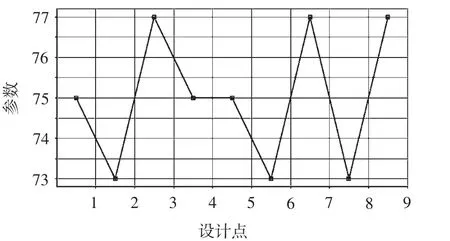
图9 单个角度设计参数的影响

3 结论

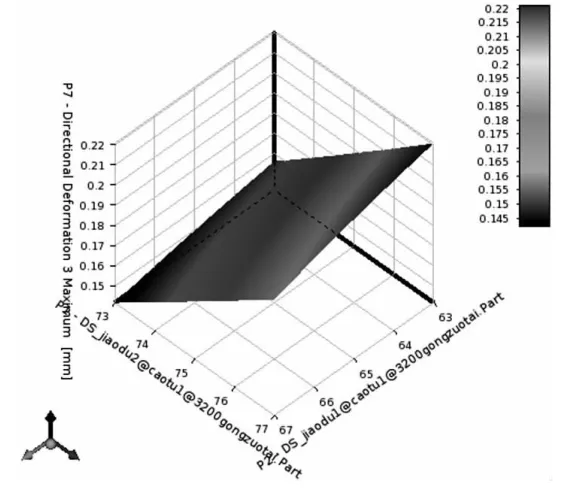
图10 两个角度设计参数的影响

通过对摆式剪板机整机模型的有限元静态分析，得到上刀片、下刀片的位移变形，以及上、下刀刃之间间隙量的变化，利用ANSYS Workbench中的DOE技术补偿下刀片位移变形，减小了上、下刀刃之间的间隙量，提高了剪切质量。

[1] 沈阳锻压机床厂.剪板机设计[M].1978.

[2] 徐会彩，李金山.斜刃剪板机剪切力的研究[J].锻压装备与制造技术，2010，45（4）：29-31.

[3] 张永样.剪板机最佳剪切间隙的研究[J].海军工程学院学报，1995，（1）：49-52.

[4] 许京荆.ANSYS 13.0 Workbench数值模拟技术.北京：中国水利水电出版社，2012.

[5] 马立峰，黄庆学，李 颖，等.新型滚切剪空间剪切机构优化数学模型的建立及应用[J].四川大学学报（工程科学版），2008，（2）.

[6] 周 桓，陈 伶，胡建民.摆式剪板机刀架设计.锻压装备与制造技术，2004，39（1）：20-21.