基于PRO/E的精确三维斜齿轮参数化建模
关欣
辽宁广播电视大学(沈阳 110034)
基于PRO/E的精确三维斜齿轮参数化建模
关欣
辽宁广播电视大学(沈阳 110034)
斜齿轮是参数化建模的热点与难点。当前较为流行的斜齿轮参数化建模方法仍存在曲线的近似替代、齿形生成随意、无精度检测方法等一系列问题。为解决上述问题,从齿条型刀具加工齿轮的范成原理入手,推得齿廓渐开线方程与过渡曲线方程;参数化建模所需基本模型,通过PRO/E的参数化建模功能完成斜齿轮的建模;并提出了一种斜齿轮模型精度的检验方法。
斜齿轮 参数化建模 精度检验
目前,利用PRO/E进行斜齿轮参数化建模已有多种操作方法,存在的问题主要有以下三个方面:(1)参数化模型通用程度不高。由于建模时多采用0.38倍模数的圆弧来代替过渡曲线,忽略了齿根圆与齿轮基圆的位置关系,在特定的齿数下无法生成模型;(2)斜齿轮模型的精确程度不高。部分建模方法采用将直线投影至圆柱面上建立齿轮螺旋线,造成了齿形严重偏离实际加工齿形;另外,螺旋渐开面的生成方式的选择对齿轮模型精度的影响也很大;(3)对生成的齿轮模型精度的检验手段甚少。
1 斜齿轮端面齿廓曲线
1.1 斜齿轮端面齿廓的建立
在PROE中,单击文件→新建,选择零件模型,命名为gear,进入PRO/E建模环境。在gear的开发环境中,单击工具→变量,将表1所示的参数输入其中,单击确定,保存输入参数。
单击工具→关系,在关系对话框中输入斜齿轮的端法面参数关系、直径几何关系以及基圆螺旋角的计算式。注意,这些关系式应采用PRO/E可以识别的显示方程式书写。所输入的关系为:



表1 齿轮的基本参数
生成齿轮的基本圆系。在PRO/E界面中单击草绘按钮,选择FRONT平面,作一组共四个同心圆。单击关系按钮,将四个圆的直径分别设定为分度圆直径、齿顶圆直径、齿根圆直径和基圆直径,如图2所示。

图2 生成齿轮的基本圆系
1.2 生成齿轮的端面齿形
单击按钮,选择从方程,再选取所要生成曲线所在的坐标系,本文以默认坐标系生成曲线。最后选择坐标系类型为笛卡尔坐标系。在弹出的文本框中输入中所得出的渐开线方程与过度曲线方程。注意:渐开线与过渡曲线要分别生成。
建模所用的“渐开线”方程为:

方程中参数的具体含义参见文献[2]。
2 斜齿轮模型的建立
为了构建精确的斜齿轮模型,必须通过螺旋线方程生成螺旋线。目前有些文献中采用的投影直线法是不准确的,A线为由方程生成的螺旋线,B线为投影直线(如图3所示)。
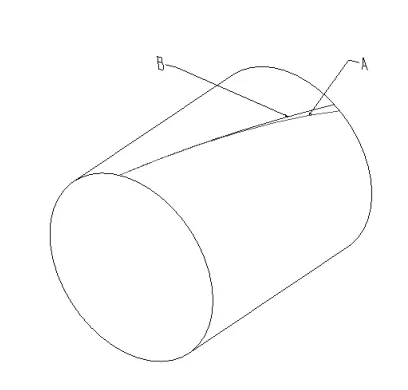
图3 螺旋线
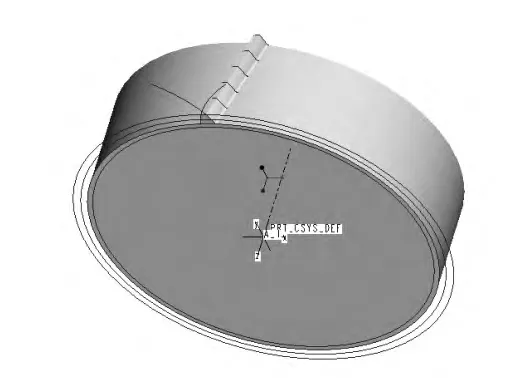
图4 生成的端面齿形
将得到的齿廓曲面进行旋转复制操作。本文采用扫描混合法建立齿轮模型。对于变剖面扫描法的精度问题,将在本文中给出其精确度偏低的实例证明。
扫描混合的成型方法在文献[3]中N大于5时精度很高,故本文采用N=6的该方法进行斜齿轮的造型。对上一步生成的端面齿形进行混合扫描操作。扫描轨迹线既为螺旋线,剖面为生成的端面齿形。如图4。
将生成的第一个轮齿沿轴线阵列,得到斜齿轮模型,如图5。

图5 生成的斜齿轮模型

图6 变剖面扫描方式检验模型
3 斜齿轮模型精度的检验
3.1 变剖面扫描法的检测
变剖面扫描生成斜齿的机理是将端面齿廓沿分度圆上的螺旋线扫描至另一端面,生成齿体。检验所用模型如图6所示。
图6中的圆柱面为与轮坯同心的任意圆柱面。所检验的项目为该圆柱面上的理论齿面螺旋线与该圆柱截齿面所得“螺旋线”上,Z坐标相同的两点的偏差,该偏差用两点间距离表示。
检测任意分度圆柱面上的十个点,得到变剖面扫描法的误差随齿宽方向的变化趋势见表2。
由表2可见,变剖面扫描法得到的齿形误差大约在0.001 mm。
扫面混合法生成轮齿的机理是:先将端面齿廓扭转kβ至另一端面,在两端端面中插入N个端面,将这N个端面沿着螺旋线进行扫面混合,得到齿形。扭转角公式为:
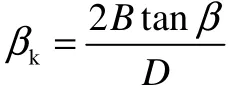

表2 变剖面扫描法精度
采用与检测变剖面扫描齿形形同的方法进行检测。考虑到齿形精度与N值有关,取N=3,N=6两种条件下的齿形进行检验。N=6时,所得数据见表3。
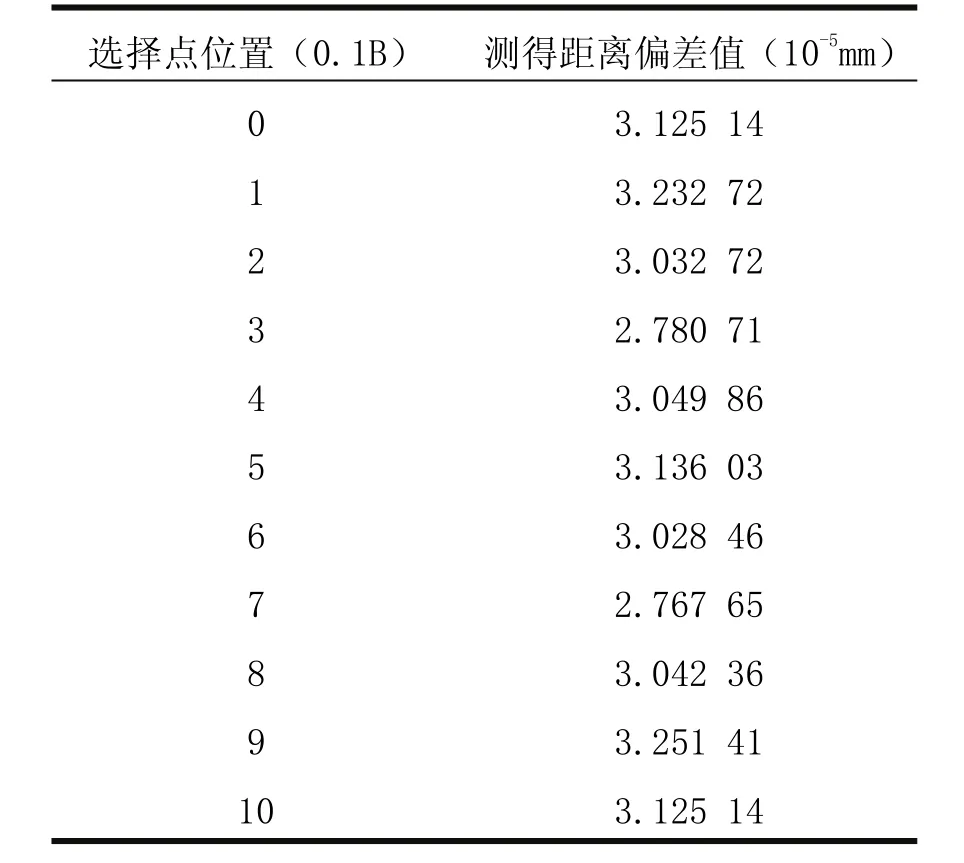
表3 N=6时扫描混合法精度
可见,采用的N=6时的扫描混合法生成斜齿的精度为0.000 03mm左右,远远高于由变剖面扫描法的精度。N=3时,所得数据见表4。
N=3时,扫描混合法的精度明显偏低,除在混合截面附近几点(0、8、10)处精度与N=6相当外,其余各点精度甚至低于变剖面扫描法的精度。
文献[3]中同样得到了上述结论,即扫描混合法生成的斜齿轮模型精度随着N值的增大而提高。本法在N<4时,精度很低,会严重歪曲斜齿轮的实际齿形,在应用中应给予足够的重视。本法在N>10时,精度提高不明显,且会使计算速度大幅下降。权衡利弊,取N=6较为妥当。
采取测量实际齿廓线与理论螺旋线上两对应点间距离的方法来检测模型精度。比测量不同圆柱面上螺旋线的长度[3]得到的数据更具有说服力。

表4 N=3时扫描混合法精度
4 结语
采用齿条型刀具加工齿轮的范成过程推导得到的齿廓的渐开线方程与过渡曲线方程,精确的描述了斜齿轮端面齿形;建立了参数化建模所需要的基本齿轮模型,通过PRO/E自带的参数化建模功能完成了一个斜齿轮的建模过程;提出了斜齿轮齿形的检验方法,可以验证不同方式所生成轮齿的精确性,并可以改进现有方法或验证新的建模方法。生成的斜齿轮模型可以任意改变其独立参数,进而生成所需要的斜齿轮模型。
[1]吴继泽,王统.齿根过渡曲线与齿根应力[M],北京:国防工业出版社,1989.
[2]F.L.Litvin.齿轮几何学与应用理论[M],上海:上海科学技术出版社,2008.
[3]李康,李万莉.Pro/E.构建渐开线斜齿轮方法之精度比较[J],机械设计与制造,2008,(2):80-81。
云龙)

