圆锥形端面电极定长补偿铣削加工建模与实验
郑博文,何 磊,金方进,裴景玉
(上海交通大学机械与动力工程学院,上海200240)
圆锥形端面电极定长补偿铣削加工建模与实验
郑博文,何 磊,金方进,裴景玉
(上海交通大学机械与动力工程学院,上海200240)
电火花铣削能利用简单电极有效地加工复杂三维形状。但由于加工中产生的电极损耗会对所加工型腔的几何精度产生很大的影响,所以必须对其进行有效的补偿。采用定长补偿方法进行电火花铣削加工时,旋转电极的端面会随着加工的进行逐步变成圆锥形且保持稳定,并在无轨迹重叠的铣削加工后产生锯齿状的加工面。为了得到平整的表面,对锯齿面的加工进行了研究,建立了基于圆锥形端面电极的定长补偿算法,通过实验分析了加工到达稳定状态时的波动和误差,实验结果与理论模型相吻合。最后通过加工实例证明了该方法的可行性。
电火花铣削;圆锥形端面;定长补偿;锯齿面;电极损耗补偿模型
电火花铣削技术是用简单形状的电极在数控系统控制下进行分层扫描加工,从而获得所需型腔的加工方法。由于在加工中采用标准电极,省去了成形电极的设计和制造过程,故可简化工艺流程,节省加工成本。由于电火花铣削加工所用棒状电极的截面积要远小于所需加工的面积,电极损耗不可避免,这会直接影响加工精度和效率,所以必须对损耗进行补偿[1]。
针对电火花铣削加工的电极损耗现象,众多学者对此进行了大量的研究[2-7]。虽然针对电极损耗补偿提出了很多方法,但在解决电极损耗方面还存在着一些问题:①缺乏对电极端面损耗形状的描述,从而降低了加工精度;②通过控制分层厚度小于放电间隙,虽能使电极保持初始形状,但由于分层厚度很小,将会导致加工效率极低。
裴景玉等[8-9]提出了微细电火花铣削加工定长补偿方法。由于在加工过程中,旋转电极有径向规划轨迹的进给,同时又有轴向的补偿,电极端面会逐渐变得锐利,在到达稳定工作状态后,电极端面
将会形成一个倒置的圆锥形。这时,可根据加工深度和电极半径等因素计算电极端面的锥角,并已通过实验验证了该计算方法的准确性[10]。本文针对圆锥形电极的铣削加工,建立了基于圆锥形电极的数学模型,并进行了实验验证,最后通过加工实例证明了该方法的可行性。
1 定长补偿加工锯齿面的数学模型
采用定长补偿方法进行连续变向交替加工,以无轨迹重叠方式加工一个矩形面。在XY平面上的加工路径见图1a。实心圆点表示加工起点,空心圆点表示加工终点。电极从起点开始加工,沿着加工路径直到终点,得到的加工横截面见图1b。可看出,加工后留下了明显的锯齿状加工面。针对加工锯齿面,建立基于圆锥形电极的数学模型,从而得到平整的表面。

图1 无轨迹重叠方式加工的矩形面
无轨迹重叠的定长补偿铣削加工结束后,会留下锯齿状的加工面,需对其进行进一步的加工。这里选择沿着锯齿面中每个三角状突起的中间作为轨迹进行定长补偿铣削加工。
图2是加工锯齿面的横截面示意图。选取锯齿面中的一个三角状突起作为研究对象,GEF为上一道加工留下的截面为三角形的待加工部分,GAOB为需去除的部分。经过这一步的加工后,留下的残切AEO和BOF依然是直线,对简化计算及分析处理是有利的。O点为加工面的底部,在加工过程中,底面轮廓会因电极损耗而不断上升,设底面高度的变化曲线为y,底面在上升y的同时,工件的被切削区域即从GAOB变为GA'O'B',最后需根据各个量之间的几何关系,求得残切角度θ和残切高度h。
2 实验和结果
2.1 实验设备和过程

图2 铣削加工锯齿面的横截面
采用四轴联动电火花机床和3R旋转轴组件进行电火花加工实验,并用三维数字测量仪进行测量。为了放大电极损耗的影响,工具电极材料选用黄铜,工件材料选用1Cr18Ni9Ti不锈钢。采用工具电极正极性加工,实验参数见表1。
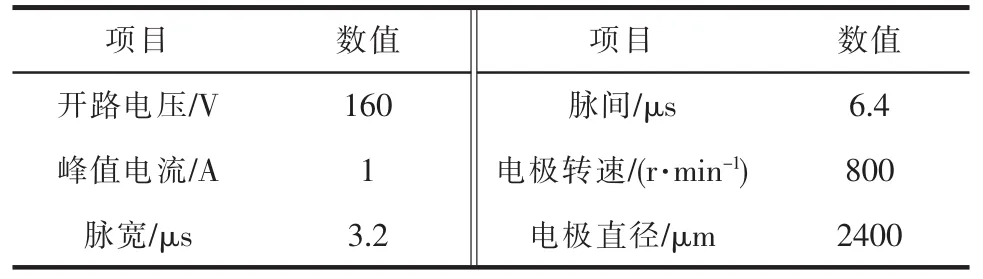
表1 电火花加工参数
采用在工件上加工n个小孔的方法,测得电极的相对体积损耗比和放电间隙[11]分别为65.1%、30 μm,选择的补偿精度le为1 μm,在第一道加工深度即图2所示的HW分别为50、100、150、200 μm的基础上加工三角形截面,加工长度为15 mm。由于文中所用的实验电参数相同,故其电极损耗率保持不变。
2.2 电极端面形状的形成过程
电火花加工过程中,电极的形状直接“拷贝”式地反映在工件的加工槽中。在定长补偿下,使用圆柱电极进行某一深度的层铣削时,电极在这个行程下的损耗情况就实时地表现在工件的加工槽中。故可通过观察工件加工槽连续变化的形状来了解电极在各个行程下的端面形状。由于对锯齿面的定长补偿加工是在上一道加工结束后直接进行的,对电极端面并没有处理,所以电极的初始端面是圆锥形的。定长补偿方法自身的特性使电极尖角变化也是一个逐渐的过渡过程。将加工槽用线切割每隔1 mm切开,分别观察加工过程中前6 mm的加工截面。图3是铣削加工锯齿面从初始到形成稳定电极端面过程的横截面示意图,可看出,变化过程是角度逐渐钝化的一个过程。
2.3 残切底角θ与分层厚度的关系
为便于表述,用θ50表示第一道分层加工深度即HW为50 μm时获得的θ角度值,θ100、θ150、θ200同理。获得数据的方式是通过先测量对应图2所示的∠AOB,该值与180°间的差值再除以2获取的。

图3 铣削加工锯齿面过渡过程的横截面示意图
图4是在不同的定长补偿分层加工深度HW下,加工锯齿面后的θ角大小。在经过5 μm左右后,θ角度值进入一个稳定状态。在稳定状态下,θ角度值呈现出一定的波动性,但波动很小,θ100与θ200的波动最大为0.3°,θ150次之为0.2°,θ50波动最小为0.1°。实际上也只有角度值在极小范围内变化才有意义。角度变化在底面轮廓波动变化上会有一个放大效应,底面轮廓的起伏变化增大,必然造成加工底面精度的降低,从而破坏加工效果。
表2是实验θ值与理论θ值的对比。由于加工长度5 mm前的一段为过渡过程,故取实验θ值为加工长度6 mm后所测值的平均值。可看出,实验值与理论值间的误差较小。
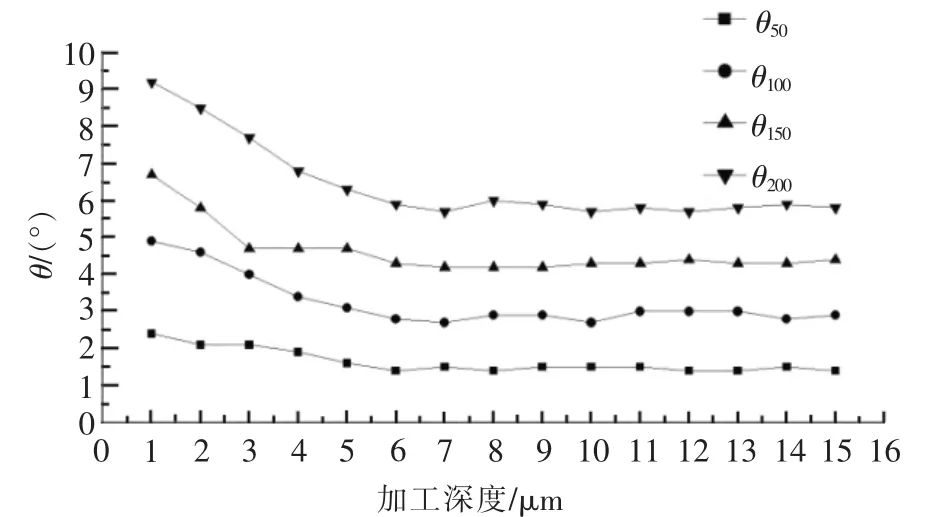
图4 不同分层加工深度下的θ值
2.4 残切高度h与分层厚度的关系
依据残切底角θ分析,前5 mm的角度尚未到达稳定态,则有理由认为深度值也可能尚未稳定,故同样取5 mm后的值来取平均值计算。由于同样存在尖端损耗,故依然引入实际实验值h1(实际残切高度)和理想实验值h2(理想残切高度),h1为加工后直接测量的残切高度值,h2为在h1基础上角度延伸后的高度值。h为通过计算得到的残切高度值。实际实验值h1和理想实验值h2的误差见图5。

图5 残切高度h1和h2示意图
由表3可知,理想实验值h2和理论值h之间的误差,在分层加工深度200 μm时最大为5.1 μm,其他3个分层加工深度下都为3 μm左右;而相对误差在分层加工深度50 μm时最大为15.6%,其他3个分层加工深度下的误差较接近。理想残切高度h2与理论值h之间存在一定的误差,其原因在于第二道加工后,加工轨迹两侧仍会留有残切,理论上残切会有尖锐的突起,而尖端电荷集中会使该突起处也存在尖端损耗的现象,使突起点被钝化,造成误差的扩大。
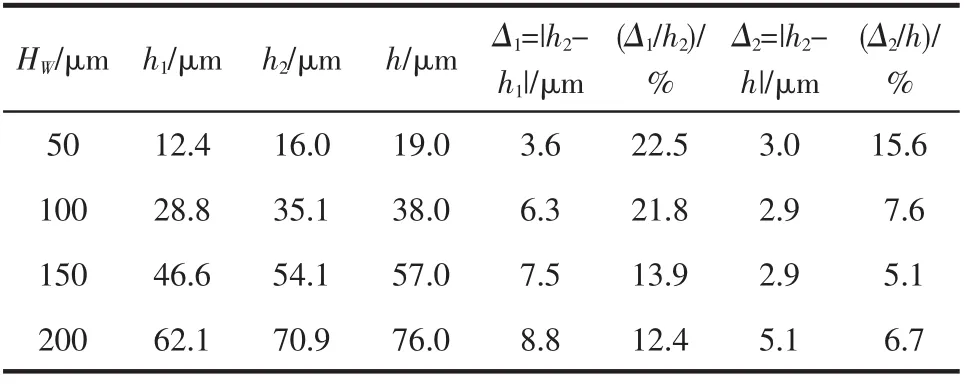
表3 不同分层加工深度下h的误差
2.5 加工实例
取分层加工深度为50 μm,加工两层的方形型腔。每一层的加工分为三步,每一步的加工轨迹见图6。根据以上分析,加工完两步以后,还会存在彼此平行的一条条横截面形似三角形的凸出残切。最后利用等损耗补偿方法去除前两步留下来的残切,加工方向选择与前两道加工方向垂直。型腔边长为7.21 mm,4个顶角半径为1.2 mm。
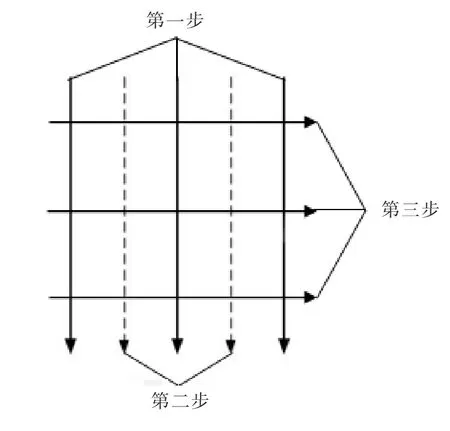
图6 加工方型腔的加工路径
图7a是加工方形型腔的显微照片。使用直径100 μm的微细电极作为探测头,利用机床的接触感知功能测量所加工型腔的深度。图7b是该型腔的底面轮廓。经测量,底面平均深度为104 μm,深度的最大值与最小值相差8 μm,表面粗糙度为Ra0.3 μm。
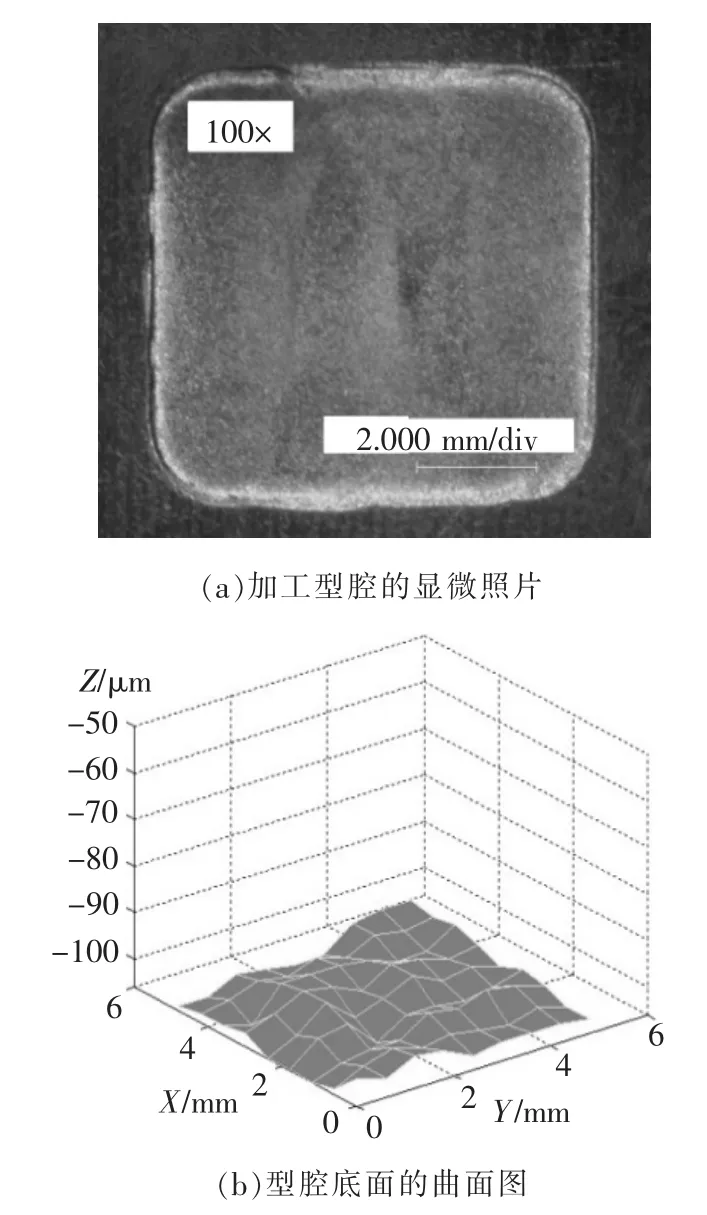
图7 加工型腔的显微照片
3 结论
针对圆锥形电极加工锯齿面,建立了能有效加工锯齿面的数学模型,并进行了实验分析,得到以下结论:
(1)通过对加工端面的观察,发现在加工5 mm左右后趋于稳定。研究了电极端面在形成稳定加工前的过渡过程,发现电极端面变化是角度逐渐钝化的过程。
(2)由于加工锯齿面时,加工截面为三角形,所以相对于加工平面时,电极就形成了锥度较缓的圆锥形端面,并分析了形成这种形状的原因。
(3)通过实验对残切底角θ和残切高度h进行了验证与分析,发现两者能保持稳定,且所得的实验结果与理论计算能很好地吻合。
(4)用圆锥形电极加工两层方形型腔,证明了该方法的可行性,能得到较好的加工效果。
[1] 杨洋,王振龙,赵万生.微细电火花铣削CAD/CAM方法研究[J].机械工程学报,2003,39(9):97-100.
[2] Yu Z Y,Masuzawa T,Fujinoa M.Micro-EDM for threedimensional cavities[J].Annals of the CIRP,1998,47(1):169-172.
[3] Rajurkar K P,Yu Z Y.3D micro-EDM using CAD/CAM [J].Annals of the CIRP,2000,49(1):127-130.
[4] 李剑忠,栾继杰,虞慧岚,等.微细电火花三维加工中电极损耗补偿新方法 [J].大连理工大学学报,2011,51 (4):525-528.
[5] 肖鹿.基于网格划分的微细电火花电极损耗补偿方法[D].大连:大连理工大学,2012.
[6] Dong Y H,Zhao Y C,Wang Z L.Micro-EDM milling of complex 3D structurewith fix-length compensation method[J].Journal of Wuhan University of Technology,2009(7):241-243.
[7] 迟关心,褚旭阳,狄士春,等.管电极微细电火花铣削加工[J].吉林大学学报,2011,41(1):121-126.
[8] 裴景玉,邓容,胡德金.微细电火花加工的底面轮廓模型及定长补偿方法 [J].上海交通大学学报,2009,43 (1):42-46.
[9] 许加利,李建功,裴景玉,等.单层多道微细电火花定长补偿加工方法[J].电加工与模具,2009(3):15-18.
[10]金方进,裴景玉.基于圆锥形端面电极的电火花铣削加工定长补偿方法研究[J].电加工与模具,2012(2):21-24.
[11]邓容,吴品,裴景玉,等.微细电火花加工损耗补偿的研究[J].电加工与模具,2007(4):20-23.
Arithmetic and Experimental Study of Fix-length Compensation Based on Conical Bottom Shape of Electrode in EDM Milling
Zheng Bowen,He Lei,Jin Fangjin,Pei Jingyu
(Shanghai Jiao Tong University,Shanghai 200240,China)
Electrical discharge milling with a simple-shaped electrode is an effective machining method to fabricate complex three-dimensional structures.However,the serious electrode wear occurring in the machining process significantly deteriorates the geometrical accuracy of the products,so effective compensation method need to be conducted.Bottom shape of electrode will become conical under fix-length compensation method combined rotating tool electrode.After EDM milling in non-path overlapped manner,there is serrated surface remained.So this paper proposes the fix-length compensation method with conical bottom electrode,then do experiment and analyze fluctuation and error of the results respectively,the experimental results are very consistent with theoretical results.A demonstration cavity ismachined with thiscompensation method.The effectivenessofthis compensation method is verified.
electrical discharge milling;conical bottom shape;fix-length compensation;serrated surface;mathematical model of electrode wear compensation
TG661
A
1009-279X(2014)01-0009-04
2013-09-06
国家自然科学基金资助项目(51205252)第一作者简介:郑博文,男,1989生,硕士研究生。

