高通滤波在损伤检测中的应用

张炜，曾义权

（中国人民解放军91379部队，山东青岛 266002）

结构的健康监测（SHM）在维护结构的完整性和安全性，避免灾难性事故等方面具有重要意义。在众多的结构健康监测技术中，以振动响应为基础的损伤检测方法，由于其实现简单，受到了广泛的关注。损伤会造成结构物理特性的改变，如刚度的降低会造成结构固有频率的降低，因而利用结构固有频率的变化可以检测损伤的存在。但是由于固有频率属于结构的全局量，只能用于损伤的识别而不能用于损伤的定位[1]。

为了确定损伤的位置和大小，科研工作者进行了大量的研究[1]。大多数的算法需要提供结构完整状态下的数据，这往往难以做到。利用曲率模态的方法可以有效识结构的多处损伤[2]，但是这种方法要求提供结构损伤前的曲率模态。为了解决这一问题，学者们进行了许多的研究和探索，其中空间小波变换进行梁结构的损伤识别方法已被广泛采用[3]。对位移模态进行小波变换，在损伤处会出现小波系数模的极大值，以此来实现对损伤的定位，而良好检测结果的获得，需要选择合适的母小波和变换尺度，而且研究结果表明，仅仅利用小波系数很难识别损伤程度[4]。为此，Douka[5]提出了可以反映损伤程度的强度因子，但强度因子的求得却带来了巨大的计算量。康兴无[6]等从结构刚度和柔度矩阵的正交性出发，结合有限元理论和矩阵摄动理论，提出基于柔度变化的结构损伤检测指标，并通过平面桁架结构的数值模拟证明了该方法的有效性。

提出了基于高通滤波的结构损伤检测方法，该方法具有不需要结构完整状态下模态信息的优点，而且计算快捷，损伤定位准确，同时可以为损伤程度的估计提供重要参考依据。文中先以双裂纹梁为例给出了含裂纹梁的模态分析，然后阐明了基于高通滤波的损伤检测的原理，并给出了数值算例，讨论了仿真处理的结果，最后分别以单裂纹梁和双裂纹梁为例，进行了实验验证。

1 含裂纹梁的模态分析

一悬臂梁长L，宽和高都为h，如图1，裂纹模拟为无质量扭转弹簧，裂纹位置为l1和l2，裂纹深度分别为a1和a2。

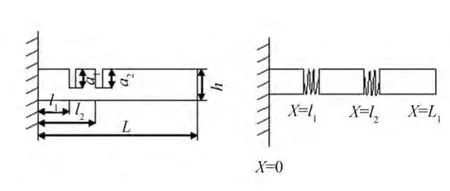
图1 双裂纹悬臂梁模型

由文献[7]可知，裂纹处的局部柔度可表示为

其中a为裂纹深度，E为悬臂梁的弹性模量，I为转动惯量，J(a h)为柔度函数，其表达式如下

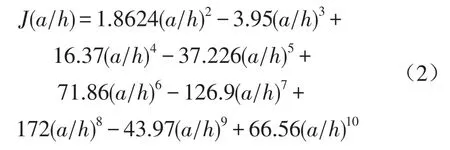
每段梁的位移为

上式中K4=ω2ρAl4(EI),其中A为梁的横截面积，ω为梁的振动角频率，ρ为梁的密度，ti(i=1～12)为未知系数。悬臂梁边界条件如下

裂纹处的连续性条件为

由式（4）、（5）、（6）可得12个方程，写成矩阵形式

由(7)式有非零解可得特征方程

解特征方程可得到梁的任意阶固有频率K，再K代回（7）式，可得到系数ti(i=1～12)，将K和ti(i=1～12)代回（3）式得到模态振型。

2 基于高通滤波的损伤检测

图2（a）表示实验测量所得的损伤梁的结构模态，可以把它看成由两部分组成：没有损伤和噪声的完整梁模态（图2（b））和由损伤和噪声组成的不规则成分（图2（c））。一般情况，在损伤很小的时候，模态变化不明显，无法从模态上区别出损伤点，为了克服这一情况，可以直接利用高通滤波的方法过滤掉模态中无损伤的模态，仅仅提取出损伤的成份来观察，这样就能把细小的损伤信号放大，使之一目了然。假设测量模态为M，完整模态为W，损伤和噪声为R，则有

滤波是有选择的提取或去除信号中某些频率信号，高通滤波就是衰减或滤除掉信号的中的低频率分量，保留信号中的高频分量，强化信号的锐变[8]。若M(x)为测量模态，H(x)为滤波函数，则有

输出R(x)为输入M(x)与滤波函数H(x)的卷积。

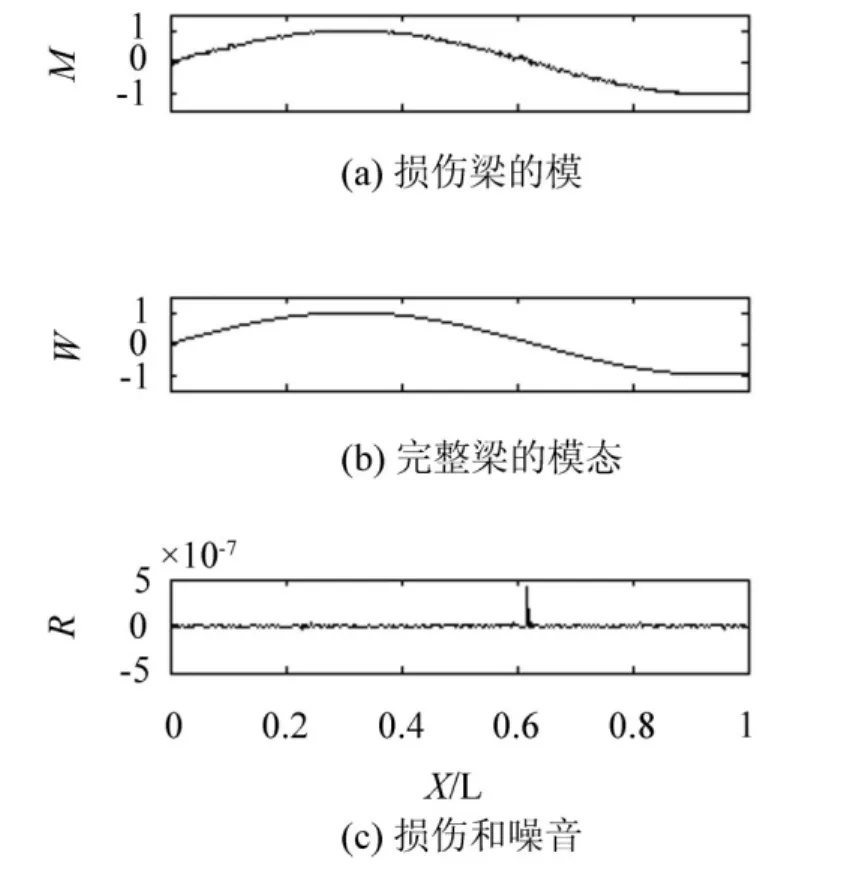
图2 测量模态的组成

3 数值算例

以双裂纹的悬臂梁为例，对所述的高通滤波方法进行数值模拟。一悬臂梁长300 mm，宽度b和高度h均为10 mm，假设梁的固定端在x=0处，第一条裂纹的位置为l1=30 mm处，相对深度为0.05，第二条裂纹的位置l2=150 mm，相对深度为0.05，计算模态时，悬臂梁每隔1 mm一个点共301个点，运用前文所述的模态分析方法可得前四阶模态振型如图3所示。

图3 悬臂梁前四阶模态振型

显然，从图3无法直接得到裂纹位置。

3.1 损伤的定位

运用巴特沃斯数字滤波器对前两阶模态进行高通滤波，巴特沃斯滤波器最早由英国工程师斯替芬•巴特沃斯提出，其特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。巴特特沃斯数字滤波器可以直接通过Matalb软件中的butter函数实现，其调用格式为[b，a]=butter(n，Wn，’high’)，n表示滤波器阶数，Wn表示截止频率，为归一化频率，high表示高通滤波。利用巴特沃斯2阶和4阶高通滤波，截止频率为0.08，取滤波后值R的平方，分析结果图7。

从图4可以清晰的看到，前两阶模态中在损伤置会出现尖锐的突变,对损伤位置的识别效果非常好，同时可以看出，对于相同损伤程度的不同位置，在同阶模态中有不同的突变值，对于同一位置的相同损伤程度，在不同阶模态中也有不同的突变值。但在同阶模态中的相同位置，不同损伤大小呈现出有规律的突变，这点可以作为估计损伤程度的依据。同时，从图4可以看到，选择适合的滤波器参数，会得到更好的结果。

图4 模态振型的巴特沃斯高通滤波

3.2 损伤程度的估计

下面仍以上述规格悬臂梁为例，假设其只在150 mm处有一条裂纹，分别取0.10h，0.15h，0.20h三个不同的损伤深度，研究其对滤波后结果的影响。以1阶模态为例，图5表示损伤标准R2和随损伤深度之间的变化关系（为了看得更清楚，将损伤因子纵坐标取对数），可见，R2的值随损伤深度的增加而增大。因此，对于同一损伤位置，可以将突变值的大小作为评估损伤程度的依据。

4 实验分析

该实验用一铝质梁，长度L=510 mm，宽b=30 mm，高h=5 mm。实验一裂纹位于255 mm处，实验二中裂纹位于150 mm和300 mm处，裂纹深度均为2 mm。将梁平均分成17段，每段长度为30 mm。实验设备为江苏联能电子技术有限公司的振动力学综合实验系统，如图6所示。

图5 R2随损伤深度的变化

图6 振动力学综合实验系统

利用冲击激励法测量损伤梁的模态参数，采用逐点激励，单点响应的方式，响应测量点选在第五点，实验的采样频率为5 000 Hz，用力锤依次对17个点进行敲击，每个点敲击3次得到传递函数的平均值，最后由配套软件得到损伤梁的结构模态。观察实验结果发现该实验的2阶模态具有较小的阻尼比，实验测得2阶模态如图7所示。

图7 实验测量2阶模态

图8为实验测量2阶模态的高通滤波分析结果。

实验一的检测结果与实际损伤位置略有偏差，这是由于实验误差所造成的。实验二的高通滤波结果与裂纹位置完全一致。

图8 单双裂纹梁2阶模态高通滤波

5 结语

从理论和实验两方面验证应用高通滤波方法检测结构损伤的有效性，这种方法直接从实验测得的模态入手，不仅不需要结构健康状态下的模态信息，而且可以快速准确的识别结构的一处或者多处损伤，滤波后的损伤标准R2可以很好的反映出损伤的程度，依此可以对损伤程度进行定量分析，但对于损伤程度的精确计算，还需要进一步深入研究，同时需要提高测试设备的精度，以获取更精确的测量数据，使分析结果更接于实际损伤的情况。

[1]王术新，姜哲.基于结构振动损伤识别技术的研究现状及进展[J].振动与冲击，2004，23(4)：99-102.

[2]刘义伦，时圣鹏，廖伟.利用曲率模态识别桥梁损伤的研究[J].振动与冲击，2011，30(8)：77-81.

[3]Wang Q and Deng X.Damage detection with spatial wavelets[J].International Journal of Solids and Structures,1999,36,927-939.

[4]Quek S,Wang Q,Zhang L and Ang K.Sensitivity analysis of crack detection in beams by wavelet technique[J].International Journal of Mechanical Science,2001,Vol.43,2899-2910.

[5]Douka E,Loutridis S and Trochidis A.Crack identification in beams using wavelet analysis[J].International Journal of Solids and Structures,2003,Vol.40,3557-3569.

[6]康兴无，陈世健，刘勇，马慧娟.一种基于柔度的结构损伤定位新方法[J].噪声与振动控制，2009，6：40-43.

[7]Shifrin EI.Ruotolo R.Naturalfrequenciesofa beam with an arbitrary numberofcracks[J].Journal of Sound and Vibration,1999(03):409-423.

[8]雷学堂，徐火希.FIR数字高通滤波的时域和频域物理分析[J].吉首大学学报(自然科学版)，2006，27(5)：66-71.