LWS400卧螺离心机参数变化对转鼓强度和刚度的影响

李 龙

（天华化工机械及自动化研究设计院有限公司， 甘肃 兰州 730060）

LWS400卧螺离心机参数变化对转鼓强度和刚度的影响

李 龙

（天华化工机械及自动化研究设计院有限公司， 甘肃 兰州 730060）

采用Solid Works软件建立LWS400卧螺离心机转鼓几何模型并导入ANSYS Workbench软件中进行有限元分析。分别改变转鼓转速、转鼓壁厚和液池深度三个参数并讨论由此对转鼓强度和刚度的影响，以便为后续的优化设计方案提供参考。讨论结果表明：转鼓转速的提高或壁厚的减小都对转鼓强度和刚度有明显的影响，液池深度的变化对转鼓强度和刚度的影响不大。

卧槽离心机；转鼓；有限元分析

目前，离心机转鼓的强度设计按照文献[1]进行。LWS400卧螺离心机转鼓是由大、小端盖、两段圆柱形通体和一段圆锥形筒体组成，各部分用止口螺钉拼接。LWS400卧螺离心机用于工业油性污泥的液—液—固三相分离，在处理这种难分离的物料时，应采用大长径比、高转速的卧螺离心机进行分离操作。根据文献[1]，当转鼓长径比大于4.5会增加转鼓的加工难度，工业上一般不采用；LWS400卧螺离心机转鼓筒体由三节筒体拼接而成解决了大长径比卧螺离心机转鼓整体加工制造困难的问题。根据文献[2]设计制造的转鼓尺寸往往具有较大的安全余量，这样会造成材料不必要的浪费；文献[3-5]对卧螺离心机参数和转鼓强度的关系进行了研究分析，但这些文献所研究的对象均为整体制造的转鼓，至于分段拼接的转鼓是否适用于以上文献所得的结论则没有说明。因此，结合LWS400卧螺离心机转鼓自身结构的特点，讨论参数变化对其强度的影响，可以为转鼓后续的尺寸优化提供参考，有一定的工程意义。

LWS400卧螺离心机，转鼓内径Di=400 mm；壁厚t=15 mm；圆柱段转鼓长度L1=1 135 mm；圆锥段转鼓长度L2=600 mm；转鼓总长L=1 800 mm；圆锥形转鼓锥度1∶3.5；转鼓材料密度ρ1=7.85 g/cm3；油性污泥密度ρ2=1.021 1 g/cm3。

1 转鼓有限元模型的建立

用转鼓总体最大应力强度来表征转鼓的应力状态，用材料的许用应力Sm来衡量。转鼓用材304（即0Cr19Ni9）不锈钢，其许用应力Sm为：

其中：σs—设计温度下转鼓材料的屈服极限，205 MPa；

σb—设计温度下转鼓材料的强度极限，520 MPa；

ns—屈服极限下的安全系数，一般取2～2.5；

nb—强度极限下的安全系数，一般取3.5～4。

由式（1）得Sm=102.5 MPa。对于转鼓的总体最大应力强度，需要考虑结构不连续部分的弯曲应力，因此取许用应力的1.5倍作为设计许用应力即153.75 MPa。

转鼓的刚度限制原则需要保证转鼓运行时不能与机壳发生碰撞摩擦。根据设备安装尺寸，LWS400卧螺离心机转鼓的刚度条件为：径向变形不超过6.5 mm；轴向变形控制在3 mm内。

1.1 模型简化及网格划分

为了控制计算规模，将大、小端盖上一些不影响刚度的结构去除；将筒体、端盖之间的螺钉连接和相应的螺纹孔去除；将筒体内壁与筋条的焊接部分作为整体结构处理。

进行网格划分时，使用软件默认的solid187划分模型。在划分过程中对于四面体单元应使用保留中间节点的设置，网格划分后的结果为 1 434 752个节点，730 054个单元。

1.2 载荷和约束的施加

正常工况下，卧螺离心机转鼓受自身质量产生的离心力和被分离物料对其内壁产生的压力作用。在有限元分析中，对转鼓施加如下载荷：

（1）转鼓自身质量产生的离心力

该载荷以角速度形式施加在整个模型上，计算公式为：

ω=2πn/60=303.69 rad/s （2）

其中：n—转鼓转速，2 900 r·min-1。

（2）被分离物料对鼓壁产生的压力

转鼓内的物料由于离心力场的作用会对筒体内壁产生压力作用。有限元分析中，对该载荷以均布载荷的形式施加到转鼓内壁作用面上，方向沿转鼓内壁的法线方向。圆柱形转鼓内壁所受到的物料离心压力为：

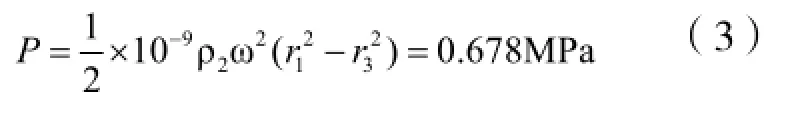
其中：r1—转鼓内半径，200 mm；

r3—自由液面半径，160 mm。

对于圆锥形筒体内壁和大端端盖开有工艺孔（模型中已省略）的端面内壁上任意半径处的离心液压也按照上述方法予以定义。

约束的施加需要根据实际工况选择，可以是某种特定的约束，也可以是几种约束的组合[6]。LWS400卧螺离心机转鼓大小端均由轴承支撑，分别在转鼓大、小端盖与轴承的接触面上施加圆柱约束来限制转鼓的轴向、径向方向的位移。

2 参数变化对转鼓强度和刚度的影响

LWS400卧螺离心机正常工作时转鼓转速为2 900 r·min-1，液池深度40 mm。在各工况下，分别改变转鼓转速、转鼓壁厚和液池深度三个参数对转鼓进行静力分析来讨论强度和刚度的变化。

2.1 转鼓转速变化对转鼓强度和刚度的影响

转鼓内径一定时，转鼓转速越大，分离效果越好。但转鼓转速的增加受到转鼓材料机械强度的限制。将转鼓转速2 900 r·min-1以200 r·min-1为单位分别增大和减小来分析转速变化对转鼓强度和变形的影响。表1和图1分别为最大应力强度随转鼓转速变化的数据结果和变化曲线。根据表1和图1可知：不同工况下，转鼓应力强度均随着转鼓转速的增加而增大。在转鼓材料及其他结构参数一定的情况下，正常工况下当转鼓转速达到3 100 r·min-1时，转鼓应力强度最大值已经非常接近于 1.5Sm，即在现行尺寸参数下，LWS400卧螺离心机所允许的最大转速为3 100 r·min-1。如果想通过增大转鼓转速进一步提高分离因数，可以考虑选择更高强度的转鼓材料，比如022Cr22Ni5Mo3N双相不锈钢。

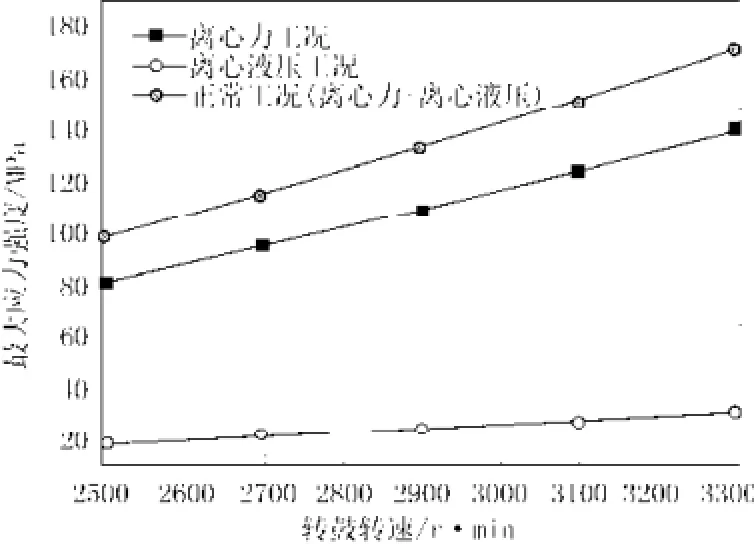
图1 转鼓最大应力强度随转鼓转速变化曲线Fig.1 The curve of the maximum stress intensity changing with rotating speed

表2和图2分别为最大径向位移随转鼓转速变化的数据结果和变化曲线。

由表2和图2可得，各工况下转鼓的最大径向位移均随着转鼓转速的增加而增加，特别是离心力工况和正常工况下的径向位移受转鼓转速的影响较为明显。因此，在增大转鼓转速时，应保证转鼓的径向变形量在刚度限制条件之内。

图2 转鼓最大径向位移随转鼓转速变化曲线Fig.2 The curve of the maximum radial displacement changing with rotating speed

轴向位移随转鼓转速变化数据和曲线此处省略。根据分析结果，各工况下的最大轴向位移均小于同样条件下的径向位移。轴向位移随转鼓转速变化的趋势与径向位移同转鼓转速的关系一致。在转鼓转速为3 300 r·min-1时，最大轴向位移值仍满足刚度条件。

表1 最大应力强度与转鼓转速(r·min-1)的关系Table 1 The relationship between the maximum stress intensity and drum speed

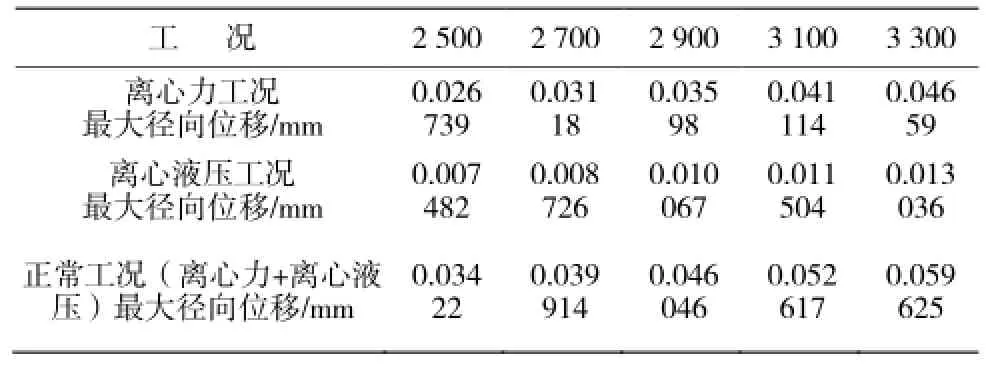
表2 最大径向位移与转鼓转速(r·min-1)的关系Table 2 The relationship between the maximum radial displacement and drum speed

2.2 转鼓壁厚对转鼓强度和刚度的影响

在转鼓的主要结构参数确定的条件下，转鼓的壁厚就成为影响转鼓强度和刚度的主要因素。当转鼓材料和加工成本一定时，壁厚越小，质量越轻，成本越低。LWS400卧螺离心机转鼓壁厚为15 mm，有较大的安全余量。因此，讨论转鼓壁厚对其强度和刚度的影响是对转鼓进行尺寸优化的必要条件。表3和图3分别为最大应力强度随转鼓壁厚变化的数据结果和变化曲线。

图3 转鼓最大应力强度随转鼓壁厚变化曲线Fig.3 The curve of the maximum stress intensity changing with the wall thickness

由表3和图3可知，在离心液压工况和正常工况下，转鼓的应力强度均随着转鼓壁厚的减小而增大，这说明转鼓壁厚对强度的影响主要通过物料离心液压对鼓壁的作用体现；离心力工况下转鼓的应力强度受转鼓壁厚的影响很小，说明壁厚的大小不对因转鼓自身质量产生的离心力引起的应力产生作用。当转鼓壁厚下降到6 mm时，最大应力强度数值已经超过了1.5Sm，根据表4中的数据，在当前操作工况（2 900 r·min-1）和转鼓选材（304不锈钢）的条件下，转鼓筒体壁厚可降至8 mm。

表3 最大应力强度与转鼓壁厚(mm)的关系Table 3 The relationship between the maximum stress intensity and wall thickness

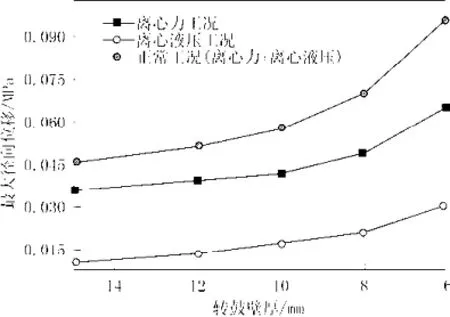
图4 转鼓最大径向位移随转鼓壁厚变化曲线Fig.4 The curve of the maximum radial displacement changing with wall thickness

表4 最大径向位移与转鼓壁厚(mm)的关系Table 4 The relationship between the maximum radial displacement and wall thickness

表4和图4分别为最大径向位移随转鼓壁厚变化的数据结果和变化曲线。由表4和图4可知，三种工况下的径向位移均随着转鼓壁厚的减小而增加且变化趋势非常相似；转鼓壁厚减小的越小，径向位移增大的速度越快。因此，通过降低转鼓壁厚实现转鼓经济性指标，应保证最大径向位移值满足刚度条件。

轴向位移随转鼓壁厚变化数据和曲线此处省略。根据分析结果，各工况下轴向位移均随着转鼓壁厚的减小而增大，其中离心力工况下的轴向位移的增长趋势缓慢，这说明减小壁厚不会使转鼓自身质量离心力产生的轴向位移有明显的增加。

根据以上分析，若将转鼓壁厚定位8 mm，可节省材料约28%，还可降低启动功耗。

2.3 液池深度对转鼓强度和刚度的影响

在转鼓内直径 Di一定的情况下，液池深度大，液相中的含固率降低，但过大的液池深度会使得固相中的含湿率过大无法满足产品要求；液池深度小，分离后得到的固相含水率低，过小的液池深度会增大排出固相的难度。因此，液池深度的选择应首先保证卧螺离心机能顺利排渣，再考虑固相的含湿量的要求。

液池深度的取值与转鼓内直径有关，根据文献［1］关于液池深度的取值范围，LWS400卧螺离心机的液池深度在 20～60 mm之间。以下分别讨论LWS400卧螺离心机液池深度在其范围内对转鼓强度和刚度的影响 。

表5和图5分别为最大应力强度随转鼓壁厚变化的数据结果与变化曲线。

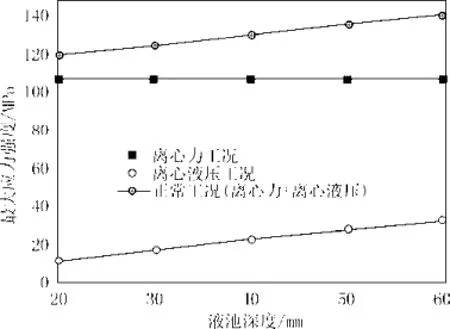
图5 转鼓最大应力强度随液池深度变化曲线Fig.5 The curve of the maximum stress intensity changing with liquid pool depth

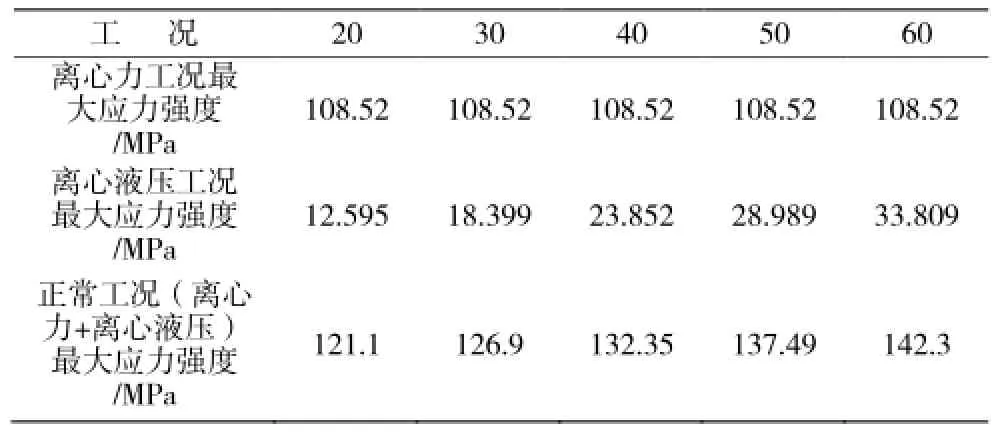
表5 最大应力强度与液池深度(mm)的关系Table 5 The relationship between the maximum stress intensity and liquid pool depth

由表5和图5可知，离心力工况下的最大应力强度不受液池深度取值的影响；离心液压工况和正常工况下的最大应力强度随着液池深度的增加而缓慢增加，当液池深度取最大值60 mm时，正常工况下的最大应力强度仍满足强度要求。因此，在LWS400卧螺离心机液池深度的选择过程中，可不考虑对转鼓强度的影响，只需保证满足相关工艺要求即可。

表6和图6分别为最大径向位移随液池深度变化的数据结果和变化曲线。

由表6和图6可知，液池深度对离心力工况下的径向位移影响极小甚至没有影响；另两种工况下的最大径向位移随液池深度的增加缓慢增大。

轴向位移随转鼓壁厚变化数据和曲线此处省略。根据分析结果，轴向位移同液池深度的关系与对径向位移的情况相同，即转鼓自身质量产生的离心力引起的轴向位移不受液池深度取值的影响，离心液压工况和正常工况下的轴向位移变化与液池深度的变化成正比。

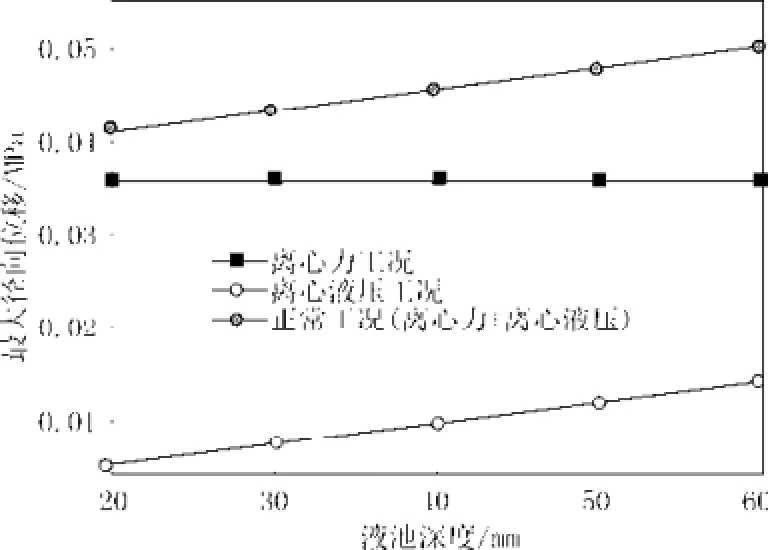
图6 转鼓最大径向位移随液池深度变化曲线Fig.6 The curve of the maximum radial displacement changing with liquid pool depth

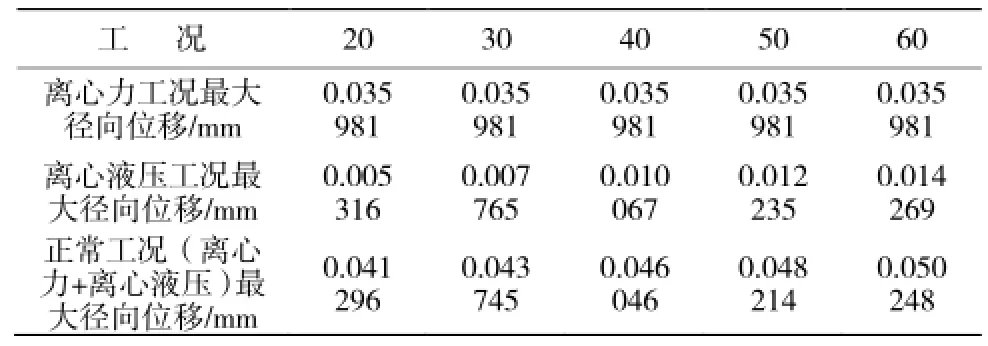
表6 最大径向位移与液池深度(mm)的关系Table 6 The relationship between the maximum radial displacement and liquid pool depth

3 结 论

（1）随着转鼓转速的增加或转鼓壁厚的减小，卧螺离心机转鼓的最大应力强度及变形量增加趋势非常明显；在保证LWS400卧螺离心机安全运行的前提下，设备可承受的最大转鼓转速为 3 100 r·min-1；允许的最小壁厚为8 mm。

（2）液池深度对转鼓自身质量离心力引起的强度和刚度结果不产生影响，在LWS400卧螺离心机中，液池深度的选择只需要保证工艺要求即可，可不考虑转鼓的强度和刚度条件。

（3）转鼓的径向变形量和轴向变形量受转鼓壁厚变化的影响极大，因此，在考虑转鼓经济性减薄转鼓厚度时需特别注意转鼓的径向、轴向变形量满足转鼓的刚度条件。

［1］孙启才, 金鼎五. 离心机原理结构与设计计算[M]. 北京：机械工业出版社, 1987.

［2］JB/T8051-2008 离心机转鼓强度计算规范[S].

［3］周知进, 傅彩明. 卧螺离心机转鼓主要参数对其模态影响的仿真[J].机械设计, 2006,23(9):28-30.

［4］高志惠, 黄维菊, 陈文梅. 大长径比卧螺离心机转鼓的有限元分析[J]. 过滤与分离, 2010,20(3):18-21.

［5］毛文贵, 刘迎春, 傅彩明. 卧螺离心机转鼓虚拟样机建模与有限元仿真研究[J]. 湖南工程学院学报，2005,15(4):44-47.

［6］王国强. 实用工程数值模拟技术及其在ANSYS上的实践[M]. 西安：西北工业大学出版社, 1999.

Influence of Parameters Changing of LWS400 Horizontal Spiral Centrifuge on the Strength and Stiffness of the Rotating Drum

LI Long
（Tianhua Institute of Chemical Machinery & Automation, Gansu Lanzhou 730060，China）

The geometric model for the drum of LWS400 Horizontal spiral centrifuge was established by using Solid Works software, and finite element analysis of the geometric model was carried out by ANSYS Workbench software. Effect of changing speed, wall thickness and liquid pool depth on the strength and stiffness of the drum was investigated, which could provide a reference for subsequent optimizing plans. The results show that the increase of rotational speed or the decrease of wall thickness has obvious effect on strength and stiffness of the drum. The change of liquid pool depth has little effect on strength and stiffness of the drum.

Horizontal spiral centrifuge; Drum; Finite element analysis

TQ 051

A

1671-0460（2014）11-2346-05

2014-04-10

李龙（1988-），男，甘肃张掖人，在读硕士研究生，研究方向：主要从事化工热能与动力设备研究。E-mail：f5bacon@163.com。