预应力风电机组基础锚杆笼连接计算方法研究

文／郭敏 谢超 谢治 申超

预应力风电机组基础锚杆笼连接计算方法研究

文／郭敏 谢超 谢治 申超

目前风电机组基础与上部塔架之间的连接多采用预制钢制基础环连接，如图1所示。然而随着风电机组容量的逐渐增大，基础环的局限性也表现得更加明显，因此一种新的连接方式－锚杆笼连接应运而生。锚杆笼连接在适用范围和建造成本上具有很大优势，然而由于其结构构成与常用的预制钢制基础环有显著差异，在设计与计算方法的选择上需要另辟蹊径。

锚杆笼连接理论

一、锚杆笼组成

锚杆笼主要由T型法兰、预应力锚杆和底环三部分组成，如图2所示。其中T型法兰直接与上部风电机组塔筒连接，T型法兰下方为高强灌浆，灌浆下方为基础混凝土；预应力锚杆提供固定上部塔筒的预紧力；底环嵌在混凝土基础中，用于固定预应力锚杆。

因此，锚杆笼连接设计和计算的关键参数即为：T型法兰受力、高强灌浆中应力、灌浆下混凝土中应力、锚杆应力以及底环应力。

二、设计与计算方法分析

（一）荷载分析

基础作为一个系统，在分析受力时，首先应该确定所选用的荷载。进行塔架与基础连接分析时采用的荷载由以下部分组成：沿着塔架圆周线的竖向荷载N和嵌入法兰层面处的弯矩M。

风电机组基础同塔筒法兰的连接方式为T法兰连接，左右两边对称。根据“材料力学（孙训方等）”可以分别推导出竖向力N和弯矩M对单个锚杆或者锚杆孔所占法兰面积施加的力，其中最大拉力和最大压力如式(1)和(2)所示：

最大拉力：

最大压力：

式中：M——塔筒传递到基础上弯矩；

N——塔筒传递到基础上竖向力；

Na——锚杆或锚杆孔总数；

D——锚杆平均分布直径。

（二）连接理论分析

锚杆笼连接中，首先需要确定锚杆预应力。锚杆预应力的确定原则是保证塔筒连接不脱开。从式(1)可以推出上部塔筒对单个锚杆所占法兰面积产生的最大拉力，而锚杆预应力的确定就依据该项结果。考虑到对金属材料施加预应力后，预应力会产生即时损失和随时间变化的损失，因此在用式(1)计算出单根锚杆所需要的预应力时还必须乘以一个放大系数以考虑预应力损失。由中船重工713研究所提供的泰普预应力锚杆的预应力损失有以下各项组成：材料本身的预应力损失约3%，混凝土徐变及温度变化对预应力的影响约3%，其它约5%，因此整体的预应力损失百分比为11%。

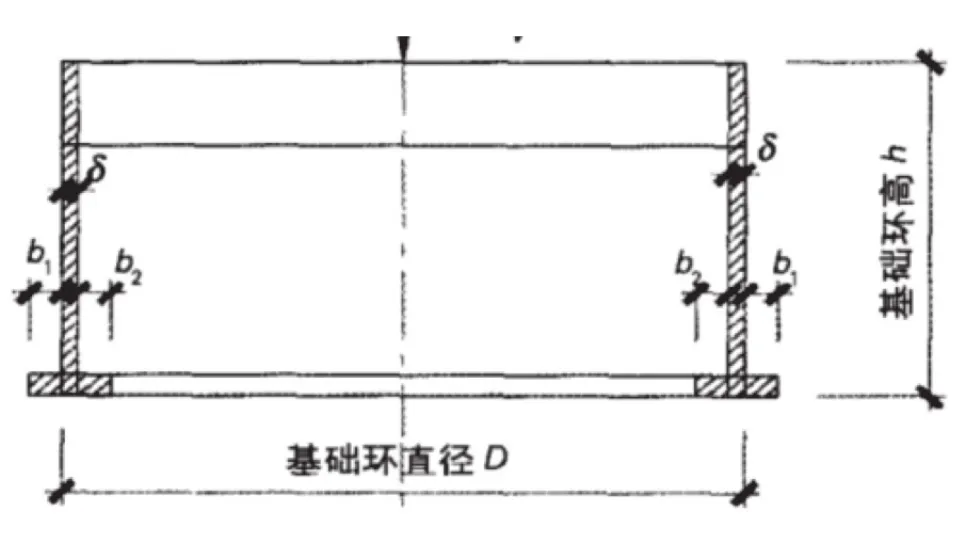
图1 基础环示意图

法兰下高强灌浆中的应力分析对塔筒荷载是否能够顺利传递到混凝土基础中十分关键。从图2(b)和图3中可以看出法兰高强灌浆在受压侧要承受很大的压应力，其计算过程如式（3）－（5）所示：

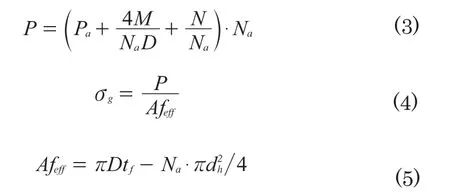
式中：Pa——锚杆预应力；

Afeff——法兰有效截面面积；

tf——法兰宽度；

dh——法兰上锚杆孔径。

灌浆下混凝土受力分析原理与灌浆中应力分析类似，但有效受压截面面积为灌浆底部截面面积，即：

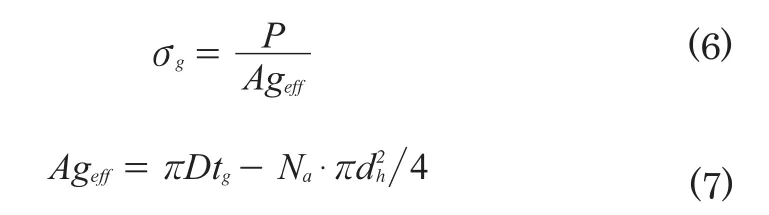
式中：Ageff——灌浆有效截面面积；

tg——灌浆底部宽度。

对灌浆下混凝土的受压分析结果，往往显示混凝土的抗压强度是不够的，这时需要根据“GB50010－2010混凝土结构设计规范”中局部受压承载力一节进行相应钢筋配置以保证局部抗压。

此外底环和T法兰的受力情况也是设计中需要考虑的重要项目。关于底环受力分析，选取相邻锚杆间底环段为隔离体，并视作两端固结梁。荷载采用锚杆最大拉力对底环上混凝土的压应力，根据结构力学相关知识，可以求解得到隔离体中中最不利截面位置以及最不利弯矩、剪力。T法兰受力分析与底环类似，仅选用荷载换成法兰下灌浆中最大压应力。

计算结果与分析

一、计算参数

本文以某风电场2MW风电机组为例，进行塔筒与基础的连接计算。该风电场风电机组采用的荷载如表1所示，荷载坐标系如图4所示。

锚杆笼示意图如图2所示，计算所需相关尺寸如下：

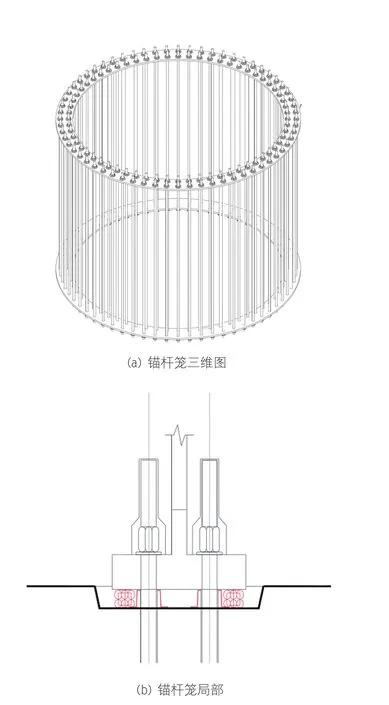
图2 锚杆笼示意图

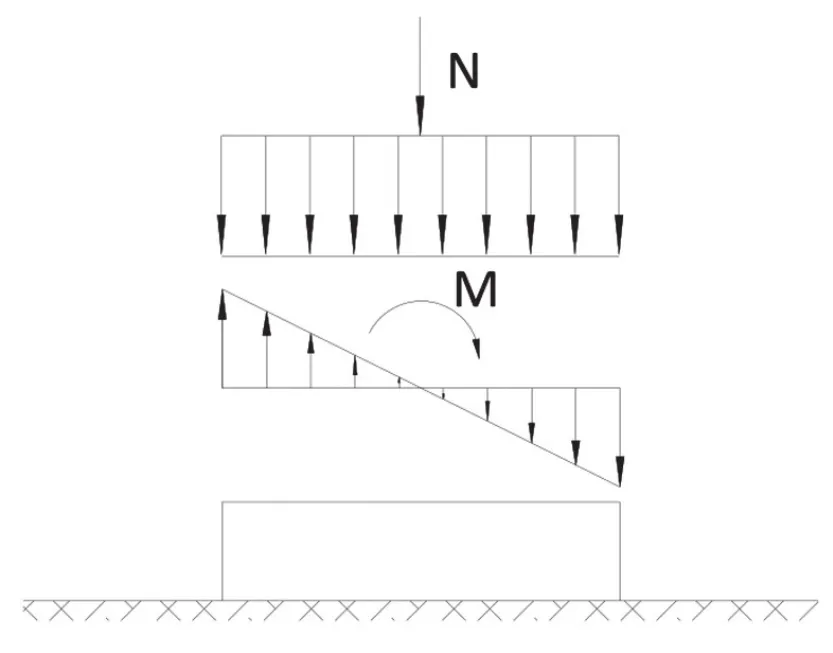
图3 锚杆笼连接采用的荷载

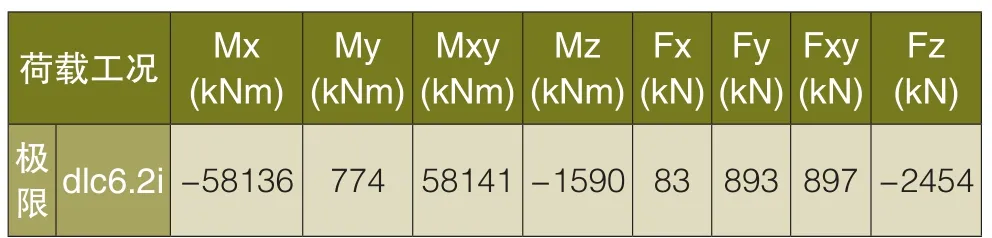
表1 计算采用荷载（不包括安全系数）

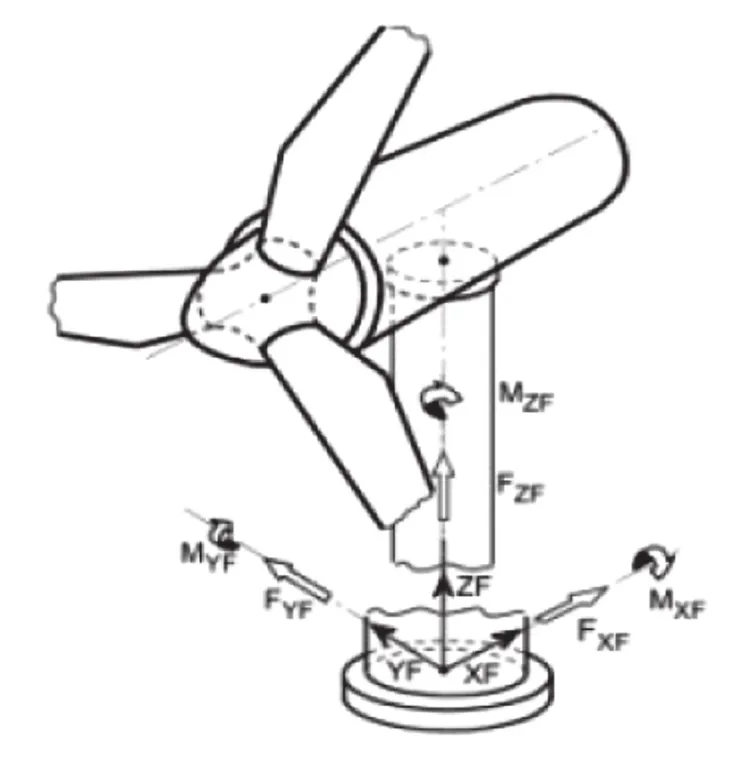
图4 荷载坐标系

法兰外径：4650mm，法兰内径：3890mm，法兰厚度115mm；

底环外径：4650mm，底环内径：3890mm，底环厚度50mm；

灌浆槽底外径：4730mm，灌浆槽底内径：3810mm，灌浆厚度70mm；

外圈锚杆分布直径：4458mm，内圈锚杆分布直径：4082mm，锚杆总数：120。

计算中所用材料如下：

高强灌浆C80，混凝土C40，底环和法兰为Q345C钢。

二、计算结果分析

根据上文，采用理论方法计算出来的结果如表2所示，其中锚杆预应力确定采用考虑修正系数的极限荷载标准值，其它项目的计算采用极限荷载设计值，荷载分项系数参考“FD003－2007风电机组地基基础设计规定”选取。

从表2看出，灌浆、法兰和底环中应力都控制在设计强度范围内，然而混凝土中应力大于设计抗压强度，需要配置局部受力钢筋。计算中锚杆所需最小预应力为646.67kN，但是最后采用的锚杆预应力为700kN，其它各项的验算均是基于预应力为700kN。

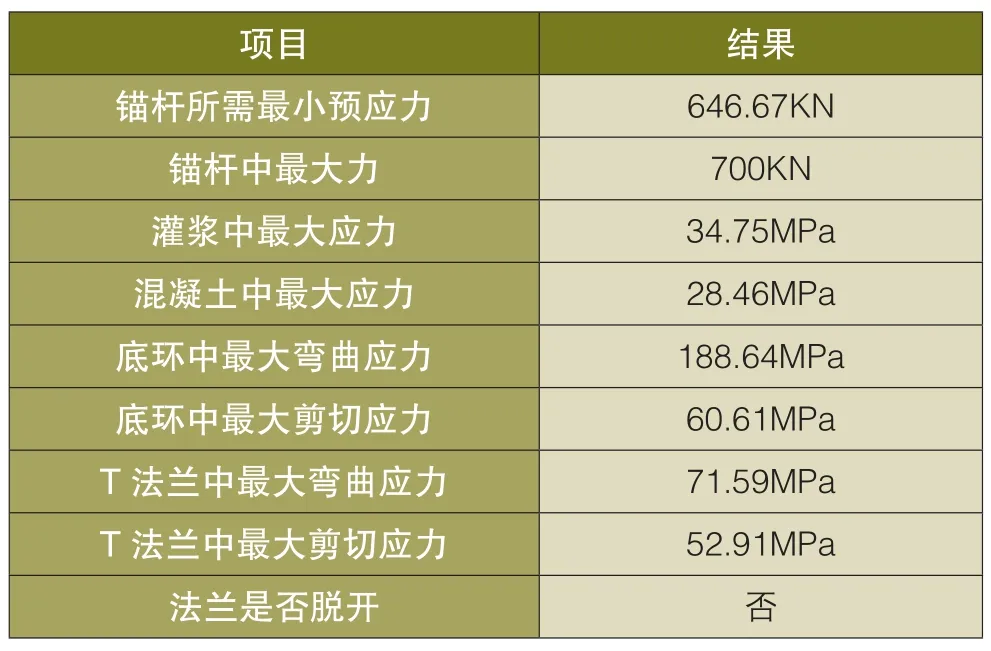
表2 理论方法计算结果

另外根据上文，灌浆和混凝土中最大压应力应出现受压侧最外边缘，底环和法兰中最大应力应出现锚杆孔附近。

三、有限元对比分析

为更全面研究锚杆笼连接的受力情况，同时采用有限元数值模拟进行对比分析。计算模型如图5所示。模型中将混凝土承台底面作为嵌固端，不考虑地下基础变形的影响；在法兰和灌浆料，法兰和螺母之间设置了接触对单元；通过预紧力单元给每根锚杆施加了700kN预紧力；简化模型，消除应力集中，螺母厚度与垫片相同；为了消除边界效应，建立了1.5m高的塔筒，并将塔筒顶部节点与坐标原点绑定，并在坐标原点施加荷载。

法兰与灌浆料的相对变形(放大100倍)如图6所示。从图中看出法兰和灌浆之间并无出现脱开，与理论算法计算结果一致。

法兰、灌浆以及灌浆下混凝土的最大受力情况如图7所示。

由图7(a)可知，法兰中最大Miles应力值出现在受拉端锚杆孔附近，且最大值为269MPa。而在理论算法中，选取的计算单元是假定最大应力出现在受压端锚孔附近，且求解出的最大弯曲应力为71.59MPa，最大剪切应力为52.91MPa。理论方法的计算结果与有限元分析结果有一定差异，因此在理论算法上需要改进使其结果更符合实际情况。

由图7(b)可知，灌浆中最大Miles应力出现在受压端灌浆槽边缘，且最大值为42.6MPa。理论算法中也是假定灌浆最大应力出现在受压端，且计算结果为34.75MPa。通过对比可知，理论算法中选取的简化方法是合理的，有限元结果中计算出的最大值偏大是因为理论算法并没有细致到考虑局部应力集中，是一种相对简化的算法。

图5 有限元计算模型

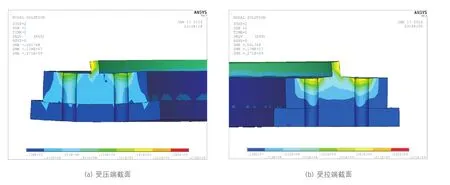
图6 法兰与灌浆料的相对变形

由图7(c)可知，法兰下混凝土中最大Miles应力出现在受压端锚杆孔附近，最大值为26.7MPa，但是并没有像灌浆那样出现应力集中现象。理论算法中也是假定混凝土最大应力出现在受压端，且计算结果为28.46MPa。两者计算结果比较接近，理论算法是一种合理的简化算法。

锚杆中最大受力情况图8所示。从图中看出，锚杆中最大应力为443MPa，最大力为704.20kN。有限元分析结果比理论计算结果略大，这是由于理论计算方法采用的简化。理论方法为简化计算，认为法兰脱开之前锚杆中应力保持为预应力不变，只有产生脱开后锚杆中应力才会随外力发生变化。而该工程中并未产生脱开，因此理论结果偏小就是必然的，但是由于锚杆与周围混凝土相比刚度较小，其增大并不显著，这也与有限元分析结果一致。

结论

从计算分析结果可以得出以下结论：

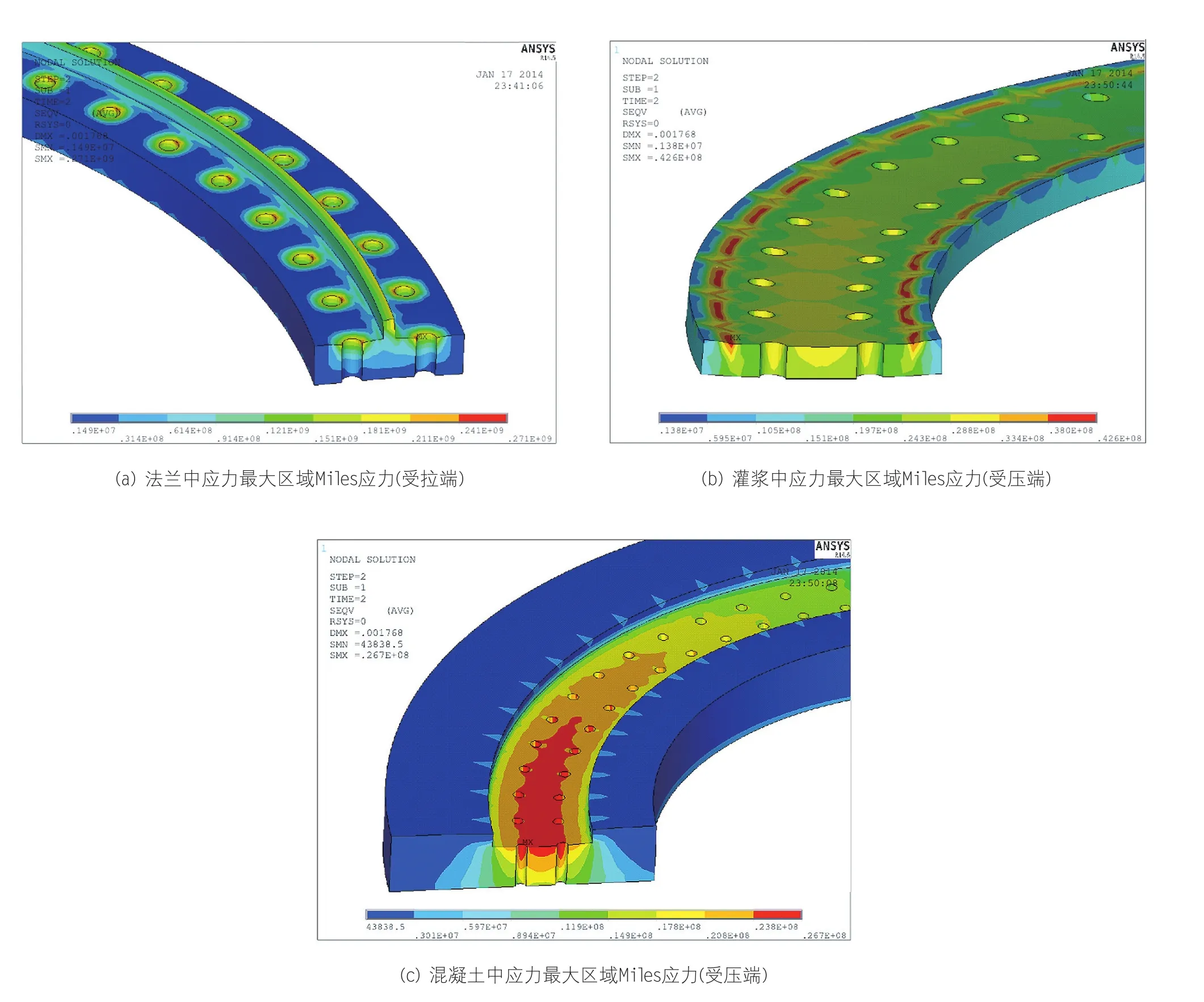
图7 法兰、灌浆和混凝土中应力最大区域Miles应力

图8 受拉端锚杆Miles应力

根据理论算法确定的锚杆预应力，可以保证法兰与灌浆之间不脱开，确保塔筒连接的稳定；

由于灌浆中易出现应力集中现象，灌浆中应力分布用理论算法计算出来的结果偏小，因此在设计中应该特别注意；

锚杆中应力变化和灌浆下混凝土中应力分布用两种方法计算的结果比较接近，理论算法可作为一种合理的简化算法；

法兰中应力分布，两种方法计算结果相差较大，理论算法不够准确，需要进一步探索更合理的计算方法。

（作者单位：郭敏：北京中水恒信环境科技发展有限公司；郭敏、谢超、谢治、申超：中船重工集团第七一三研究所）