GPS RTK测量精度的分析

郑建雷，刘国超，徐秀杰，张 晖，冯剑桥

（1.河海大学 地球科学与工程学院，江苏 南京210098）

RTK定位技术是基于载波相位观测值的实时动态定位技术，能够实时提供测站点在指定坐标系中的三维定位坐标，并达到cm级定位精度[1]。RTK测量模式只需要一台基准站接收机和一台或多台流动站接收机以及用于数据传输的电台。基准站通过数据链将其观测值和测站信息一起传送给流动站，流动站通过数据链接收来自基准站数据的同时自身也采集GPS观测数据，并在系统内组成差分观测值进行实时处理，得到cm级的定位结果。

GPS RTK测量精度大多能达到如下精度：水平精度1 cm+2×10-6，垂直精度2 cm+2×10-6。至于仪器的性能，则要看品牌。本文通过实验的形式，对影响RTK测量精度的一些因素进行定性分析，提出了提高RTK测量精度的方法和措施。

本文实验所用到的仪器有：RTK接收机为TRIMBLE R8，水平精度±10 mm+1×10-6；垂直精度±20 mm+1×10-6；初始化时间一般小于10 s；初始化可靠性大于99.9%。全站仪为LEICA TM30，其测角精度为0.5"，测距精度为±0.5 mm+1×10-6。

1 卫星的几何形状和高度角对定位精度的影响

一般来说，可视卫星数目的增加会获得更好的精度结果[2]。综合考虑大气折光与高度角的关系以及高程解与钟差解的相关性[3]，当一颗卫星靠近天顶，其余卫星之间相距近似120°时，所构成的卫星几何图形最佳，此时的GDOP值也是较小的。

从图1、图2可以看出，图1的卫星几何形状明显优于图2，而且图1的GDOP值也明显的小于图2，故由图1的卫星几何形状所获得的定位精度会优于图2。

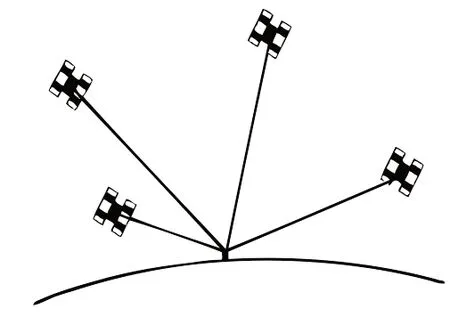
图1 卫星几何形状图（GDOP较小）

图2 卫星几何形状图（GDOP较大）

从图3、图4可以看出，平面和高程精度在高度角较大的时候要好。这可能是由于随着高度角的提高而“筛掉”了部分卫星的结果，造成可视卫星的GDOP值也因此而发生变化。

图3 高度角不同的平面精度

图4 高度角不同的高程精度

因此，在进行外业观测前，应事先对当天的观测情况作一些大致的了解和预测，以便更好地进行外业观测的设置。选择合理的卫星几何形状，构成最佳几何图形，并选择适当的高度角，对RTK定位精度的提高有很大的帮助。

2 浮点解对定位精度的影响

浮点解是当模糊度参数取实数时所求得的基线向量解，也称实数解。由于RTK自身系统的缺陷和流动站周围环境的影响，有时候在用RTK进行定位时难免会出现解的精度不高或浮点解的情况[4]。这主要是因为GPS信号不好、卫星状况不佳或视场内障碍物过多时整周模糊度解算不成功导致的，此时得到的解称之为浮点解。

本文在信号不好的点位（树荫下、房屋边上）用RTK进行数据采集，在只能获得浮点解的情况下，对采集到的点位坐标进行精度分析。使用RTK采集的浮点解的坐标数据，其点位的平面误差和高程误差都是直接由流动站手簿获得，即浮点解自身的精度。用LEICA TM30全站仪对12个实验点进行测量（忽略全站仪测量误差，将其作为真值），然后用RTK测量这12个实验点，将其与全站仪坐标值进行比较。如表1所示。

表1 TM30与RTK坐标精度对比/m

从表1可以看出，浮点解的点位误差无论是平面还是高程都较大，点位误差最大的G11点的平面精度为17.8 cm，高程精度为41.2 cm，点位误差最小的G04点的平面精度为14.6 cm，高程精度为20.2 cm。由此可见，由RTK浮点解解算得到的点的点位误差都是比较大的，其精度不能满足一般的工程测量要求。

由于RTK浮点解是在解算整周模糊度未知数时出现了问题而产生的，所以要想提高RTK测量的精度，就必须对整周模糊度的解算过程有一个较详细的了解，选用一种能快速正确解算出整周模糊度的方法。

3 流动站到基准站距离对定位精度的影响

一般情况下，流动站到基准站之间距离较短时，可以通过观测值的差分处理来削弱其残差影响；当流动站到基准站之间的距离较长时，GPS误差的空间相关性将随着站间距离的增大而逐渐失去线性关系。因此在2者距离较长的情况下，经过差分处理后的流动站的数据仍然含有较大的观测误差，从而容易导致定位精度的降低与无法解算整周模糊度[5,6]。

为研究流动站到基准站距离对RTK定位精度的影响，分别研究5 km、10 km、15 km、20 km、25 km范围内RTK测量精度。在0～5 km、5～10 km、10～15 km、15～20 km、20～25 km、25 km范围外各选取5个实验点，共30个实验点。先用GPS静态测量方式得到这30个点的坐标值，然后再用RTK测定其坐标值。点位精度如图5所示。

图5 RTK定位精度与基线长

从图5中可以看出，点位的最大平面误差为5.2 cm，该点距离基站30 km；最小平面误差为1.8 cm，距离基准站3 km。在10 km范围内坐标随距离的变化较小，曲线平缓，精度较高，在10 km范围内平面精度基本上可以达到2.4 cm的精度。随着基线长度的增大，点位误差的精度有所降低，这主要是由于流动站与基准站的误差空间相关性有所减弱而造成的。就目前来说，流动站与基准站间是通过电台模式作业的，为了达到稳定可靠的数据，2者间的距离最好是控制在10 km以内（主要还得看地理环境、周围的干扰程度等）。

4 坐标转换对定位误差的影响

坐标转换参数的求解是GPS RTK测量的关键所在，因此在对转换参数进行求解时，尽量使用高等级的控制点作为转换公共点。一般来讲，平面转换所需的控制点至少2个，分布尽量均匀，能涵盖整个测区，且相邻控制点之间距离应为3～5 km，以确保拟合精度要求[7]。

求解坐标转换参数的一般方法是：在测区内选取3个以上待使用已知点（最好均匀分布在整个测区），采用静态同步观测的方法，使用数据处理软件对以上待使用已知点，在WGS84坐标系统下进行基线的解算和网平差，求出每个已知点精确的WGS84坐标，采用点校正，求出坐标转换参数。值得注意的是，在测区范围较小、已知点较少且分布不均匀时，也可不求转换参数直接进行测量，缺点是控制范围不大，容易引起坐标转换误差。转换参数也有它的使用范围，在一定区间内求解的转换参数只能用在控制点的附近和内部，而不能在其他测区使用[8,9]。

本文为验证转换参数对RTK定位误差的影响，采用以下2种方案。方案1：以CG01、CG05、CG06三点作为已知点求解转换参数；方案2：以CG02、CG03、CG04 三点作为已知点求解转换参数。其中CG01、CG05、CG06为 二 等GPS控 制 点；CG02、CG03、CG04为3等GPS控制点，其余的为4等GPS控制点。控制点的分布如图6所示。

图6 点位示意图

表2 方案1精度表

表3 方案2精度表

由表2、表3可以看出，由方案1求解的转换参数得到的点位误差优于方案2，这可能与公共点的精度和分布有关系。CG01、CG05、CG06为一等GPS控制点，其精度比 CG02、CG03、CG04 高，而且CG01、CG05、CG06分布在测区内部，可以很好地控制整个测区。与此同时，坐标转换期间待测点坐标的精度存在着坐标转换的损失。经验表明，这种损失一般在1 cm左右，这也与公共点的精度和分布有关。所以公共点的选择直接影响到了坐标转换成果的好坏，进而影响RTK测量的精度。公共点应为高等级控制点，均匀分布且涵盖整个测区，这对提高RTK测量精度都有很大帮助。

5 结 语

RTK作为新一代测量的最新技术，其自身也存在一定的局限性，这限制了RTK测量的可靠性和精度。本文以实验算例的方式对影响RTK定位精度的各因素进行了分析，得到以下结论：①选择合理的卫星几何形状和高度角，对于提高RTK测量精度有很大帮助；②对于观测条件比较差的地段，可以适当增加观测时间，有利于提高RTK测量精度；③通过电台模式作业的RTK，应尽量缩短流动站与基准站间的距离，以提高RTK定位精度和稳定性；④选取高等级、均匀分布的公共点对提高坐标转换参数的精度有很大的帮助。

[1]陈小军.利用GPS(RTK)进行工程放样、界址点测量及其精度分析[D].武汉:中国地质大学,2012

[2]丁仁军，倪曙.影响网络RTK精度的相关因素分析与研究[J].地矿测绘,2009,25(1):19-22

[3]胡友健，罗昀，曾云.全球定位系统（GPS）原理与应用[M].武汉：中国地质大学出版社，2008

[4]邓明镜.RTK浮动解精度分析[J].测绘通报,2010(增刊):116-118

[5]Hu G R, Khoo H S, Goh P C et al.Development and Assessment of GPS Virtual Reference Stations for RTK Positioning[J].Journal of Geodesy,2003, 77:292-302

[6]Dai L, Eslinger D, Sharpe T, et al.Innovative Algorithms to Improve Long Range RTK Reliability and Availability[C].ION NTM 2007, San Diego, CA,2007

[7]赵萌.GPS-RTK测量精度的分析与质量控制[J].铁道勘察,2012(2):10-12

[8]王锴华，徐爱功.基于单基站CORS的RTK精度与距离测试[J].矿山测量,2012(1):29-32

[9]张孝军，林云发.GPS RTK技术的测量精度探讨[J].人民长江,2005,36(10):46-48