离散数据地球化学编图中克里格法的应用—以津巴布韦超低密度地球化学图为例

张燕，张素荣

（中国地质调查局天津地质调查中心,天津 300170）

离散数据地球化学编图中克里格法的应用—以津巴布韦超低密度地球化学图为例

张燕，张素荣

（中国地质调查局天津地质调查中心,天津 300170）

自由网离散数据的地球化学编图以任意方式进行网格化成图存在明显不确定性，会导致地球化学特征的改变或歪曲。克里格法提供了一种更科学合理的空间估计插值方法。笔者运用该方法对津巴布韦超低密度地球化学调查数据进行了空间分析并编制了地球化学图件，研究和讨论了自由网离散数据的地球化学编图方法，评价了采用克里格法编制地球化学图的效果。

编图方法；克里格法；变差函数；津巴布韦；地球化学图

地球化学等值线图的应用非常广泛，通常是对地球化学填图形成的数据进行网格化插值来实现的。地球化学编图所依赖的数据分布及其结构特征对图件编制有重要影响。目前对自由网地球化学数据的插值估计大多采用了距离倒数加权插值法,其在算法上比较简单,但是没有考虑到数据点间的空间相关性和合理的半径,计算和编图结果一般是不确定的，甚至可能是错误的。自由网地球化学数据的插值估计形成的曲面应能最好地拟合实测数据。地球化学调查数据的空间变化规律应从数据本身分析，研究数据变化的每个变量的拟合变差函数的信息。地球化学调查数据的插值估计通常可以采用克里格法，这是一种有效的空间估计插值方法，在很大程度上依赖于数据模型的空间相关性。

本文以津巴布韦低超密度地球化学图的编制为例，对离散数据的区域地球化学等值线图编图方法进行了探索和研究，编制了一套自由网离散数据条件下的区域地球化学图，并对克里格法的效果及其合理性进行了讨论。

1 克里格法的基本原理

克里格插值（Kriging）是建立在变异函数空间分析基础上，对有限区域内的区域化变量取值进行无偏最优估计的一种方法[1]。这是1951年南非采矿工程师D.G.K rige提出的对矿体品位和储量的一种估值方法。1971年法国地统计学家Matheron把这种方法命名为Kriging，并在此基础上提出了区域化变量理论，使传统的地学方法与统计方法相结合，理论化、系统化，形成了完整的方法体系。

1.1 克里格插值的关键问题

克里格法的基本原理是根据相邻变量的数值，利用变差函数所揭示的区域化变量的内在联系来估计空间数值。按照空间场是否存在漂移可将克里格法（Kriging）分为普通Kriging法和泛Kriging法,其中以普通Kriging法在地球化学编图中最为常用。

克里格插值是根据待插值点与其临近实测数据点的空间位置，对待插值点的变量值进行无偏最优估计，通过生成一个关于区域化变量的克里格插值来表达研究区域的原始数值，其基本公式为式如下：

式中：Z（x0）表示未知样点的值；Z（xi）表示未知样点周围的已知样本点的值；N为已知样本点的个数；λi为第i个样本点的权重，但权重一般并非距离倒数的权重，而是某种拟合数学模型。它的确定可以通过半方差的分析获取，根据统计学上无偏和最优的要求，利用拉格朗日极小化原理，可推导出权重值和半方差之间的公式[2]。

从求解估计值Z(X0)的过程可见，Kriging插值的关键是如何获取变差函数的最佳计算公式。这涉及两个主要问题,变异函数理论模型的选取和模型参数的估计[3]。

1.2 半方差函数

所谓半方差函数γ(h)就是两点间差值方差的一半，是用来描述地球化学特性空间连续变异的一个连续函数，反映了不同距离观测值之间的地球化学特性的变化，也称为变异函数。它是地质统计学中研究土壤、岩石或水系沉积物地球化学数据特征值变异性的关键函数。其表示形式如下：

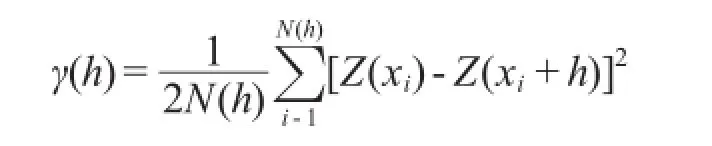
式中：γ(h)为实验半方差函数；H=xi+h，h为步长，即在一定方向上，距离为h的矢量；Z(xi+h)，Z(xi)为某变量的测定值；N(h)是以h为间距的所有观测点的成对数目。

总体来讲，距离愈近的已测点间和距离较远的已测点间相比，前者具有较小的平方差。每一样点对被划出后（分组后），就可以用一个模型来拟合它们。基于最小二乘法与最大似然法得到拟合最好的表面。理论上变异函数模型比较多,常用的有线性模型、指数模型、高斯模型和球状模型等[3]。有几个重要的参数可用来描述这些模型：块金值、基台值、自相关阈值（变程）。实际应用的时候可以在高级参数里面对其进行调整以减少误差方差。

2 工作步骤

克里格插值方法需要完成以下主要步骤：

（1）分析数据的分布特征，揭示数据的空间规律。对数据的分布进行分析，必要时进行数据转换，使数据符合正态分布的前提假设。正态分布转换能够改善插值结果。

（2）分析数据的空间变化趋势。总体上,可以近似认为变异函数存在几何异向性。进一步,需要将各向异性转化为各向同性[4]。

（3）确定变异方差的函数类型。生成变异函数和协方差函数，用于估算样点值间的统计相关（空间自相关）。变异函数和协方差函数取决于自相关模型（拟合模型）。分别采用线性模型、指数模型、高斯模型和球状模型进行拟合,确定影响方差变异函数分析有四个基本参数：块金（C0），基台(C0＋C)，变程（a）和方差变异函数类型（拟合模型）。这需要进行多次模拟运算，才能得到合适的结果。

（4）计算网格化的预测值。依据变程选择合适的搜索半径和临近数据点数，选取合适的插值方法进行网格化插值计算。

（5）结果分析和检验。对拟合的连续曲面上的估计值与实测值的方差进行检验。一般而言，如果克里格插值结果具有最小的方差，而且交叉检验中误差的方差最小，那么该结果就是合适的。

在通常所研究的空间尺度情况下，半方差函数值都随着样点间距的增加而增大，并在样点间距大于相关距离（a）时，该值趋于一个基本稳定的常数(C0＋C)。

3 应用实例-津巴布韦超低密度地球化学图的编制

（1）样品与数据

津巴布韦全国低密度地球化学调查的采样是根据津巴布韦全国地形地貌和水系分布，并结合交通条件，采用水系沉积物样品以超低的采样密度在高级别的水系或河流中系统布置和采集的（图1）。采样力求控制面积均等和兼顾样品分布的均匀性。采样密度按1个样品控制800～1000 km2的汇水面积，使每个采样点都能有效地控制相应的汇水面积。野外共采268件样品，实际控制30余万平方千米的面积。选用多种分析方法的配套方案，对41种元素和化合物进行了定量分析。获得了每个采样点的平面位置坐标、高程和41种元素的含量数据[5]。

（2）数据统计和变差函数模型的选择

津巴布韦超低密度区域地球化学调查数据的统计分析和变差函数模型的检验采用地统计学软件GS+7.0进行分析。通过计算机软件对数据的分布进行分析，分析数据的空间变化趋势，采用不同的变差函数模型进行拟合计算。选择决定系数（R）最大的模型，即选用的模型和参数对离散数据的拟合程度高，网格化计算出来的值与实际测量值的偏差最小。经过计算机处理和计算，41种元素最终采用的网格化变差函数模型类型为Ag、Au、Bi、Cao、Cd、Co、Cu、K2O、Li、Mo、Nb、P、Pb、Sb、Ti、W、Pt、Pt的变差函数为球状模型；A l2O3、Be、Cr、MgO、Ni等的变差函数为高斯模型；Zn、As、B、Fe2O3、Sn、V的变差函数模型为线型；Ba、F、Hg、La、Mn、Na2O、SiO2、Sr、Th、U、Y、

Zr的变差函数模型为幂指数型。其中部分元素的函数模型的参数计算结果见表1。

（3）图件编制

津巴布韦全国低密度地球化学图使用的软件版本为中地数码开发的MapGIS6.7软件，采用Kriging对离散数据进行网格化插值成图。根据变差函数模型的分析和检验，成图时对41种元素的变差函数模型分别采用高斯模型、球状模型、线形模型、幂指数模型等变差函数拟合模型。插值网格化间距依据数据最小间距确定为8 km；搜索半径依据各元素数据模型的变程确定，最大搜索半径100 km（图2～5）。

4 结论

（1）在克里格插值中，权重不仅考虑了已知点与插值点间的距离，而且考虑了己知点的位置和属性值整体的空间分布和格局，插值中的权重取决于已知点的拟合模型和已知点到插值点的距离以及插值点周围的已知样点的空间关系等多重因素。

（2）克里格分析方法需要一定的数据量，计算中的样本不够可能影响效果。克里格插值误差随块金值的增大而增大；基台值对结果影响不大，确定最佳变程值和最佳拟合函数是重要的，应选择决定系数

（R2）较高的函数。

图1 津巴布韦超低密度区域地球化学调查采样点位图Fig.1 Sam p ling loca tions o f the u ltra-low density regiona l geochem ica l su rvey in Zim babw e

表1 津巴布韦超低密度区域地球化学调查数据变差函数模型Table 1 Va ria tion func tion m ode lo f u ltra-low density regiona lgeochem ica l su rvey da ta in Zim babw e

（3）津巴布韦超低密度区域地球化学图件编制的效果是可以肯定的，总体上反映了区域地球化学背景特征的实际情况，清楚地指示了若干地球化学省、地球化学带的空间展布规律，为区域地球化学研究提供了可信的基础图件。

图2 津巴布韦Al2O3地球化学图Fig.2 Geochem ica lm ap o f Alum inum Oxide in Zim babwe

图3 津巴布韦K2O地球化学图Fig.3 Geochem ica lm ap of Po tassium Oxide in Zimbabwe

图4 津巴布韦B地球化学图Fig.4 Geochem ica lmap o f Boron in Zimbabw e

图5 津巴布韦Cr地球化学图Fig.5 Geochem ica lmap o f Chrom ium in Zim babwe

[1]侯景儒，黄竞先.地质统计学的理论与方法[M].北京:地质出版社，1990.

[2]王艳妮，谢金梅，郭祥.ArcGIS中的地统计克里格插值法及其应用[J].软件导刊，2008，7(12):36-38.

[3]曾怀恩,黄声享.基于Kriging方法的空间数据插值研究[J].测绘工程，2007，16(5):5-13.

[4]孙洪泉.地质统计学及其应用[M].北京:中国矿业大学出版社，1990.

[5]Gengxin Zhao，Fuqing He,etal.Ultra-low density geochemicalmapping in Zimbabwe[J].Journal of Geochemical Exploration，2014.

Abstract:Theweightsof evidencemodel isan importantmethod for themetallogenetic prognosis.It isa statisticalmethod of geoscience based on two valued image.The metallogenetic prognosis based on GIS using the weights of evidencemodel can be done through overlaying the informations of geoscience related w ith them ineral resources.Themetallogenetic prognosis based on GIS using theweightsof evidencemodel is based on the data,and realized easily.Using datum in North Daxinganling,weights of evidence predictionmodel of gold show preferred precision for predictingm inerals resources.Information to create new preferable compositive variables was integrated using theARCGISsystem.

Key words:GIS;weightof evidencemethod;metallogenetic prediction;evidence layer

更正

本人及合作者在本刊2012年第2期发表的《华北克拉通南缘洛峪群－汝阳群属于中元古界长城系—河南汝州洛峪口组层凝灰岩锆石LA-MC-ICPMSU-Pb年龄的直接约束》一文中，由于我们的测年材料为左景勋等（1997）文章所报道汝州阳坡村附近洛峪口组内的夹层状层凝灰岩，并误以为我们所观察剖面就是他们文章报道的“阳坡剖面”，因此在拙文中直接引用了他们的剖面图，并根据我们的观察和区域资料，将其上覆层位的时代归属由原来的“寒武系”修改为“震旦系”。最近，经与左景勋先生交流并再次观察后确认，我们这一修改其实有欠妥之处。实际上，拙文所报道的测年剖面是近年新开劈的通往阳坡村的乡村公路，位于左景勋等（1997）“阳坡剖面”的东侧。虽然两者相隔不足千米且完全平行，但由于两条剖面的起点及终点位置毕竟不同等原因，拙文的剖面顶部及附近地层为“震旦系”，与左景勋等（1997）所报道“寒武系”应有所不同。特此更正并向左先生及其合作者、向广大读者以及《地质调查与研究》编辑部致歉！

苏文博（中国地质大学（北京）地学院）

2014年12月3日

Application of K rigingon Geochem icalM appingM ethod w ith DiscreteData:Illustrated by theU ltra-low Density Geochem icalM apping in Zimbabwe

ZHANG Yan,ZHANG Su-rong
(Tianjin Center,ChinaGeologicalSurvey,Tianjin 300170,China)

There are obvious defects and uncertainty on the geochem icalmapping w ith freemeshing and discrete data by grid interpolation.Itwill lead that thegeochem ical characteristics are changed or distorted.Krigingmethod provides amore scientific and reasonable interpolationmethod forestimating the data.We discuss the application of the Kriging method on the geochem icalmappingmethod w ith discrete data by spatial analysis and geochem icalmapping of ultra-low density geochem ical data in Zimbabwe,and assessed the effect of application about the Krigingmethod in thegeochem icalmapping.

mapping;Kriging;variation function;Zimbabwe;geochem icalmap

MineralResources Evaluation of Comprehensive In form ation by Weightsof EvidenceM ethod in North Daxingan ling A rea

TENG Fei,ZHANG Yan,ZHANG Su-rong,XING Yi
(Tianjin Center,ChinaGeologicalSurvey,Tianjin 300170,China)

P628

：A

：1672－4135（2014）04－0283-05

2014-09-02

中国地质调查局承担的中国与津巴布韦的合作项目（商援[2007]573号）

张燕（1962-），女，工程师，1988年毕业于西安地质学院制图专业，现从事地质信息专业，Email:1342052428@qq.com。