一种高效的GNN查询算法的研究

黄 凯

（福建省特种设备检验研究院泉州分院，福建 泉州 362000）

一种高效的GNN查询算法的研究

黄 凯

（福建省特种设备检验研究院泉州分院，福建 泉州 362000）

给定集合P和Q，则GNN查询返回的是P中的对象p，p满足到Q中所有对象的距离的集合函数f最小。求GNN的方法有多种，文章提出了vp-GNN算法，其特点在于不采用任何索引的情况下，也能高效地对空间数据库中的数据进行裁剪，缩小查询区域、提高GNN的查询效率。

空间数据库；最近邻；集合最近邻

1 背景

数据挖掘（Data Mining）是指从大量的、不完全的、有噪声的、模糊的、随机的实际应用中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。它实质是一种知识发现的过程。[1]

在数据挖掘中，相关性查询是一种极为重要的查询问题。通常情况下，人们在研究两个对象之间的相关性时，都用对象之间的距离来衡量。在大量的数据中，尤其是在空间数据库中，最近邻查询就经常被用于求两个对象之间的相关性。然而要在整个空间数据库中求最近邻并不是一件容易的事，它需要花费大量的时间和空间。因此为了减少查询所需要的时间以及缩小查询的空间范围，人们引进了各种各样的空间索引[2]，如：R-tree、R*-tree等。

集合最近邻查询[3]是空间数据库中一种新的查询方法，其实质是从最近邻查询方法中演变而来的。但是因为集合最近邻查询的查询点是多个而不像最近邻查询那样查询点只有一个，因此它比最近邻查询要复杂得多。常见的GNN[4]方法有MQM、SPM、MBM[5]等，它们基本能够很好的解决低维空间数据库的GNN查询问题。不过，它们基本都是通过借助“索引”来对空间数据库进行裁剪，这往往会因为索引本身的极限性而影响GNN算法的效率。

2 vp-GNN算法

在接下来的讨论中，假设空间数据库为二维的；假设对象之间的距离用欧氏距离表示，不考虑对象本身可能带有的权值；并且假设集合函数f为求和函数sum。不过，这不能就说明接下来讨论的方法就只适合满足上述假设条件的查询，它们同样适用于多维空间数据库和f是其它单调递增的集合函数。

2.1 算法的基本思想

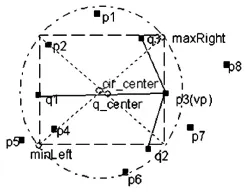
图1 最小包围矩形的外接圆

这种方法在集合P和Q都均匀分布在欧氏空间的情况下，一般都能找到正确结果，但是并不能证明落在区域内的候选点一定就是GNN查询的结果，也可能存在某一点，其中，但满足，也即虽然 落在裁剪区域之外，却为GNN查询的结果。因此就有必要将裁剪所得的区域进行放大，这在更新的vp-GNN算法中将进行了讨论。

另外，在vp-GNN方法中需要求查询集合Q的质心q_center。质心的求解公式如下：

不过，虽然公式（1）和公式（2）求解的质心精确度很高，但它只适合于当的空间数据，当n＞2时，它就不再是一个好的方法了。为了解决n＞2时高效的求Q的质心的问题，人们引入了一种通过降低质心的精确度，来降低计算的复杂度的方法。引入的求质心的新公式如下：

2 . 2 算法流程

（2）求查询集合Q的质心q_center；

（3）求q_center在被查询集合P中的最近邻vp；

（5）求MBR的外接圆的圆心；

（6）求MBR的外接圆的半径；

（8）在裁剪区域R中求GNN的结果。

2.3 算法的复杂度

（1）从时间复杂度方面讲，求Q的质心q_center的时间复杂度为O（n），其中n表示Q中包含的点的个数；而在求q_center在P中的最近邻时，它的时间复杂度为O（N），其中N表示P中包含的点的个数；求最小包围矩形MBR的左上顶点和右上顶点的时间复杂度为O（n+1）；在计算MBR的圆心和半径的时间复杂度都为O（1）；对集合P的裁剪的时间复杂度为O（N）；在裁剪区域R中求GNN的结果的时间复杂度最大不会超过O（N）。又因为集合P中具包含大量的数据点，一般远远大于Q的中的点，所以vp-GNN算法的时间复杂度为可近似的表示为O（N）。

（2）从空间复杂度方面讲，vp-GNN算法中主要的空间消耗是在于集合P、Q和R。因为集合R一般都会小于P，最坏情况等于P，而集合Q是会远远小于P，因此vp-GNN的空间复杂度也可近似的用O（N）表示。

3 改进的vp-GNN算法

3.1 算法的基本思想

3.2 算法流程

（2）求查询集合Q的质心q_center；

（3）求q_center在被查询集合P中的最近邻vp；

（5）求MBR外接圆的圆心和半径r；

（7）求出新的裁剪区域C(o,г＇)，并令R= C(o,г＇)；

（8）在裁剪区域R中求GNN的结果。

3.3 算法核心代码

3.4 算法的复杂度

（1）因为更新后的vp-GNN方法只是将vp-GNN方法的裁剪区域的半径进行放大，并没有其他额外的操作，因此它在时间复杂度方面与vp-GNN的时间复杂度是一致的，即也近似等于O（N）。

（2）另外，由于更新后的vp-GNN方法放大了裁剪区域的半径，所以整个裁剪后的区域会比vp-GNN方法裁剪去来的区域来得大，因此更新后的vp-GNN的空间复杂度会比vp-GNN的空间复杂度高些。但是因为裁剪后的区域R仍然不会大于集合P，所以同样可以用O（N）来表示更新后的vp-GNN的空间复杂度。

4 结束语

当集合P固定时，不管是集合Q中点的个数、集合Q的区间大小、还是空间数据库的维数的高低都会影响裁剪区域中所包含的点的个数。并且当集合Q中点的个数越多、或集合Q的区间大小越大、或者空间数据库的维数越多时，裁剪出来的区域所包含的点的个数也就越多。但是从求取GNN所需要的CPU时间方法来看，能够得到不管vp-GNN裁剪出来的区域是怎么样的，它们都比MQM方法所需要的CPU时间来得短。

文中提出的改进的vp-GNN算法，虽然较传统算法效率要高，但在衡量两个对象之间的相关度，还简限在用欧氏距离来表示。文章今后的研究方向将加入对对象本身带有的权值、对移动对象的查询以及对高维的空间数据库等方面的考虑，使得该算法能更好地应用于工程实践。

[1] Jiawei Han, Micheline Kamber著，范明，猛小峰，译.数据挖掘概念与技术（第二版）[M]，机械工业出版社，2007.3.

[2] Z. Song and N. Roussopoulos. K-Nearest Neighbor Search for Moving Object[J]. In VLDB 2001: 287-298.

[3] Papadias, D., Tao, Y., Mouratidis, K., Hui, C.K.: Aggregate Nearest Neighbor Queries in spatial database[J]. ACM Trans. Database Syst. 30(2) 2005: 529-576.

[4] Li, H., Lu, H., Huang, B., Huang, Z.: Two Ellipse-based Pruning Methods for Group Nearest Neighbor Queries[J]. In: GIS 2005: 192-199.

[5] Papadias, D., Shen, Q., Tao, Y., Mouratidis, K.: Group Nearest Neighbor Queries[J]. In: ICDE 2004: 301-312.

Research on an Efficient Method for GNN Query Algorithm

HUANG Kai
( Fujian Special Equipment Inspection and Research Institute,Quanzhou Branch Institute,Quanzhou 362000, Fujian, China)

Given a collection of P and Q, then GNN is returned by the query object p in P, p meets to set function all objects in the Q f the minimum distance. There are several methods for GNN. This paper raises the vp-GNN algorithm, which is characterized in that does not use any index case, also can effectively cut to spatial data in the database, reduce the search area and improve the efficiency of GNN query.

Spatial database; Nearest neighbor; Group nearest neighbor

2014-03-25

黄 凯，男，福建省特种设备检验研究院泉州分院，工程师，硕士