基于结构整体损伤指标的钢框架地震易损性研究

徐 强，郑山锁，韩言召，程 洋，田 进

(西安建筑科技大学 土木工程学院，西安 710055)

地震造成的人员伤亡和经济损失与结构的破坏程度直接相关，结构的整体易损性分析与基于性能的抗震设计均需对结构损伤提出一个可以量化的指标，并划分结构不同极限破坏状态。合理的损伤模型应物理意义明晰、应用简便，并能够同时考虑结构的位移首超破坏与累积损伤破坏。

1 结构整体损伤评估指标

1.1 结构损伤模型

结构在地震作用下会产生不同程度的损伤，并随着荷载循环次数的增加不断累积，最终导致结构破坏。目前描述结构损伤有三种方法:一是从材料的角度提出损伤模型，Shen等［1］依据塑性应变与滞回耗能，提出一个适用于钢构件的损伤模型，王连坤等［2］基于钢材各向同性塑性累积损伤本构关系，推导了考虑材料损伤和混合强化本构关系的弹塑性刚度矩阵。丁阳等［3］考虑了钢材的损伤累积效应和应变强化效应，应用塑性应变和能量耗散理论建立了钢材的损伤力学模型。二是建立构件的损伤模型，最典型就是 Park等［4］提出的基于最大反应变形和累积耗能线性组合的双参数地震损伤模型，通过与构件权重系数组合建立结构损伤模型。徐龙河等［5］提出基于应变与比能的双参数钢结构损伤模型。三是直接采用结构宏观性能状态指标，如结构的位移、延性系数、能量耗散等，目前我国规范［6］以及FEMA系列［7］均选用结构层间位移角作为描述结构抗震性能的指标。Bojórquez等［8］依据结构层间位移角作为结构整体损伤指标的不足提出基于能量耗散的损伤指标。

从材料角度建立损伤模型的优点在于理论严谨完整，其缺点计算公式繁琐且数值模拟结果精度难以保证。基于构件的损伤模型的优点在于易通过构件试验验证，且能够描述结构各个构件的损伤程度，其缺点在于计算复杂，不适合灾后快速评估。层间位移角作为结构整体损伤指标的优点在于简单实用，但无法考虑结构的累积损伤对结构抗震性能的影响［9］。

1.2 基于结构整体耗散能量的损伤模型

为解决层间位移角作为结构整体损伤指标无法考虑结构的累积损伤这一问题，Bojórquez等提出基于结构整体能量耗散的结构评估方法，假定结构耗能仅发生在梁端。该方法物理意义明确，定义当结构耗散能量需求大于结构耗散能量能力时，即ID＞1结构倒塌，具体损伤指标［8］:

式中，EDE为结构耗散能量需求，即结构在地震作用下的滞回耗能;ECE为结构耗散能量能力。

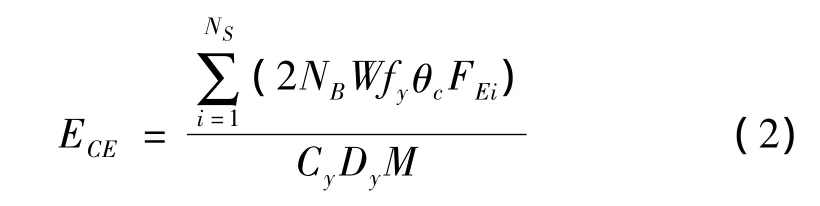
式中，NS和NB为结构楼层数与各层梁的数量;W为截面模量;fy为屈服强度;θc为梁端累积塑性转角;FE为层耗能参与系数;Cy为地震影响系数;Dy为结构屈服位移;M为结构质量。

式中，μ为结构延性系数;h为第i层结构高度;H为结构总高度。当FE＞1时取1。

因FE计算复杂，且需考虑结构延性，通过对不同高度不同延性的钢框架进行非线性动力分析，发现FE沿结构高度的分布趋势近似，均在h/H为0.4附近取得最大值，为简化计算，对计算进行回归分析，取平均值，得到不依赖结构延性的层耗能参与系数FD:

采用FD作为层耗能参与系数的优势在于FD仅取决计算楼层高度，方便灾后对某区域不同结构进行快速评估，而FE需考虑结构延性，较为耗时。9层钢框架与5层钢框架当μ=2、μ=3时FE与FD沿结构高度分布情况如图1(a)与1(b)所示。

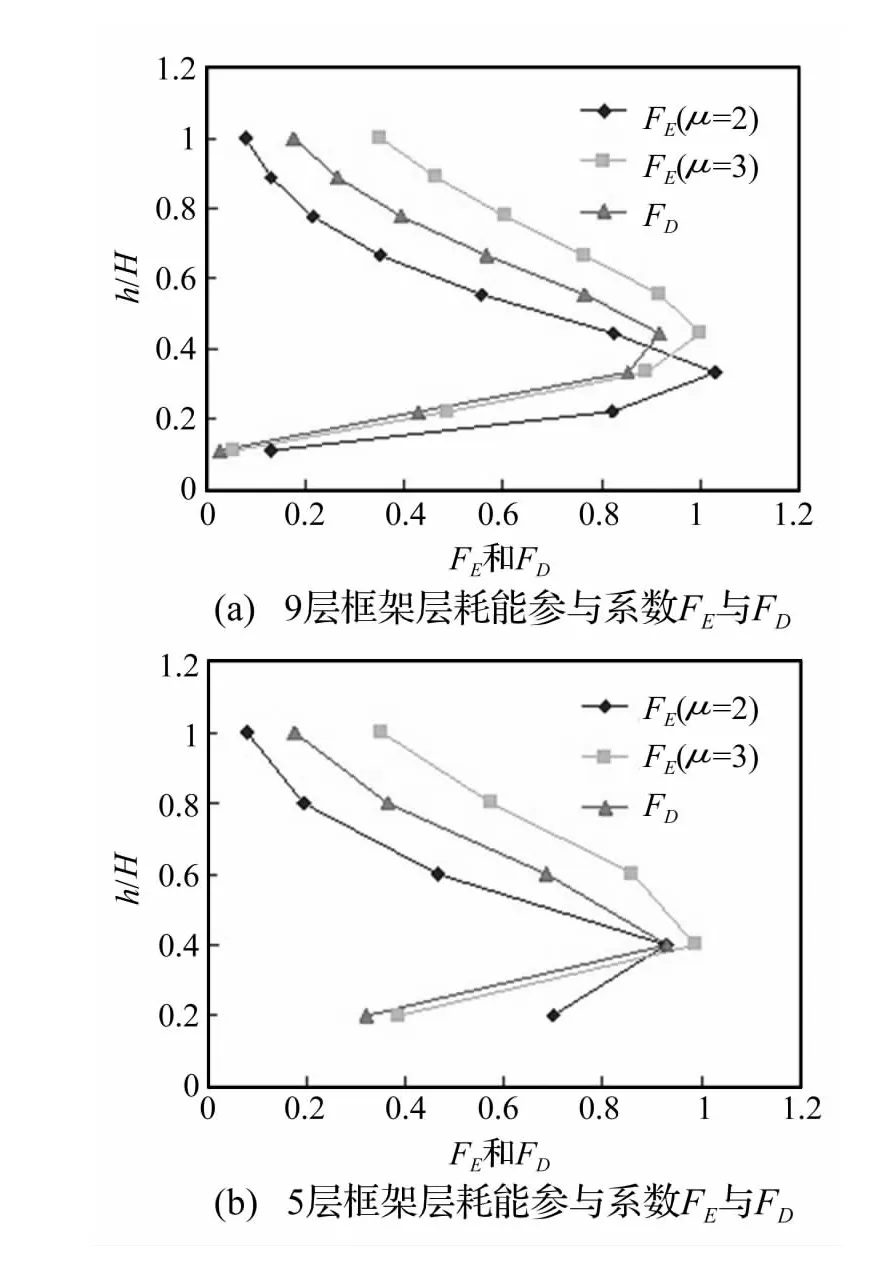
图1 层耗能参与系数FE与FDFig.1 energy participation factorFEandFD

1.3 基于结构层间位移角的损伤模型

为方便对比研究层间位移角与能量耗散指标作为结构整体损伤指标时描述结构损伤程度的差异，将层间位移角标准化:

式中，δD表示结构层间位移角的地震需求，即结构在地震作用下的最大层间位移角;δC表示结构层间位移角的地震能力，即结构在地震作用下保证不倒塌的最大层间位移角，本文综合已有钢框架抗倒塌分析成果取1/25。定义IDδ＞1结构倒塌。

2 结构整体损伤指标对比分析

2.1 计算模型

本文依据《建筑抗震设计规范》(GB50011-2010)及《钢结构设计规范》(GB50017-2003)，采用PKPM软件设计一个6榀3跨的9层梁柱焊接钢框架作为计算模型，如图2所示，跨度均取8 m，层高均为3.6 m，梁采用H型截面，柱采用箱型截面，梁柱截面尺寸见表1，钢材屈服强度为Q345。设计地震分组为第1组，场地类别为Ⅱ类，抗震设防烈度8°，设计基本地震加速度0.20 g。采用ANSYS建立有限元模型，采用应变硬化为3%的弹塑性模型来模拟构件的滞回性能，非线性动力分析时结构阻尼系数取3%，振型考虑前两阶。

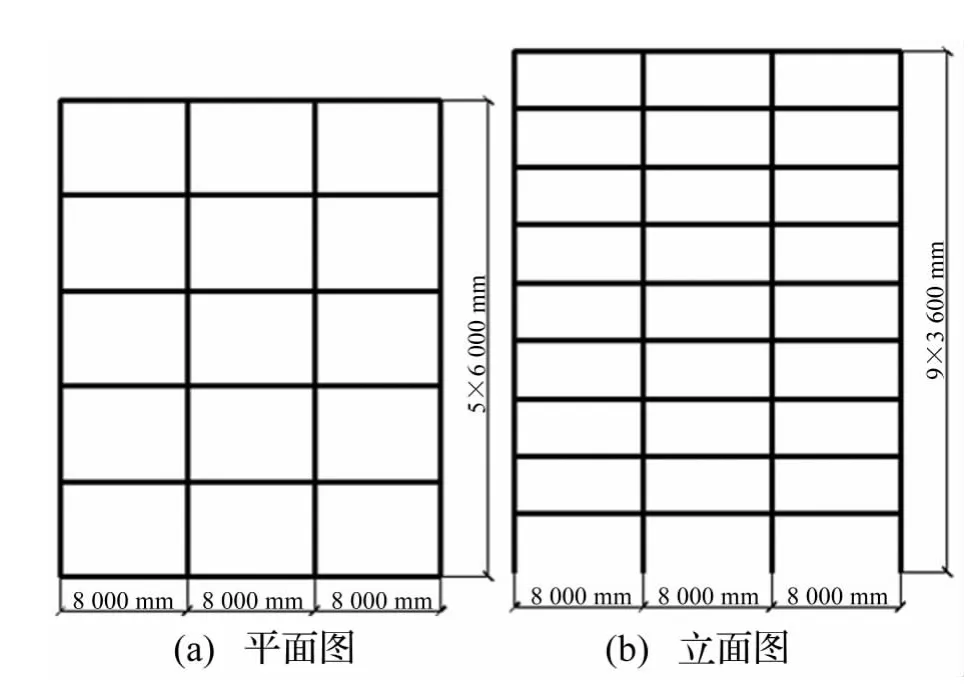
图2 9层钢框架模型Fig.2 9 floors steel frame model

表1 梁柱截面尺寸Tab.1 The section size of column section and beam

2.2 地震波选取

参考ATC-63选波原则［10］，在PEER强震数据库中挑选出20条满足波速范围和震中距要求的地震记录，如表2所示。地震波峰值加速度分别调幅为0.05 g、0.1 g、0.2 g、0.3 g、0.4 g、0.5 g、0.6 g、0.7 g、0.8 g、1 g和1.2 g，作为IDA分析的地震输入参数。

2.3 结构整体损伤模型

结构需求参数D与地震动参数IM之间的关系满足指数关系［11］:

采用层间位移角作为结构整体损伤指标对钢框架结构进行IDA分析，得到结构整体损伤模型的损伤指数与地震动峰值加速度(单位:g)之间的关系:

采用能量耗散作为结构整体损伤指标对钢框架结构进行IDA分析时，考虑到在结构未发生塑性变形前结构损伤指数为零，结构整体损伤模型的损伤指数与地震动峰值加速度(单位:g)之间的关系:

基于层间位移角与能量耗散的结构整体损伤曲线对比如图3所示。

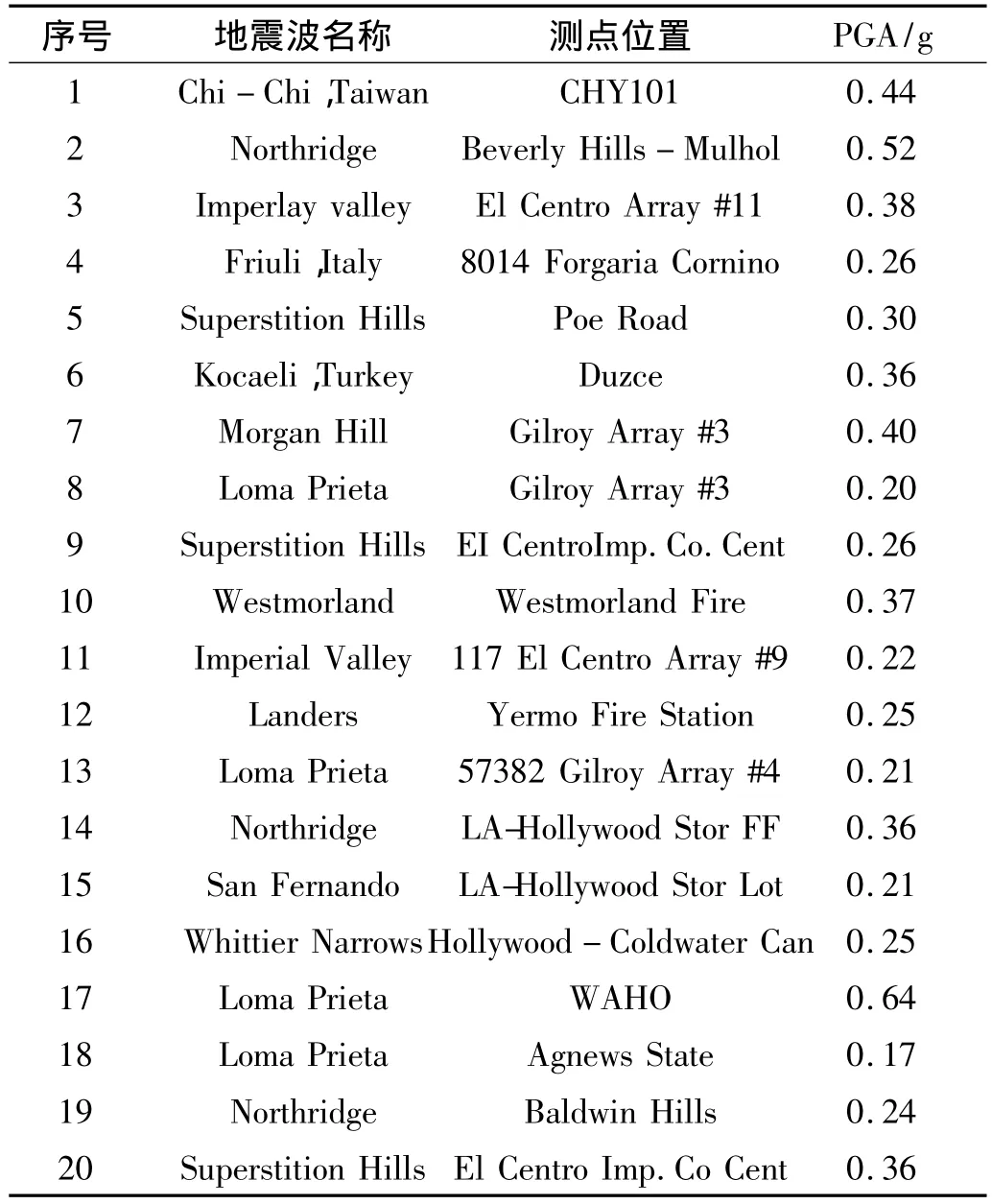
表2 文中选用的地震动记录Tab.2 Selected ground motion records

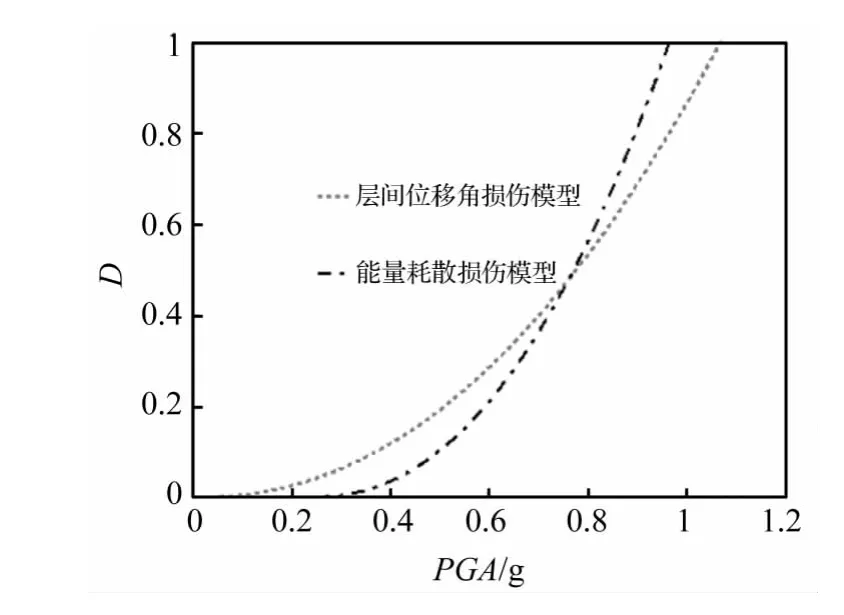
图3 两种结构整体损伤指标的损伤曲线对比Fig.3 Contrast of two global structural damage index

由图3可见，两条结构整体损伤曲线在损伤指数略小于0.5时相交，表明在此时用这两种方法判断的结构损伤程度相同，且对应的结构最大层间位移角是1/45，接近我国抗规规定的罕遇地震作用下结构弹塑性层间位移角1/50的限值。这表明按我国规范设计的结构在达到弹塑性层间位移角1/50的限值时结构耗散能量不到结构自身耗能能力一半，仍有较大的安全储备，能够保证“大震不倒”。

当损伤指标小于0.5时，基于能量法的损伤曲线低于基于层间位移角的损伤曲线，表明以层间位移角为损伤指标判断结构损伤的程度高于以能量耗散为损伤指标判断结构损伤的程度，且当PGA小于0.231 5 g时，以能量耗散为损伤指标判断结构损伤值为零，说明此时结构处于弹性状态，未产生塑性耗能。

当损伤指标大于0.5时，基于能量法的损伤曲线高于基于层间位移角的损伤曲线，表明以层间位移角为损伤指标判断结构损伤的程度偏不安全，特别当以能量耗散为损伤指标判断结构损伤值为1时，说明结构耗散地震能量需求与结构耗能能力相等，此时结构已经破坏，而此时以层间位移角为损伤指标判断结构损伤值仍小于1。

3 结构整体损伤分析

3.1 建立损伤模型

基于规范设计的钢框架结构在遭遇巨震(超过罕遇地震的地震)时在未达到结构极限层间位移角变形(1/25)前就可能因累积塑性耗能需求大于结构耗散能量能力而发生倒塌破坏，可见单一以层间位移角作为结构整体损伤指标会因无法考虑结构累积损伤而过高估计结构抵御巨震的能力。同时，单一以能量耗散作为结构整体损伤指标的缺点在于:①以能量耗散为损伤指标计算得到的是整体结构耗散地震能量需求与结构耗能能力之间的关系，无法判断某一楼层的损伤程度;②无法判别结构失效模式，当地震作用下结构某次位移过大而累计塑性耗能较小时可能发生结构极限层间位移角大于1/25，但以能量耗散为损伤指标判断结构损伤值小于1的情况;③当结构未发生塑性变形时，基于能量法的损伤指标为0，即不能对结构进行弹性分析，无法指导设计;④当结构接近倒塌时，框架柱不可避免会产生塑性耗能，因此仅考虑梁端耗能会低估结构耗能能力。基于此，本文提出基于层间位移角与能量耗散双参数的结构整体损伤模型:

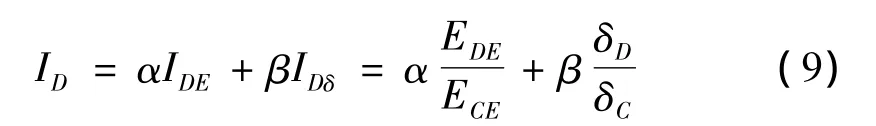
式中，IDE和IDδ分别表示基于能量耗散和层间位移角的结构整体损伤指标，α和β为权重组合系数，且α+β=1。本文取 α =0.3、β =0.7。

3.2 结构损伤模型分析

该模型的优点在于既能够考虑结构累计损伤，又可以考虑结构某次位移过大而累计塑性耗能较小的情况，且能够描述在结构弹性阶段与弹塑性阶段的损伤程度。

将式(7)与式(8)带入式(9)，得到本文结构整体损伤模型的损伤指数与地震动峰值加速度(单位:g)之间的关系:

采用层间位移角、能量耗散以及本文结构整体损伤指标的结构损伤曲线对比如图4所示。

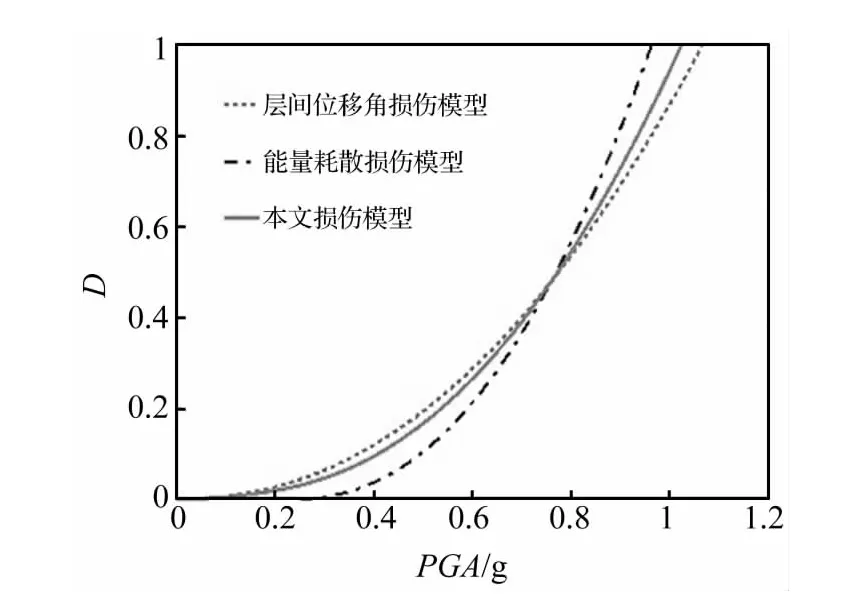
图4 三种结构整体损伤指标的损伤曲线对比Fig.4 Contrast of three global structure damage index

3.3 极限状态定义

结构损伤程度可分为:无损、轻微损伤、中度损伤、重度损伤以及倒塌五个等级，本文结合我国《抗规》规定的多遇地震作用下的弹性层间位移角限值(1/250)与罕遇地震作用下弹塑性层间位移角限值(1/50)，以及已有结构抗倒塌分析成果，给出以层间位移角作为结构整体损伤指标时钢框架4种极限状态及相应的层间位移角限值与损伤指数，见表3。基于能量耗散及本文确定的损伤指数与基于层间位移角的损伤指数确定的结构破坏程度与损伤指数范围相同。

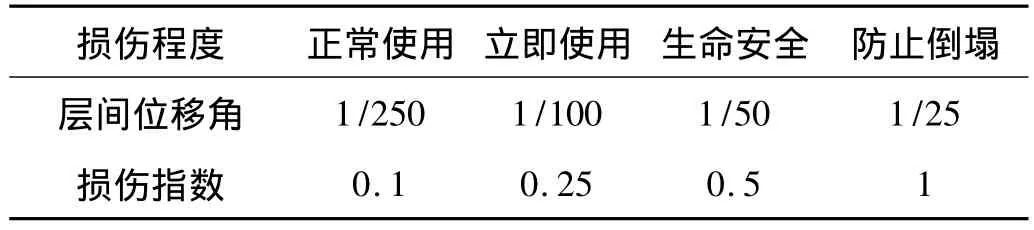
表3 结构破坏极限状态与损伤指标Tab.3 Structural failure limit state and damage index

3.4 基于结构整体损伤指标的易损性分析

结构的易损性分析主要用于评估结构的抗震性能，计算不同强度地震作用下结构反应超过极限状态所定义的结构能力参数的条件概率。假定结构的地震需求D与地震能力C均服从对数正态分布［12］，结构特定阶段的失效概率Pf表示为:

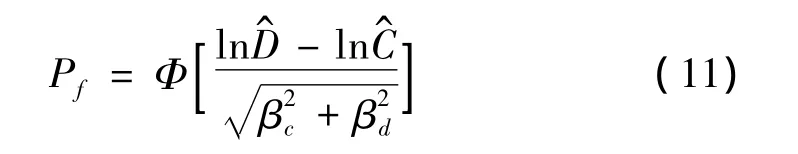
式中:和βd分别为结构需求参数的均值和对数标准差和βc分别为结构能力参数的均值和对数标准差。βd与βc根据结构易损性曲线参数高标准耐震设计规范HAZUS99［13］取值，当易损性曲线以PGA为自变量时取 0.5。

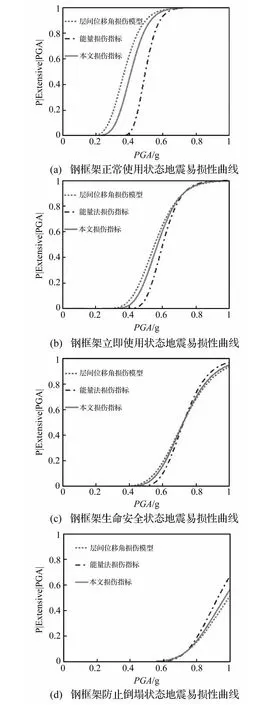
图5 4种极限破坏状态的钢框架易损性曲线Fig.5 Vulnerability curve under four kinds of ultimate state

将式(7)、(8)与式(10)代入式(11)，得到三种结构整体损伤指标在4种不同性态水平下的结构地震易损性曲线图5所示，横坐标为地震动峰值加速度，纵坐标为结构破坏的超越概率。

由层间位移角、能量耗散与本文建立的结构整体损伤模型的结构损伤曲线与易损性曲线可见，基于本文提出的双参数结构整体损伤指标能够更加合理的评定结构在地震作用下的损伤程度，且能够考虑整体结构的首超破坏与累计损伤，因此该损伤模型是合理的、合适的。

4 结论

本文考虑不同结构整体损伤指标对评判结构损伤程度的影响，主要结论如下:

(1)以9层梁柱焊接钢框架为例，选取20条满足场地条件的地震波，对结构进行IDA分析，对比分别以层间位移角和能量耗散作为结构整体损伤指标时结构损伤程度，发现仅以层间位移角作为结构整体损伤指标会高估结构抗倒塌能力。

(2)单一以层间位移角作为结构整体损伤指标无法考虑结构在地震作用下的累积损伤，单一以能量耗散作为结构整体损伤指标无法考虑结构在地震作用下的首超破坏且不能对结构在弹性阶段作出损伤评定。

(3)基于层间位移角和能量耗散的双参数线性组合的结构整体损伤模型能够有效的评估结构的损伤程度，且考虑整体结构的首超破坏与累计损伤，可以认为是一种合理的整体结构评估模型。

［1］ Shen Z Y，Dong B.An experiment-based cumulative damage mechanics model of steel under cyclic loading［J］.Advances in Structural Engineering，1997，1(1):39-46.

［2］王连坤，郝际平，张俊峰，等.考虑各向同性塑性损伤的钢结构塑性区分析方法［J］.西安交通大学学报，2008，42(7):885-890.

WANG Lian-kun，HAO Ji-ping，ZHANG Jun-feng，et al.Plastic-zone method of steel structure considering isotropic plastic damage ［J］.Journal of Xi'an Jiaotong University，2008，42(7):885-890.

［3］丁阳，郭峰，李忠献.地震作用下空间网架结构考虑损伤累积效应的弹塑性分析［J］.工程力学，2005，22(1):54-58.

DING Yang， GUO Feng， LI Zhong-xian. Elasto-plastic analysisofspatialtrussesunderearthquake excitations considering damage accumulation effect［J］.Engineering Mechanics，2005，22(1):54-58.

［4］ Park Y J，Ang A.Mechanistic seismic damage model forreinforced concrete［J］.Journal of Structural Engineering，1985，111(4):722-739.

［5］徐龙河，杨冬玲，李忠献.基于应变和比能双控的钢结构损伤模型［J］.振动与冲击，2011，30(7):218-222

XU Long-he，YANG Dong-ling，LI Zhong-xian.Strain and energy ratio-based damage model of a steel structure［J］.Journal of Vibration and Shock，2011，30(7):218-222.

［6］GB50011-2010.建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［7］FEMA 356.Prestandard and commentary for the seismic rehabilitation of builings［S］.Washington D C，2000.

［8］ Bojórquez E， Reyes-Salazar A，Terán-Gilmore A，et al.Energy-based damage index for steel structures［J］.Steel and Composite Structures，2010，10(4):343-360.

［9］ Hancock J，Bommer J J.A state-of-knowledge review of the influence of strong-motion duration on structural damage［J］.Earthquake Spectra，2006 ，22(3):827-845.

［10］ ATC-63. Quantification ofbuildingseismicperformance factors［R］.ATC-63 Project Report(90%Draft)，FEMA P695/April 2008.

［11］ Cornell C A，Jalayer F，Hamburger R O，et al.Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines［J］.Struct.Eng.，2002，128(4):526-533.

［12］Sucuogˇlu H，Yücemen S，Gezer A，et al.Statistical evaluation of the damage potential of earthquake ground motions［J］.Structural Safety，1998，20(4):357-378.

［13］ HAZUS99，User's manual［S］.Washington D C:Federal Emergency Management Agency，l999.