基于MATLAB的发动机万有特性曲面拟合

（同济大学汽车学院，上海200092）

基于MATLAB的发动机万有特性曲面拟合

黄风清

（同济大学汽车学院，上海200092）

基于软件建模的理论研究方法在整车开发中占据了越来越重要的地位。发动机作为整车中最为重要的一个零部件，发动机的万有特性如何通过数学模型更准确地表达出来，对整车模型的计算精度有非常重要的意义。通过建立不同的数学模型，依靠MATLAB的曲面拟合计算功能，找到更为精确的发动机万有特性曲面拟合方程。

发动机数学模型MATLAB

1 前言

基于软件建模的理论研究方法在整车设计开发中发挥了越来越重要的作用。通过建立整车的模型，形成虚拟样机，可以更好地辅助设计师选择更优的设计参数、较准确地评估整车性能以及预测整车的各项参数。整车油耗的模拟计算往往是整个模型中的重点与难点，因为影响整车油耗因素有：发动机本体的性能、传动效率、外部阻力、使用工况、人为操作习惯等。针对如何提升模型对整车油耗计算的准确性，本文主要研究如何提高对发动机万有特性拟合的精度，以达到提高模拟计算精度的目的。

2 研究对象

本文的研究对象为上柴动力SC9DK220G3型发动机。该款发动机的供油系统为高压共轨，排放限值达到非道路用第Ⅲ阶段的要求，是上柴公司为非道路用第Ⅲ阶段排放打造的升级动力，具有油耗低、加速性好等优点。其主要参数如表1所示。

表1 柴油机基本参数

3 发动机数学模型的建立

发动机的万有特性曲线可以较全面地表示发动机的性能。通常以发动机的转速为横坐标，发动机的扭矩为纵坐标，在图上可以表示出等油耗率曲线、等小时耗油量曲线、等功率曲线、等过量空气系数曲线、冒烟极限等。

3.1 基于多项式的数学模型

根据发动机负荷特性定义，固定发动机转速，对表达式进行降维处理[1]，对其进行一元曲线拟合，其燃油消耗率be的表达式为：

式（1）表示为发动机在转速ni下的负荷特性，若固定j，则式（1）中的Aij均为转速n的函数，其表达式可写为：

将式（2）代入式（1），可以得到通用的计算公式

其中i=(1,2,3…K)，j=(1,2,3…S)

根据式（3）及图1燃油消耗率be与转速n和功率P的曲线关系，结合计算复杂程度，分别选取K=S=3进行拟合计算。对多项式的拟合就是求解多项式系数的过程，实际上就是求解多项式系数Cij的过程（下文称“方法1”）。

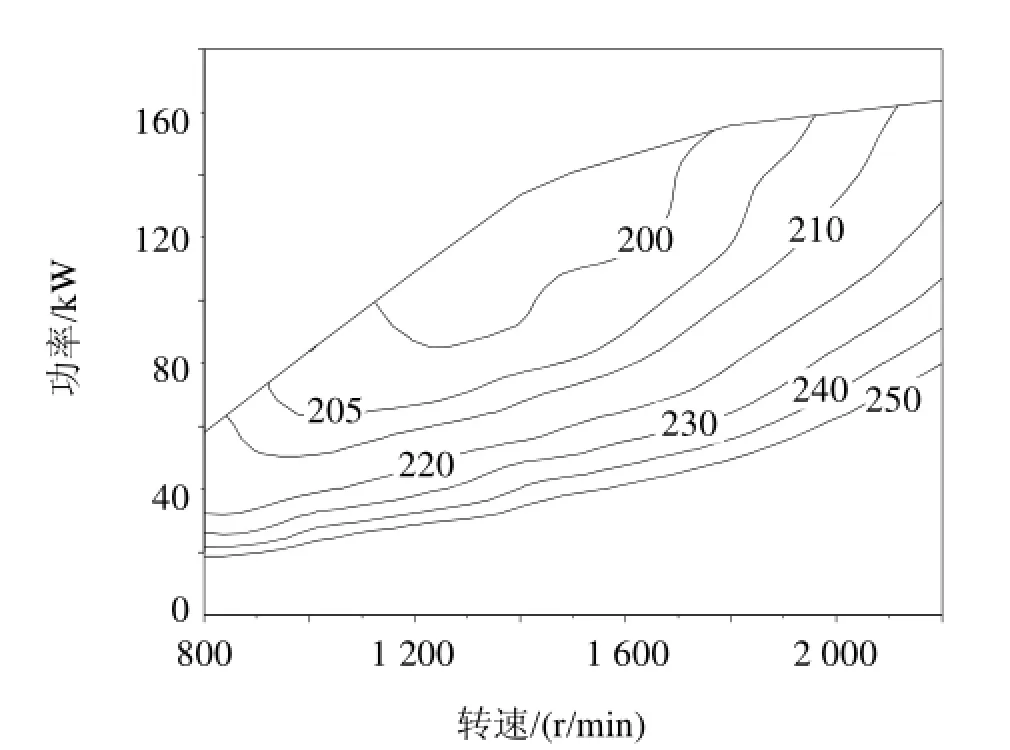
图1 发动机等油耗率曲线

根据已有的实测数据，基于MATLAB的拟合计算，得到多项式（3）各项系数，见表2。

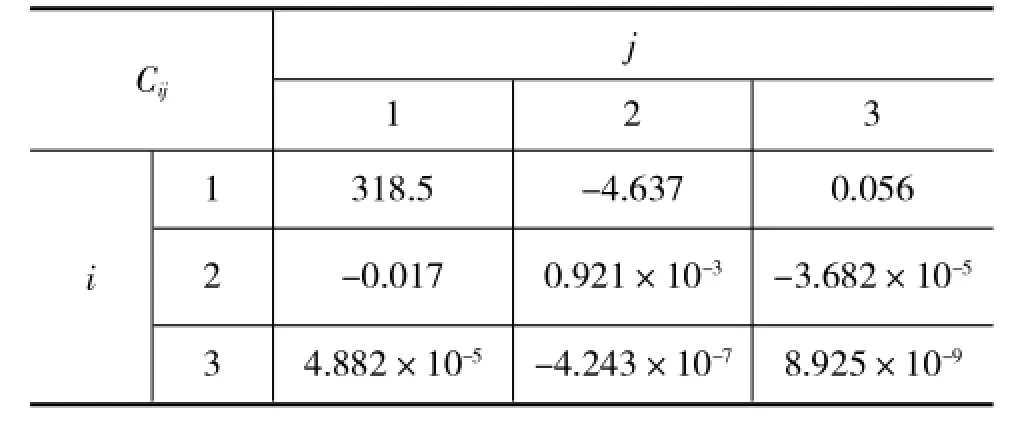
表2 拟合多项式系数Cij

3.2 基于幂函数的数学模型

为了提高模型的准确度，在建立基于幂函数的数学模型时，发动机的万有特性曲线以等小时油耗量的形式来表达，如图2所示。其主要表现为发动机的小时油耗B与转速n和扭矩T的关系，类似幂函数[2]，其函数表达式如下(以下称“方法2”)：

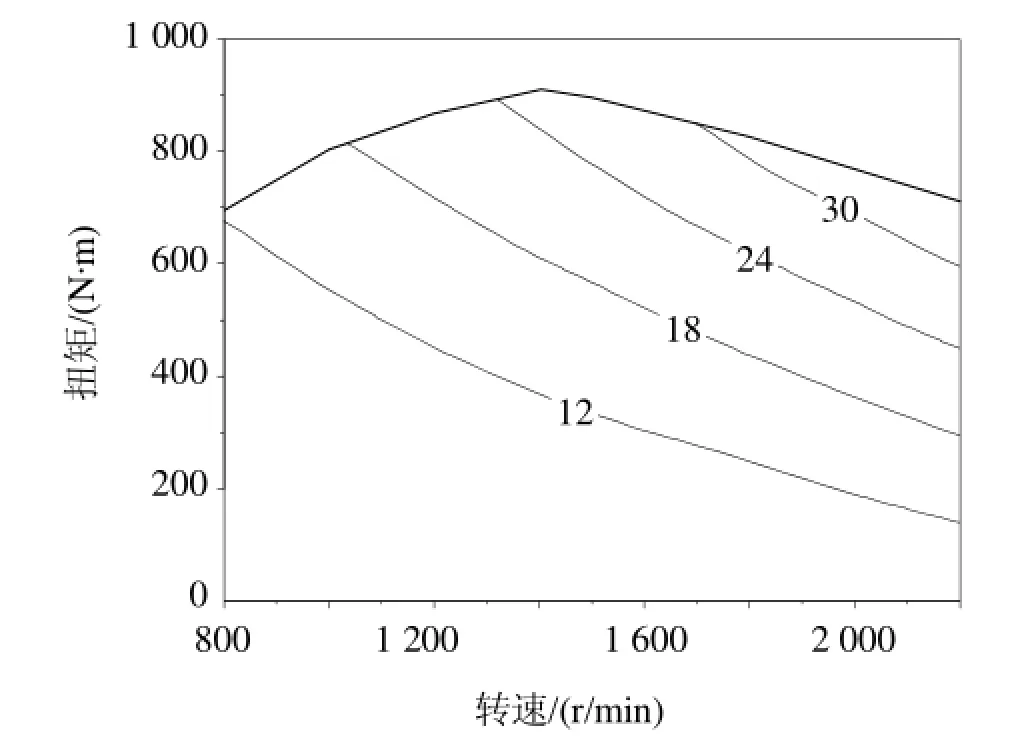
图2 发动机等小时耗油曲线

对（4）进行线性化处理，分别对两边取对数，即由非线性回归问题转化为线性回归问题：

分别令y=lnB，x1=lnn，x2=lnT，相对应地，式（5）可以表示成

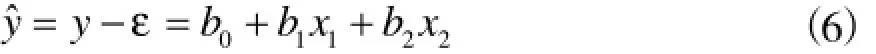
其中，yˆ为模型估算值，b0、b1、b2为回归系数，y为实测值，ε为残差。

式（6）的回归模型为：

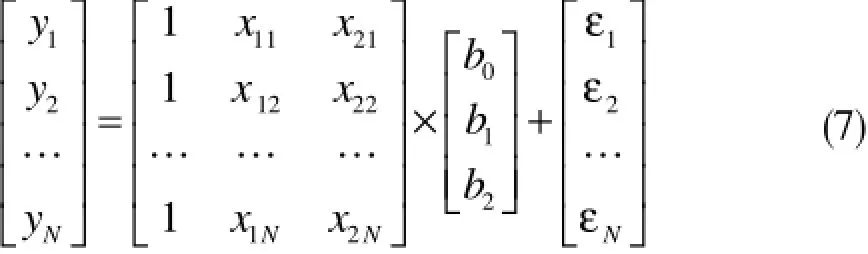
基于MATLAB的拟合结果，分别得到：

b0=-9.494

b1=1.077

b2=0.719

根据上文假设的对应关系，可得：

a0=e-9.494

a1=b1=1.077

a2=b2=0.719

分别代入式（4），其函数表达式为：

根据式（8）对发动机的小时耗油量进行估算，在发动机低负荷，尤其是低速低负荷区域存在较大误差，如果以此进行模拟计算，必将影响模型的计算精度。所以在方法2的基础上，对函数的自变量发动机转速n和发动机扭矩T的定义域进行划分，其函数表达式同式（4）（以下称“方法3”），分别获得几组回归系数，如表3所示。

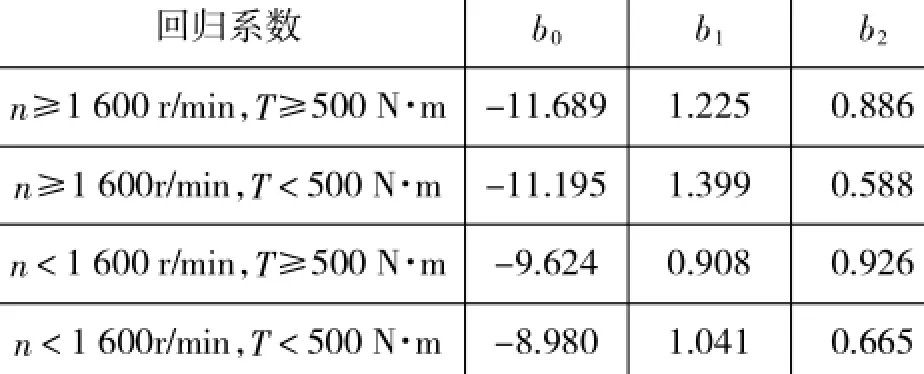
表3 分段函数的回归系数及自变量定义域

根据表3回归系数，发动机的小时耗油量B与发动机转速n和发动机扭矩T的表达式可写为：

4 模型分析与验证

4.1 基于MATLAB计算参数对模型进行分析

根据MATLAB计算出的统计检验结果，分别对方法1、方法2、方法3进行比较，3种方法对应的统计检验相关的参数：相关系数R2、检验回归方程显著性的F值、残差的方差如表4所示。

表4 模型的统计检验结果

从表4数据可知，3种方法相关系数R2均大于0.8，可以认为3种方法均高度相关；基于F值的大小，方法2和方法3拟合的显著性比方法1更显著；从残差的方差来看，方法1的误差明显大于方法2和方法3。所以根据表4几项检验模型的重要参数的比较可知，方法2和方法3明显优于目前较常用的方法1。对发动机负荷较大的工作区域的拟合，方法3优于方法2；在进行整车模拟计算时，若发动机常工作于高速高负荷区域，方法3的精度优于方法2。

4.2 模型计算值与实际值的对比验证

通过模型的计算与实测数据进行对比，3种方法的相对误差如表5所示。方法3的相对误差最小，均小于2%；方法2在高速高负荷工况有较高的精度，在低速低负荷的工况下，相对误差较大；方法1整体相对误差较大，对模拟计算的准确性会产生较大的影响。

针对例如城市公交的匹配计算，由于其常处于低速低负荷工况，必须用方法3才能确保其模拟计算的精度，而针对大部分工程机械用机型，由于其常处于高速高负荷的工况，为了简化计算量，可以采用方法2进行整车模拟计算。

5 总结

通过建立准确的数学模型，可以大大降低整车开发中的人力及物力成本，简化整车性能验证时间和试验强度，对整车企业及发动机配套企业均具有较重要的意义。

1陈朝阳，赵正彩，余中桂等．汽车发动机万有特性曲面拟合的一种新方法[J]．安徽工学院学报，1994，13（2）：35-40．

2钱俊，黄风清，姜锋．柴油机不同功率模式对装载机性能影响的仿真研究[J]．柴油机设计与制造，2014（2）：16-20，53．

Fitting of Engine Performance Map Based on MATLAB

Huang Fengqing
（School of Automotive Engineering,Tongji University,Shanghai 200092,China）

A research method of building mathematical models based on professional software is playing a more and more important role in vehicle development project.How to more accurately describe with mathematical models the performance map of engine that is one of the most important parts of vehicle is of great significance to the precision of vehicle calculation.A more accurate fitting equation for engine performance map is developed by building several different models and adopting the MATLAB fitting calculation function.

engine,mathematical model,MATLAB

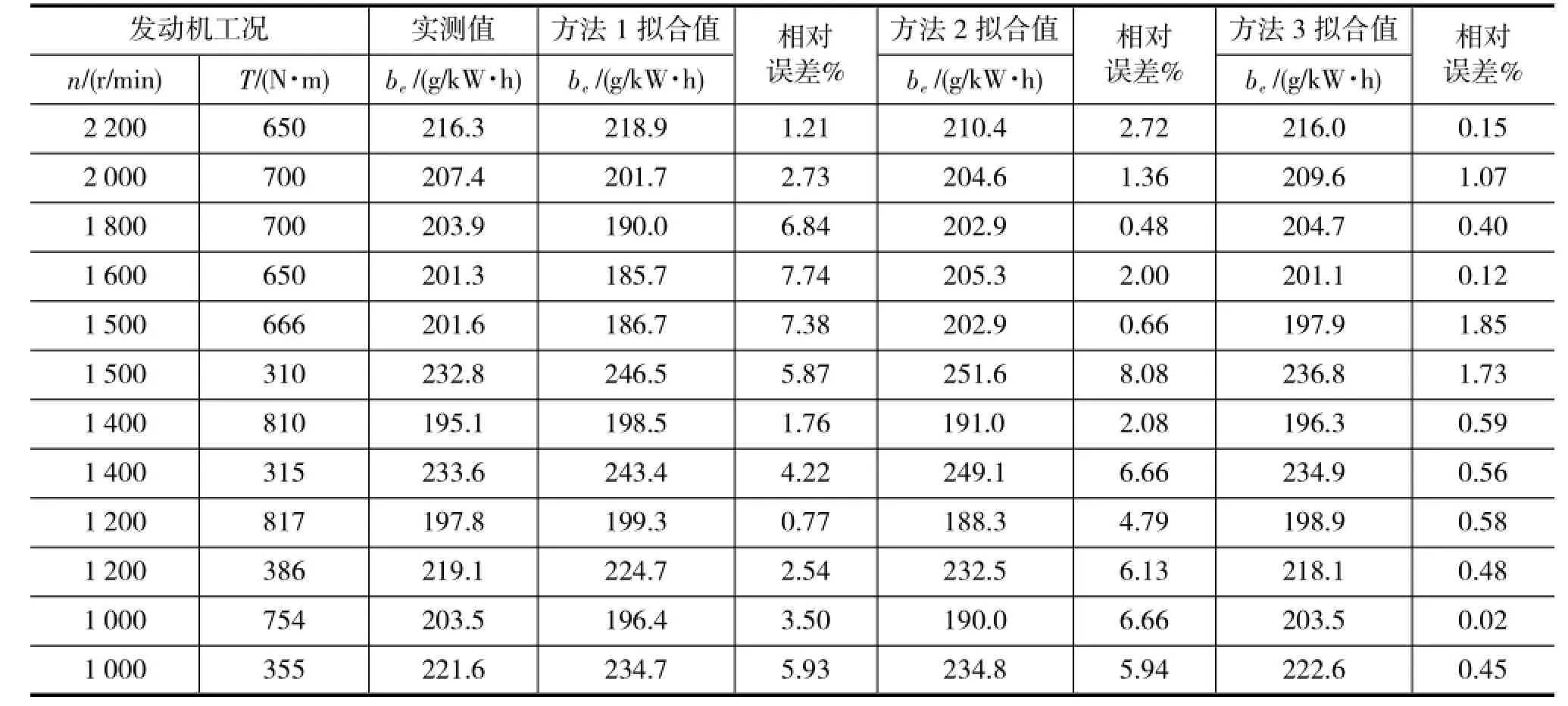
表5 3种方法的相对误差

来稿日期：2014-06-30

黄风清（1982-），男，工程师，主要研究方向为整车与发动机匹配技术。

10.3969/j.issn.1671-0614.2014.03.003