建构主义下数学实验课的教学设计与实施策略

岑冠军， 蔡贤资

(华南农业大学 理学院，广东 广州 510642)

0 引 言

近年来，国内许多学者提倡将数学实验的思维和方法融入到高等数学课的教学中[1-2]，数学实验作为一门新实践课程被国内众多高等学府引入到大学课程体系中。许多学者从不同的角度提出了大学数学实验课的多种教学模式[3-6]，但是对这些教学模式如何在课堂中具体实施却缺乏研究。在实际教学中，数学实验课学时短，教学班人数多[7-8]，课堂教学该如何开展、组织、管理和监控？教师如何看待自己的角色？一些数学实验课涉及到案例的专业背景知识、数学理论和计算机编程知识，教师如何引领学生在这些知识间穿梭并完成实验任务？这些都是数学实验课教师面临的切实问题。数学实验课涉及到多学科的交叉，其课堂教学与传统课堂教学存在明显的差异[9]，需要现代教育理论的指导。本文从建构主义学习理论出发，并结合笔者的教学实践，以综合性数学实验为例，探究大学数学实验课的课堂教学设计及实施策略，为广大数学实验课教师改进课堂教学提供有益借鉴，以期提高数学实验课的教学水平。

1 建构主义学习理论下数学实验课的教学设计

建构主义学习理论认为知识不是通过传授得到，而是学习者在一定的情境即社会文化背景下，借助他人(包括教师和学习伙伴)的帮助，利用必要的学习资料，通过意义建构而获得的[10]。著名的数学教育家波利亚曾指出：“数学有两个侧面，一方面，它是欧几里得式的严谨科学，从这个方面看，数学像是一门系统的演绎科学；另一方面，创造过程中的数学，看起来却像一门实验性的归纳科学”，数学既是一门演绎科学，也是一门实验性的科学。数学理论的发现创造来源于人类的实践活动，数学实验课就是让学习者进行数学实践活动的课程，学习者从活动的过程中获取解决问题的有效途径与方法，理解并掌握知识间的内在联系与规律，并获取积极的情感体验，数学实验应该在建构主义环境下进行[11]。数学实验教学的本质是将实际数学活动引入到教学过程中，是对实际数学活动的模拟与再现[12]。因此，建构主义理论下数学实验课教学设计的核心就是为学生创设数学实践活动的情景，让学生在教师创设的数学实践活动情景中进行实验探索、模型验证和结果解释，最终给出实际问题的答案。学生是数学实践活动的主体，教师是其协助者，学生在此实践活动中建构自己应用数学的技能和经验，教师要做的就是让学生充分参与到这一实践活动中并保证活动的顺利进行。

下面以“健康猪肌注给药的一室模型”为教学案例来谈建构主义下大学数学实验课教学的具体设计，该教学案例来源于由张国权等主编的《数学实验》第四章综合实验四[13]。该教学案例具有典型的农科专业特色，其科研实践背景来源于文献“沙拉沙星在猪体内的药动力学研究”[14]。案例的具体内容是探究药物沙拉沙星(Sarafloxacin, 商品名Saraflox)通过肌肉注射到健康猪体内后，该药物在猪体内的吸收与扩散规律。对于本教学案例，其数学实践活动就是用数学语言描述药物在猪体内的吸收和扩散过程，通过数学实验探索药物在猪体内的吸收扩散规律。

建构主义学习理论强调学习的情景性、主动性和社会性，为了给学生创设体验情景，同时营造教师引导、同学间相互交流的自主性学习氛围，笔者将本实验课教学划分为7个环节，如图1，将学生6到7人编为一组，每一组选取一名学生做组长，每个组成员分配一项主要负责任务，如数学建模、模型求解、程序编写、模型解释等等，其他组成员协助。

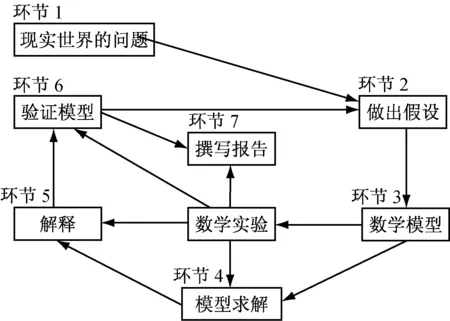
图1 建构主义下数学实验课的教学环节设计

(1) 环节1让学生进入现实世界问题的情景中。笔者给适当地时间让学生阅读并思考该实际问题，各个小组讨论。笔者从两个方面来引导学生：第一，提示学生找出实际问题中的关键词；第二，提示学生可以将自己理解的药物吸收扩散过程用图形来表示。笔者在实践中，询问学生找到的关键词，展示他们所画的吸收扩散过程的图形，将他们找到的关键词写在黑板上，如均匀、吸收、分布、扩散和血药浓度等等，选取其中一组理解较为正确的图形绘在黑板上(见图2)。

图2 药物的吸收扩散过程

(2) 环节2做出假设，让学生进入真实问题的抽象简化情景中。假设是将现实世界问题转化为数学问题的桥梁，在课堂上，多数教师会直接给出假设，忽略了学生这方面能力的培养。在教学中教师应该引导学生根据实际问题做出合理的假设，让学生参与到做假设的过程中，使学生的思维从现实世界逐渐过渡到数学世界中。在本环节，笔者对学生做以下三个方面的引导：①提示学生做假设的目的是为了简化实际的问题，药物在猪体内的吸收扩散是一个极其复杂的生理化学过程，提醒学生我们只是从数量方面来研究这一过程，如何假设能简化这一过程；②既然我们是从数量方面研究药物的吸收扩散过程，提示学生找出这一过程所涉及的变量或者常量；③明确了吸收扩散过程以及该过程涉及到变量之后，引导学生考虑变量之间的关系，对一些变量之间的关系也要做出假设。

在本环节的教学实践中，有的学生提议将猪视为一只箱子，只要关注药物的流进流出，而不管箱子里面发生了什么变化，尽管“箱子”与畜牧兽医学中的术语“房室”相差甚远，但这是一个积极的信号，笔者顺势将图2中的猪用箱子来代替，见图3。根据图3，学生们很快找到一些变量，如时间t、初始的血药浓度C0，箱子A的血药浓度Ca(t)、箱子B的血药浓度C(t)、箱子A血药浓度的变化速率Va(t)、箱子B血药浓度的变化速率V(t)，药物的吸收速率Vs(t)和药物的扩散速率Vd(t)，并发现药物的吸收速率和扩散速率分别与箱子A和箱子B的血药浓度存在一定的关系，需要进一步假设，一些学生提议将这些关系假设成正比关系，可能源于在理论课中正比关系是他们接触最多的一类假设关系。

图3 简化的药物吸收扩散过程

(3) 环节3是建立数学模型，在环节2，学生做出了假设，并找到了相关的变量，笔者将这些变量标注在图3相应位置上，得到图4。笔者从两个方面来引导学生：第一，提示学生选择一种数学理论来描述图4所示的吸收扩散过程；第二，建立数学模型就是要挖掘图4所示的各变量之间的关系，尝试写出这些关系的数学表达式。

图4 量化的药物吸收扩散过程

笔者在实践中看到学生们会写出很多关系式，如：

Va(t)=-Vs(t),V(t)=Vs(t)-Vd(t)

Vs(t)=kaCa(t)，Vd(t)=kC(t)

这说明学生正在建构现实世界问题的数量关系。

(4) 环节4开始引入数学实验，让学生进入到真实问题的数学实验探索情景中。具体设计如下：第一，让学生解微分方程组，获得吸收过程和扩散过程中药物随时间变化的函数后，让学生试述其规律；第二，让学生运用计算机及数学软件Matlab来解上述微分方程组；第三，教师在黑板上给出模型中参数的值，让学生用数学软件Matlab模拟计算在不同的时刻，吸收过程和扩散过程药物浓度的值。

(5) 环节5解释，在获得了模型的解之后，让学生阐述药物在猪体内的吸收扩散究竟是怎样的规律。本环节具体实施如下：第一，运用插值法，让学生用Matlab画出猪体内药物随时间变化的曲线；第二，让学生分组讨论曲线所反映的规律，并用文字来描述。

(6) 环节6模型验证，笔者给出血药数据随时间变化的真实观察数据。并做两个方面的引导：第一，通过数学实验，直观判断他们所建立的模型与真实数据是否吻合，也就是观察真实数据连线图的形状与他们所建立模型的曲线形状是否一致。第二，通过量化指标来评价模型的拟合优度，笔者给出Matlab非线性拟合的命令nlinfit和RMSE的函数，让学生通过计算模型拟合的RMSE来评价模型。

2 建构主义下的大学数学实验教学实施策略

建构主义学习理论下的数学实验课是要让学生自己进行数学实践活动，激发学生自主探索的精神，如何保证学生的数学实践活动顺利进行是课堂教学的焦点。笔者在实践中总结了以下四点实施策略。

2.1 以数学实验为中心，遵循数学建模的脉络主线

当学生成为数学实践的主体时，学生的自由发挥空间较大，容易让课堂教学不可控，为了让学生的数学实践活动向前推进，笔者构建了以数学实验为中心、数学建模为脉络主线的数学实验课堂教学过程(见图1)。在具体实施时，各教学环节紧密围绕数学实验展开，目标明确内容清晰，从环节4～7均开展了数学实验，在环节1～3中通过找关键词、画图和找变量发现问题提出假设，这其实也是一种数学实验；与此同时各环节又按照数学建模的步骤向前推进，环节1～7是一个完整的数学建模过程，包含了发现问题、提出假设、解决问题和结果解释，保证了实验课程的顺利进行。

2.2 适度地引导和干预，让学生在探究中突破难点

数学实验尤其是综合性数学实验往往是面向非数学专业类学生开设的课程，大部分学生没有上过数学建模课，因此在上数学实验课时，学生普遍感觉比较困难。如果学生在一些环节遇到障碍不能及时排除，学生的数学实践活动将不能进行下去。笔者在具体实施时，将学生分成若干小组，跟踪各实验环节在各小组的进展情况，以提示的方式，巧妙地适度地进行引导和干预，并配合提问，帮助学生解决各实验环节中的难点，让学生的数学实践活动的顺利进行。在环节1中笔者提示学生找出实验案例中的关键词，以便学生抓住实际问题的本质。在环节2中让学生画出药物的吸收扩散过程图和找出变量，引导学生做假设。在环节3中让学生写出环节2中他们找出的变量之间关系表达式，帮助学生建立模型。环节4、5和6笔者引导学生解方程组、绘制模拟曲线和真实数据连线图，最终进行非线性拟合，一步一步帮助学生解释模型和评估模型。学生遇到问题时也可在小组内讨论找出解决办法，这样学生就像“研究者”一样，自己发现和探索问题，通过自己的活动，参与建构数学的过程中，提高了学生的参与、探究、创造能力，顺应了当代高等教育的发展趋势[15]。

2.3 避免让学生陷入专业术语和计算推理细节的困境中，专注于实际问题的解答

数学实验尤其综合性数学实验的案例往往具有很强的专业背景，一些案例涉及到的专业术语较多，学生难以理解产生畏难情绪，使得后续数学实践活动进行受阻。本案例就涉及到畜牧兽医学的背景知识，比如药物动力学、房室、吸收室、分布室、吸收速率常数、消除速率常数等诸多术语。笔者在具体实施时，将其中的一些术语转换成学生容易理解和接受的语言，比如在环节2，笔者采用学生提出的“箱子”来代替畜牧兽医学中的术语“房室”，药物从箱子A流入箱子B是药物的吸收，药物从箱子B流出是药物的扩散。采用学生提出的将药物的吸收速率与箱子A的血药浓度假设成正比关系，将药物的扩散速率与箱子B的血药浓度假设成正比关系，避免了引入吸收速率常数、消除速率常数等概念。课堂焦点始终放在数学建模和数学实验上。

在实际教学中，当模型建立后，一些教师习惯于在黑板上进行大幅演绎推理模型求解，讲解非线性拟合的计算细节，笔者认为，数学实验课不同于数学理论课，重在数学应用能力和动手能力的培养，让学生学会运用数学软件解数学问题，是数学实验课的目的之一，尤其是对于非数学专业的学生，数学软件就是让他们从繁琐的计算推理细节中解放出来，更加专注于实际问题的解答。

2.4 分组进行数学实践活动，便于课堂教学的组织和管理

建构主义下数学实验课是教学是让学生自主进行数学实践活动，自主探索过程中学生会遇到许多问题需要教师的帮助，教师会忙于回答个别学生的提问，很难对整个课堂教学进行有效的组织和管理，甚至一些学生游离于课程氛围之外，极大地降低了数学实验课的教学效果。同时建构主义鼓励学习者在与他人的交流协作中完成学习任务，因此上数学实验课时，教师要注意营造交流协作的课堂氛围。对学生进行编组，一方面教师通过监控各个教学环节在各小组的进行情况，可以实时了解学生实验任务的完成进度，对各小组的实验活动进行区别指导和干预；另一方面每个学生都处在一个团队中，形成了良好的交流协作的学习环境，学生在团队里被赋予任务和角色，其主观能动性被极大地调动，提高了学生参与数学实践活动的效率。

3 实验教学效果反馈

笔者在实验课后对学生进行了问卷调查，本次实验课2个班共65人，调查项目及结果整理成表1。

调查结果表明，在环节1大部分同学能找出实验案例中的关键词，画出自己理解的药物吸收扩散流程图，这说明通过教师的引导大部分同学进入到实际问题的情景中；在环节2多数同学能将复杂的实际问题简化，找出实际问题中隐藏的变量，做出自己的假设，发挥了自己的抽象思维；在环节3绝大部分同学能找出一个或一组变量关系表达式，多数同学建立了自己的药物吸收扩散模型，这说明大部分同学能将实际问题转化或者部分转化成数学问题；在环节4和环节5绝大部分同学能用Matlab解微分方程组并用Matlab绘制了猪体内药物浓度随时间变化的曲线，这说明大部分同学自主进行了药物吸收扩散规律的实验探索；在环节6多数同学完成了模型的模拟和评估，完成了数学实验任务。调查结果表明绝大部分同学在本次实验课中充分参与到实验的各个环节中，通过本次实验基本掌握了应用数学理论和软件解决实际问题的过程，实验课教学效果良好。

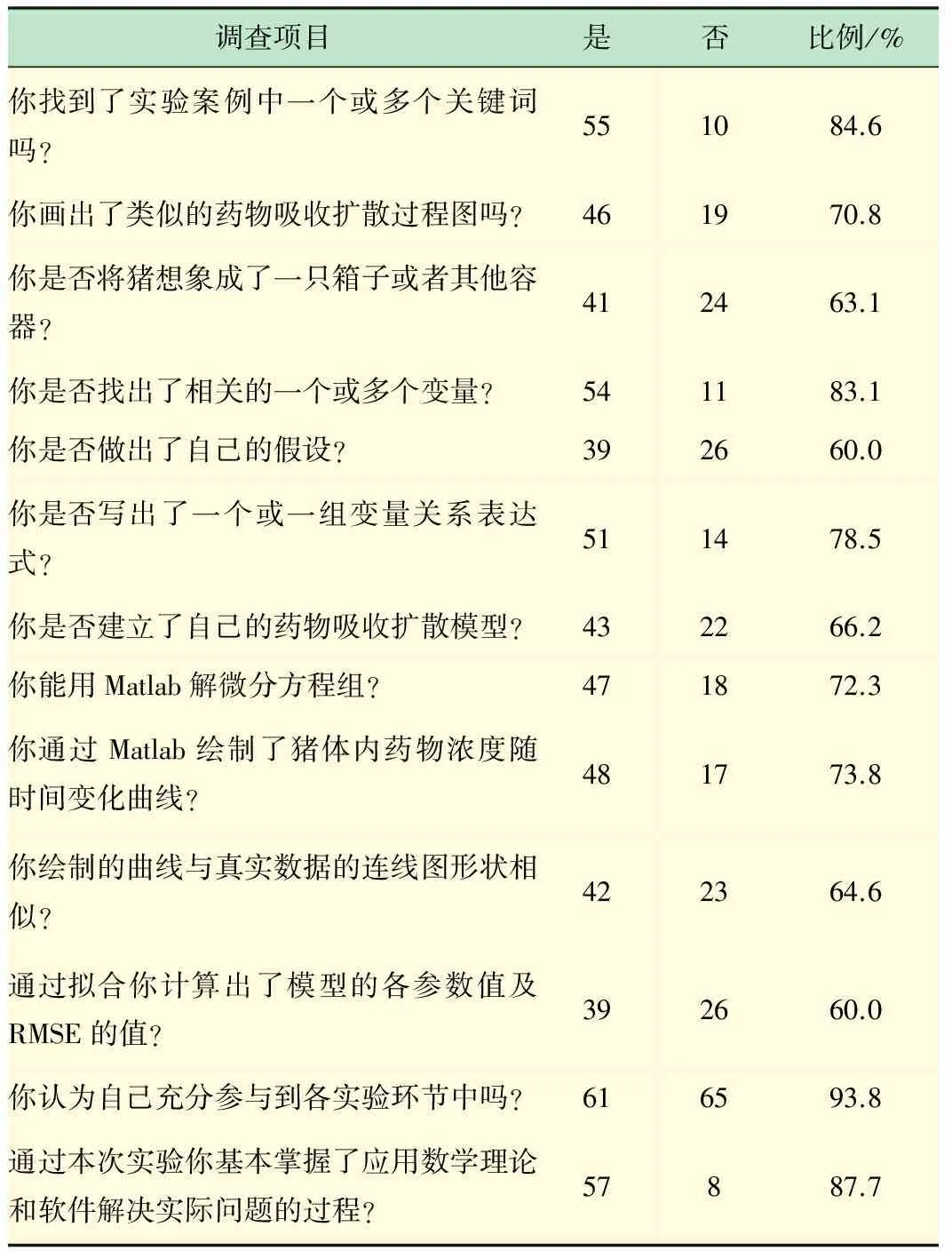
表1 实验教学效果反馈调查表

4 结 语

在建构主义理论指导下，笔者探讨了数学实验课的教学设计和实施策略，为数学实验课的教学创新做了有益的尝试，实践表明教学效果良好。建构主义下的数学实验课围绕着学生的数学实践活动展开，让学生亲历并主导运用数学知识解决实际问题的全过程，同时在自主探索中让学生的抽象和逻辑思维能力得到充分锻炼，在团队协作中加强了学生的合作交流意识，从而改善了实验课教学效果，提高了实验课教学水平，这符合当代高等教育的发展方向。

[1] 姜启源. 数学实验与数学建模[J].数学的实践与认识, 2001,31(5):613-617.

JIANG Qi-yuan. Mathematical Experiments and Mathematical Modeling[J]. Mathematics In Practice and Theory, 2001,31(5):613-617.

[2] 孙延洲.试论数学实验的教学价值[J] . 教育研究与实验,2010(6):44-47.

SUN Yan-zhou. Discussion on the Teaching Values in Mathematical Experiments[J]. Educational Research and Experiment, 2010(6):44-47.

[3] 罗 汉,万 中,王利平.数学实验课程的内容体系及教学模式[J]. 数学理论与应用,2001, 21(4):105-107.

LUO Han,WAN Zhong, WANG Li-ping. The Content and Teaching Model of the Course of Mathematical Experiments[J]. Mathematical Theory and Application, 2001, 21(4):105-107.

[4] 曹一鸣. 数学实验教学模式探究[J]. 课程·教材·教法,2003(1):46-48.

CAO Yi-ming. Exploration on the Teaching Model in Mathematical Experiments[J]. Curriculum, Teaching Material and Method, 2003(1):46-48.

[5] 但 琦,杨廷鸿,吴松林. 论大学数学实验课的教学设计[J]. 大学数学,2010, 26(5):2-5.

Dan Qi, Yang Ting-hong, WU Song-lin.Teaching Designing of Mathematic Experimental Curriculum in College[J]. College Mathematics, 2010, 26(5):2-5.

[6] 马金凤. 案例教学模式在“数学实验”课程教学中实施的实践与思考[J]. 伊犁师范学院学报,2010(2)：21-23.

MA Jin-feng. The Practice and Thinking of the Case Teaching Model and Teaching Method in Mathematics Experiment[J]. Journal of Yili Normal University(Natural Science Edition), 2010(2)：21-23.

[7] 王金然,赵童娟,郭亚君. 高校数学实验课实施现状分析及教学模式探讨[J].大家,2012(16):226-228.

WANG Jin-ran, ZHAO Tong-juan. Analysis of the Current Implement Status and Exploration on the Teaching Model in Mathematical Experiments at Colleges[J]. Master, 2012(16):226-228.

[8] 许建强,乐经良,胡良剑. 国内数学实验课程开设现状的调查分析[J].大学数学，2010, 26(4):1-3.

XU Jian-qiang, LE Jing-liang, HU Liang-jian. Investigation and Analysis of the Present Offering Status of the Course of Mathematical Experiments in China[J]. College Mathematics, 2010, 26(4):1-3.

[9] 张卫明.数学实验教学与传统课堂教学的差异性分析[J].中国数学教育，2012(12):16-18.

ZHANG Wei-Ming. Analysis of The Difference between Traditional Class Teaching and the Teaching in Mathematical Experiments[J]. Journal of Chinese Mathematics Education, 2012(12):16-18.

[10] 陈 琦,刘儒德.当代教育心理学[M].北京：北京师范大学出版社，2001.

[11] 刘素丽. 建构主义环境下大学数学实验教学浅析[J].考试周刊，2012(45)：252-253.

LIU Su-li. A Tentative Analysis of Teaching in Mathematical Experiments at Colleges under Constructive[J]. Journal of Examination, 2012(45)：252-253.

[12] 谢治州,罗晓宾,罗 琼.国内高校数学实验教学的现状分析与研究[J].教育与职业，2012(26):112-114.

XIE Zhi-zhou,LUO Xiao-bin, LUO Qion. Analysis of the Present Status of Teaching Mathematical Experiments at Domestic Colleges[J].Education and Vocation, 2012(26):112-114.

[13] 张国权.数学实验[M]. 北京：中国科学出版社，2008.

[14] 丁焕中,曾振灵,冯淇辉. 沙拉沙星在猪体内的药动学研究[J]. 畜牧兽医学报，2002(1):55-58.

DING Huan zhong,ZENG Zhen ling,FENG Qi hui. Pharmacokinetic Studies of Sarafloxacin in Pigs[J]. Chinese Journal of Animal and Veterinary Sciences, 2002(1):55-58.

[15] 顾明远. 世界高等教育发展的基本趋势和经验[J]. 北京师范大学学报，2006(5):26-34.

GU Ming-yuan. Trend and Experience of the World Higher Education Development[J]. Journal of Beijing Normal University(Social Sciences), 2006(5):26-34.