Matlab仿真在舰艇水下辐射噪声数值预报教学中的应用

杨琼方, 王永生, 魏应三, 庞之洋

(海军工程大学 动力工程学院,湖北 武汉 430033)

0 引 言

“舰艇水下辐射噪声数值预报”是轮机工程专业新开设的一门研究生课程，是为了适应当前发展海洋强国的国家战略和重点做好水面舰艇和潜艇减振降噪工作的海军发展规划而开设的专业课程。该课程的目的是让轮机工程专业的研究生具备舰艇动力装置声学性能顶层设计和总体规划的视野，掌握舰艇结构辐射噪声和直接辐射噪声的数值预报思路，了解并熟悉舰艇水下辐射噪声四大类噪声源——结构噪声(包括机械噪声和流固耦合激励噪声)、推进器直发声、流致噪声、推进器射流噪声常用的理论模型、数值预报方法、较为成熟的商用软件和应用程序、以及当前各类噪声源在国内外的发展现状，让学员在走上舰艇工作岗位后在反潜和编队协同训练及作战中具备更好的协同和配合模块化意识，能够从舰艇声学性能维持和抑制的角度对舰艇训练和作战提出更多有指导性的建议，从而更有力地提升舰艇战斗力。

笔者所在轮机工程专业是国家重点学科和省重点学科，目前具有:①舰船动力装置总体设计、系统分析、科学管理和战斗使用，②舰船动力装置振动噪声控制，③舰船动力装置自动化与仿真技术，④舰船动力装置状态检测、故障诊断与维修技术，⑤舰船新型和特种辅助机械共五个研究方向，所培养的硕士研究生毕业后主要岗位是舰艇机电部门，直接负责舰艇动力装置的日常管理与战斗使用。但是，在已使用多年的与动力装置最为紧密相关的研究生教材“现代舰船轮机工程”和“现代仿真技术及其在轮机工程中的应用”中均未涉及到舰艇四大类主要辐射噪声源的相关内容，这与当前新型潜艇设计的主要目标[1-2]和提升舰艇声隐身性能的关键技术[3-4]是不相适应的。为此，笔者所在舰船推进新技术研究室于2012年新开设了该课程。经过2年的摸索与总结，现已成功将Matlab仿真、专业噪声预报软件Virtual Lab Acoustics和Actran、以及振动与噪声分析通用软件Ansys用于该课程的教学，取得了较好的效果。笔者博士学位论文[5]“潜艇流噪声和推进器噪声的数值预报和分析”以大学排名第1被评为湖北省优秀博士学位论文，笔者指导的学士学位论文[6]“理想声源和螺旋桨辐射噪声场的动态可视化仿真分析”被评为湖北省优秀学士学位论文，笔者协助指导的硕士学位论文[7]“潜艇及其螺旋桨粘性流场与流动噪声计算”被评为大学和海军优秀硕士学位论文，这些实践应用很好地扩充和反哺了该课程教学内容设置的科学性与合理性。

Matlab仿真作为理解基本声源辐射噪声传播特性的便利工具之一，由Matlab仿真实现不同噪声源声波动方程的数值求解以及探索大型任务的可行并行算法也是自主研发舰艇辐射噪声数值预报软件或程序的必经之路。为此，本文基于Matlab的人机交互界面设计技术GUI建立了一个理想多极子声源和螺旋桨辐射噪声场的教学演示平台，该平台能够动态展示单个及多个单极子声源、偶极子声源和四极子声源辐射发声，管道中的多极子声源发声、存在墙面反射时的多极子声源发声、多个分布式多极子声源发声、螺旋桨促动盘辐射发声以及真实螺旋桨离散线谱噪声。实际课堂教学效果和问卷反馈表明，该平台很好地弥补了舰艇动力工程专业本科毕业学员没有学过一门与辐射噪声相关的专业课程的缺陷，有效地克服了声学知识本身理论性强、公式复杂、抽象难懂的现实困难，为研究生学员进一步深入探索螺旋桨和组合式推进器辐射噪声数值预报、辐射噪声的尺度效应分析以及低噪声推进器设计奠定了基础。

1 舰艇水下辐射噪声数值预报教学内容设置

舰艇水下辐射噪声数值预报是一门学科专业课程，共40学时，以讲座、研讨和上机操作的方式进行。该课程主要设置有:①水下辐射噪声基础;②流致噪声和流激噪声预报;③螺旋桨无空化和有空化噪声预报;④机械振动噪声预报;⑤流固耦合噪声预报五大模块。旨在使研究生学员建立起舰艇水下辐射噪声实船测量和数值预报技术的基本框架与知识体系，掌握四大类噪声源各自的数值预报方法、常用数值预报软件、当前的技术状态和关键技术所在。主要应用的专业工具为Matlab仿真在基本声源和螺旋桨噪声中的应用、Virtual Lab在流致噪声和推进器直发声中的应用、Actran在射流噪声中的应用以及Ansys在结构噪声中的应用。总体要求学员对商用软件的操作使用有较强的领悟能力，能够在第一学期公共课程学习期间付诸较多的时间来学习相关应用软件的操作使用。课程考核方式为针对某类噪声源提交具体的研究报告，报告中应含有针对基本算例的可信性分析。作为整个课程教学的基础，下文主要是针对Matlab仿真进行阐述。

2 多极子声源辐射噪声的动态可视化仿真

从声源机理上看，螺旋桨辐射噪声是厚度噪声、负载噪声和湍流噪声三者的迭加，它们分别对应为单极子声源、偶极子声源和四极子声源发声[8]。这三种基本声源通常统称为多极子声源，具体就是指单极源、偶极源、横向四极源和纵向四极源。尽管这三种基本声源的远场理论声指向性已经在经典声学教材中描述得非常清楚[8-10]，但对于缺少噪声背景知识的学生来说，教材中给出的静态等值线图对于真实反映噪声随时间变化的动态传播特性是不足的。Matlab仿真可以很好地弥补这一不足。同时，理解多极子声源辐射噪声的传播特性也是分析螺旋桨辐射噪声的基础。

单极源是最简单的点声源，其特征是声远场无指向性，其远场声压表达为：

(1)

其中:Q为噪声源强;ρ为流体密度;c为声速;k=2π/λ=ω/c为波数;λ为波长;ω为角频率;r为点声源到声接收点的距离;A为与频率相关的幅值系数。为便于仿真实现，令系数A=1，且引入无量纲时间尺度t′=ωt和空间尺度r′=kr，则其无量纲远场声压表达式为：

(2)

偶极源由两个间隔无穷近、等强度、同频反相的单极源组成，远场声压表达为[10]：

(3)

其中:d为两个点源间距离，θ为相对于横向x轴的指向性方位角。与单极源对应，偶极源的无量纲远场声压表达式可由单极源声压相对于偶极轴的导数得到，表示为：

(4)

四极源的辐射声功率正比于声源频率的6次方，其无量纲远场声压可由单极源的二阶导数得到：

(5)

其中，j和k为坐标分量，当j≠k时为横向四极源，当j=k时为纵向四极源。

依据式(2)～(5)，由Matlab编程求解得到单个多极子声源在某个时刻的声压云图分布如图1所示。图中红色代表声高压区、兰色代表声低压区，声源波长均为2π。可知，仿真得到的声压云图分布与经典声学教材给出的声压级理论声指向性规律[8-10]完全一致，表明用于仿真的数学模型是正确的。若将不同时刻的声压云图分布以每桢的形式记录下来，再以循环语句的方式进行播放，则可以清晰再现单个多极子声源动态辐射噪声的画面，给学生非常强烈的视觉冲击，从而加深印象。

若将单个多极子声源进一步扩充到多个多极子声源，利用声源间的同相或反相叠加，则可以得到如图2所示的5个单极源随时间变化的辐射声压场以及图3所示的5个偶极源在某个时刻的辐射声压场。因实际舰艇装备辐射发声时一定存在管道或者是壁面的反射影响，为了使教学内容具有工程适用性，再将刚性墙面反射和有限长直管内的单极源和偶极源辐射发声融入到示教平台中来。

(a) 单极源

(b) 偶极源

(c) 横向四极源

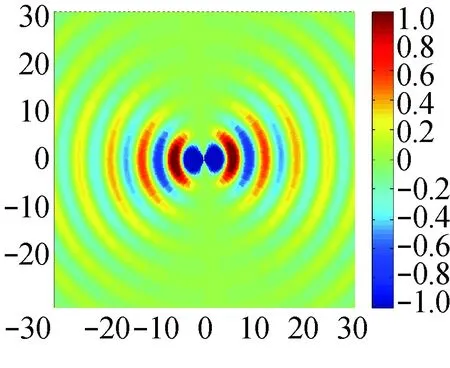
(d) 纵向四极源

(a) t1

(b) t2

(c) t3

(d) t4

(a) 同相

(b) 两两反相

刚性平面对于多极子声源的声反射作用可等价于一个声反射面，即相当于原声源与镜相声源的直接迭加[8]。仿真得到距刚性平面距离为π的单极源和偶极源的声压云图分布如图4所示。图中，刚性平面位于y轴。偶极源仅给出了偶极轴平行于刚性平面的仿真结果。原因是：与均匀来流条件下螺旋桨主要Gutin噪声指向性不同的是，伴流场中螺旋桨负载噪声呈现轴向强于径向的偶极源特征[11]，即偶极轴近似与螺旋桨旋转轴平行，也就是与船体底板平行。可以看出，因反射面的影响，无论是单极源还是偶极源，在船尾轴向都存在强声压区。单极源在螺旋桨垂向方向存在大范围强声压区，而偶极源在约45°方向存在强声压区，这也是舰尾螺旋桨噪声监测仪通常布置于桨前方与轴向成45°的原因之一。这些声学现象在目前已有的轮机工程专业教材中是没有的。

(a) 单极源

(b) 偶极源

图4 离刚性平面距离为π的单极源和偶极源声压云图

对于导管内声源发声来说，可取直导管轴向为x轴、径向为y轴。有限长直导管中单极源的辐射声压表达式为[12]：

(6)

y0为声源距导管中心轴线的径向距离。

当导管中声源为偶极源时，同样仅分析偶极轴与导管轴向平行的仿真结果。此时，辐射声压表达式为[12]：

(7)

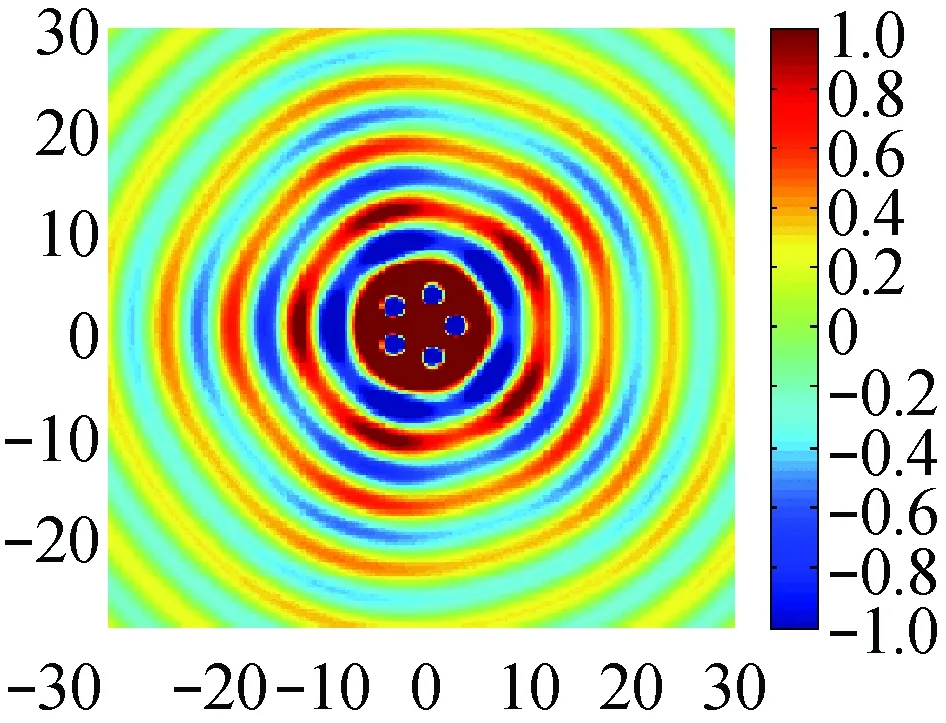
仿真得到单极源在某时刻的声压云图分布如图5(a)所示。可以看出，在单极源的径向对称位置处存在明显的双弱声压区，与刚性平面下方近距离的单极源声场特征差异明显。仿真得到某时刻导管内偶极源声压云图分布如图6所示。可以看出，在亥姆赫兹数为3π/2时，导管对偶极源径向声压有明显的抑制作用，而当亥姆赫兹数为π/2时，该抑制作用并未出现，该结论与文献[13]中得出的导管仅在中高频段对螺旋桨噪声具有明显屏蔽效果的结论一致。可以看出，该示教平台可以很好地将科研融入课堂教学。

(a) k′=3π/2

(b) k′=π/2

(a) k′=3π/2

(b) k′=π/2

3 螺旋桨促动盘辐射声场Matlab可视化仿真

促动盘是真实螺旋桨桨叶轴向投影的一个简化，分析促动盘辐射声场可以间接反映螺旋桨的宽带谱噪声性能。在实际螺旋桨方案设计阶段时，往往仅确定了桨叶直径，而并没有具体确定桨叶几何形状。此时若将分布式多极源置于一个无穷薄的旋转盘面上，则给定转速下的螺旋桨促动盘辐射发声可以进行评估以及进行动态可视化显示，它将能够用于比较所设计螺旋桨主要参数的噪声性能优劣。

与噪声测量和计算流体动力学分析时设置对应，螺旋桨和声接收点在计算域中均处于静止，而轴向来流对应为来流马赫数M∞，桨叶周向旋转对应为周向马赫数Mt=RΩ/c(R为桨半径，Ω为旋转角速度)。若取z轴为螺旋桨旋转轴，z轴负向为来流方向，桨盘面位于z1=0处。当声压以ρc2、速度以c进行无量纲化后，得到单位半径促动盘辐射声场在频率内的积分解为[14]：

(9)

(10)

式中：n为负载噪声和厚度噪声频率谐次；r0为无量纲桨毂半径；波数k=nMt；hn为桨叶几何的傅利叶变化谐次，分析时取为1；gn为轴向推力的傅利叶变化谐次；R″为声源与声接收点之间距离；σ为点声源相半径；pT和pL分别为厚度噪声和负载噪声分量。该式中忽略了桨叶在周向旋转过程中水流阻滞作用对负载噪声的贡献。当计算得到I和L两个积分函数后，即可得到厚度噪声和负载噪声声压分布以及某个测点处的声压级大小。

图7所示为某七叶桨促动盘盘面内厚度噪声和负载噪声的瞬时声压场。此时，叶频(BPF)的谐次数n=3.5、0≤r≤3、-3≤z≤3。可以发现，厚度噪声分量的贡献主要集中于叶梢外部区域，而负载噪声分量主要集中于叶面区间(r<1)。盘面内声瓣状特征非常明显，并且，因对应极低马赫数流动，叶梢外部区间的声旋转效应不如文[15]中得到的近临界音速(Mt=0.7)的声场特征明显。为证明仿真结果的正确性，将周向马赫数增加到0.7，此时来流作用相对可忽略不计，可理解为螺旋桨的系泊高速空转状态，对应的盘面内声压特征如图8所示，此时旋转作用对声场的贡献占主导作用，所得现象与文[15]中结论一致。

(a) pr

(b) pL

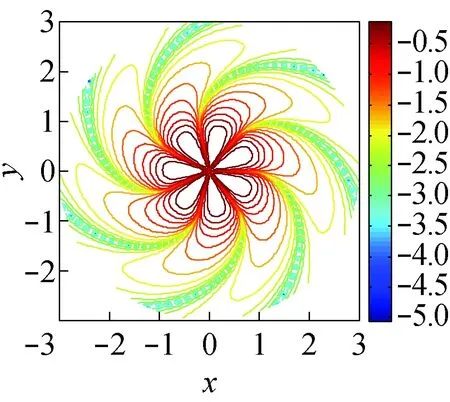
(a) pr

(b) pL

4 螺旋桨线谱噪声预报的教学案例

为便于教学实践和工程应用，基于Matlab软件中的图形用户界面(GUI)设计，将单个多极子声源辐射噪声、分布式多极源辐射发声、刚性平面和有限长导管反射条件下的多极源辐射发声、螺旋桨促动盘辐射发声以及螺旋桨积分脉动力源辐射发声开发了一个能够进行动态可视化显示的教学演示平台，如图9所示，每个子模块可方便快捷调用。当选中某个子模块后，界面会提示需要输入参数，同时会显示对应的数学模型以及动态模拟效果。

图9 多极源和螺旋桨辐射噪声场动态可视化分析界面

对于船用螺旋桨来说，它与气动转子的显著差别是工作于周向非均匀进流条件，且来流马赫数极低。经典声学教材中给出的脉动力源远场辐射声压表达式为[8]：

(11)

式中:t′为迟滞时间;F为脉动力;r为脉动力源到测点距离;θ为F与r矢量之间夹角;cosθ项用于表征脉动力源的偶极声场指向性。该式表明：一旦脉动力源幅值确定，则该声源的谱源级确定。因此，基于式(11)，只要在演示平台中输入不同谐次频率下的脉动力幅值，即能得出不同线谱处的谱源级值，非常直接。

5 结 语

舰艇水下辐射噪声知识理论性强、抽象难懂、数学模型和物理现象均十分复杂，物理试验的条件要求也非常高，是当前舰艇声隐身性能提升的关键技术之一，也是水声工程课程教学的难点之一。本文利用Matlab工具搭建了一个多极子声源和螺旋桨辐射噪声场动态可示化仿真的教学演示平台，可以直观显示不同声源辐射发声的数学模型和空间动态声辐射效果，使学员形象感知并理解声源辐射发声特点，能够显著提升教学效果。该平台是舰艇四大类噪声源可视化分析工具之一，具有可扩展性。下一步将继续融合其他三类噪声源声场可视化图像，构建一个完整的舰艇水下辐射噪声教学实验系统。

[1] Joubert P N．Some aspects of submarine design．Part2：shape of a submarine 2026[R]. Defense Science and Technology Organization, Australian, 2006.

[2] Joubert P N．Some aspects of submarine design．Part1：hydrodynamics[R]. Defense Science and Technology Organization, Australian, 2004.

[3] DARPA TANGO BRAVO. 16 February 2011, USA. http://www.darpa.mil/sto/programs/tango/index.html.

[4] Heberley B D. Analysis of the operational impacts of alternative propulsion configurations on submarine maneuverability[D]. USA: MIT, 2011.

[5] 杨琼方. 潜艇流噪声和推进器噪声的数值预报和分析[D]. 武汉: 海军工程大学, 2011.

[6] 甘克涛. 理想声源和螺旋桨辐射噪声的数值仿真与动态可视化分析[D]. 武汉: 海军工程大学, 2013.

[7] 曾文德. 潜艇及其螺旋桨粘性流场与流动噪声计算[D]. 武汉: 海军工程大学, 2009.

[8] Ross D. Mechanics of underwater noise[M]. New York: Pergamon Press, 1976.

[9] Carlton J S. Marine propellers and propulsion[M]. Second Edition, Netherlands: Elsevier LTD, 2007.

[10] Russell D A, Titlow J P, Bemmen Y J. Acoustic monopoles, dipoles, and quadrupoles: an experiment revisited[J]. Am J Phys, 1999, 67(8): 660-664.

[11] Seol H, Suh J C, Lee S. Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of Sound and Vibration, 2005, 288(2): 345-360.

[12] Rienstra S W, Hirschberg A. An introduction to acoustics[R]. Eindhoven University of Technology, 2013.

[13] 熊紫英, 朱锡清, 刘小龙, 等. 船尾伴流场-导管-螺旋桨互作用噪声预报研究[J]. 声学学报, 2009, 34(2): 117-123.

XIONG Zi-ying, ZHU Xi-qing, LIU Xiao-long,etal. Stern wake-duct-propeller interaction noise prediction and research[J]. Acta Acustica, 2009, 34(2): 117-123.

[14] Carley M. Time domain calculation of noise generated by a propeller in a flow[D]. Ireland: Department of Mechanical Engineering, Trinity College, 1996.

[15] Carley M. Propeller noise fields[J]. Journal of Sound and Vibration, 2000, 233(2): 255-277.