采用输出误差符号判决的变步长常数模盲均衡

肖 瑛，阮 睿，李春杰

(1.大连民族学院 信息与通信工程学院，辽宁大连 116605;2.大连理工大学电子信息与电气工程学部，辽宁大连 116024;3.中南民族大学电子信息工程学院，湖北武汉430074)

盲均衡技术具有不需要训练序列即可实现信道补偿和跟踪的性能，消除码间干扰的同时可以有效节省通信带宽，并可防止均衡器失锁［1］。未来高速通信发展对通信质量和通信效率将具有更高的要求，盲均衡技术在未来通信中具有潜在应用价值。目前为止，各类盲均衡算法中，常数模算法(Constant Modulus Algorithm，简称CMA)是最简单和稳健的一种实用算法［2］。但是由于CMA算法本质上属于梯度下降算法，学习步长值对算法性能具有重要影响，固定步长的CMA盲均衡算法在收敛速度和收敛精度上存在矛盾，解决这一问题的有效方法就是采用变步长 CMA算法［3］。现有变步长CMA算法均是设置步长增益因子在算法迭代过程中对步长进行适时调整，而步长增益因子的计算依赖于均衡器的输出误差，即步长增益因子利用均衡器输出误差的某种非线性变换进行控制，这就需要人为设置一些合理的控制参数，一旦控制参数选择不合理，严重影响算法性能。在时变信道的均衡中，由于信道环境的变化，尤其是某种突发变化，原有设置合理的步长增益因子控制参数可能会在信道变化后并不合理，而且控制参数选择本身就缺乏理论依据。本文在分析现有变步长盲均衡算法的基础上，提出了一种采用输出误差符号判决的变步长常数模盲均衡算法，算法无需人工设置步长因子控制参数，算法简单，易于实现。在电话信道和混合相位信道条件下利用计算机仿真对方法的性能进行了验证，同时，利用信道传输路径变化模拟信道突发干扰，进一步验证了算法的稳定性。

1 CMA盲均衡

CMA盲均衡是Bussgang类盲均衡算法的一个特例，由Godard和Treichler等人提出，非常适合具有恒定包络的发射信号的均衡。在Godard算法中设置参数p=2即为CMA算法。如图1是CMA盲均衡的简单的离散信道和均衡器的等效基带模型［4］。

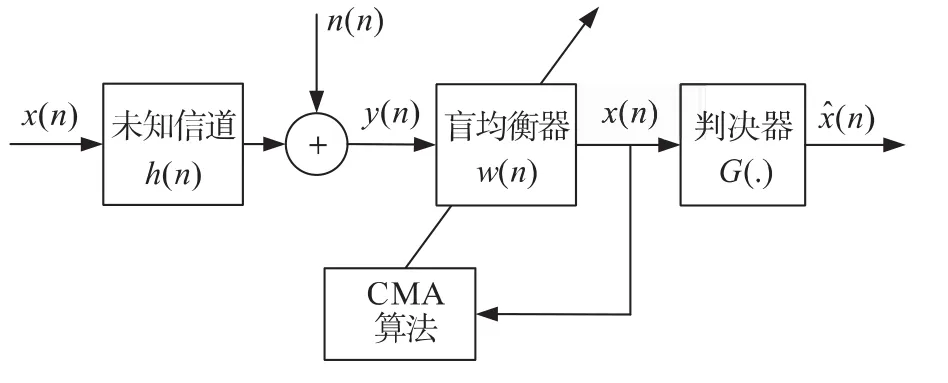
图1 CMA盲均衡基本原理框图

图1中发射信号x(n)经信道h(n)并叠加高斯白噪声n(n)，在均衡器w(n)前得到观测信号序列y(n)，盲均衡的本质就是在发射信号x(n)和信道h(n)未知的情况下，仅根据观测信号y(n)利用均衡器实现对发射信号x(n)的恢复，恢复信号˜x(n)利用判决器G(.)进行判决恢复原始发送源符号序列的估计。Bussgang类盲均衡算法是通过对均衡器的输出进行某种非线性变换，这一非线性变换满足 Bussgang过程，CMA是Bussgang类算法的一个特例，其代价函数为［5］

从CMA算法代价函数中可以看出，CMA算法间接利用信号的高阶统计量，常利用梯度下降算法实现均衡器权系数的迭代更新。根据随机梯度下降算法原理，CMA盲均衡器权系数更新公式可以写为

2 变步长CMA盲均衡

收敛速度和收敛精度是评价盲均衡算法性能的两个重要指标，对于采用随机梯度下降算法的CMA盲均衡而言，学习步长的选取对于算法的性能有重要影响。在固定步长情况下，CMA盲均衡算法的收敛速度和收敛精度难以同时保证，较大的步长值可以获得较快的收敛速度，但是收敛后稳态剩余误差大，较小的步长值可在收敛后获得较小的稳态剩余误差，但是收敛速度慢，即固定步长的CMA盲均衡算法在收敛速度和收敛精度上存在着固有的矛盾。变步长盲均衡算法的基本原理是在均衡初始阶段利用较大的步长值获得较快的收敛速度，随着算法的迭代逐步减小步长值，实现获得较高收敛精度的目的，从而算法性能在较大步长值和较小步长值之间取得折中。变步长CMA盲均衡的均衡器权值迭代公式可以在式(5)的基础上进行修改得到

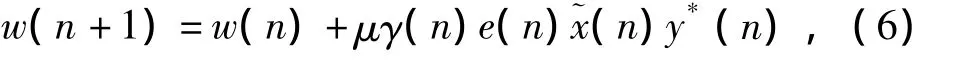
其中γ(n)为步长增益控制函数，并且有1≥γ(n)＞0。γ(n)控制着步长的变化比例，变步长CMA盲均衡算法的关键就是调整γ(n)来实现对步长值变化的控制，理想的步长增益γ(n)应该满足在初始情况下γ(n)→1，随着算法的迭代收敛，γ(n)逐渐趋于0。

在目前已有的变步长算法中，大多是根据均衡器的输出误差的某种非线性变换来控制步长增益 γ(n)，典型的几种算法包括［7－8］:

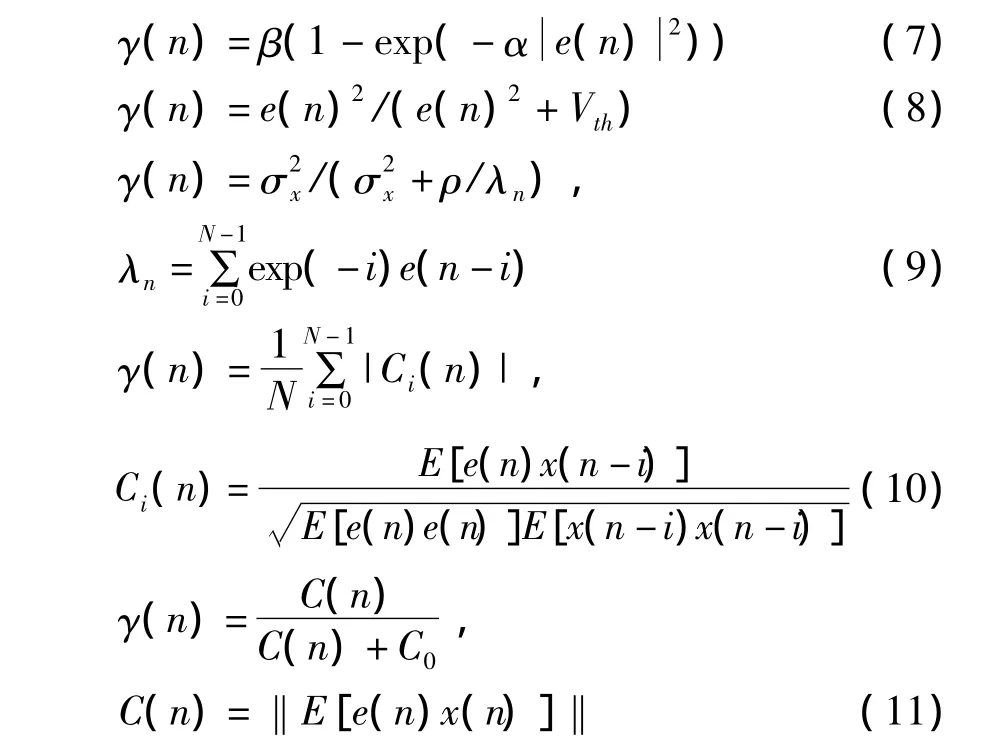
在上述变步长算法中 α，β，Vth，ρ，C0均为待定参数，需要人工经验设置，e(n)表示误差信号，σx为输入信号的标准差，E［.］表示数学期望。宋等人在对现有变步长算法的基础上进行了理论分析，指出上述变步长算法都难以保证初始情况下步长增益γ(n)→1的条件，并提出了一种新的变步长算法［9］，算法的步长因子计算公式为

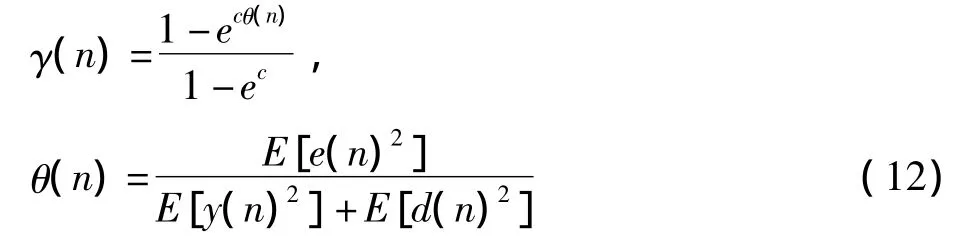
式中c为经验常数。在CMA盲均衡算法中，式(12)中的期望输出d(n)可以用常模R2代替，这种方法可以保证在算法初始阶段γ(n)→1，并且满足变步长算法步长变化规则的需求。

分析上述变步长算法可以看出，步长增益因子γ(n)的控制函数里均包含的误差或者输出信号的功率等参数，并且在非线性变换中常需设置一些调整参数。由于自适应算法在迭代过程中逐次接收的数据样本往往非常有限，并且通信信道常常伴随噪声干扰，这使得在迭代过程中逐次估计输出误差和信号的功率等信息时得不到准确信息，非线性变换过程中需要人为设置的参数往往不具有通用性，即对不同的通信信道条件，这些参数往往不同。在此基础上，文中设计了一种新的变步长CMA盲均衡算法，步长控制增益因子γ(n)不依赖于接收信号和误差信号的信息进行调整，并且无需额外设置调整参数，算法步长因子计算公式如下:

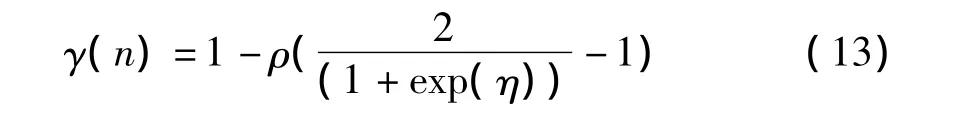
式(13)中，ρ为最大步长值对应的数量级，η为在CMA准则和DD准则下输出误差符号的一致性次数与迭代次数的比值。DD盲均衡算法的代价函数为

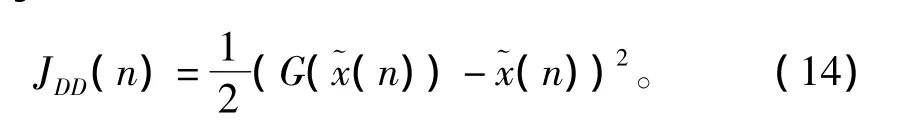
令DD盲均衡算法的误差函数为

则在DD盲均衡算法均衡器的更新公式为:

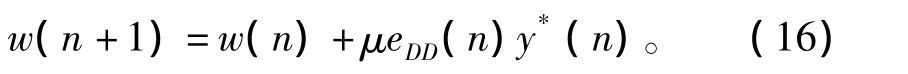
如果盲均衡算法收敛，则根据CMA准则和DD准则计算的误差具有一致性，因此可以利用eDD(n)与e(n)的符号是否一致来判断均衡器输出信号的星座图是否打开，即算法是否收敛。变步长盲均衡算法在收敛后，需要较小的步长获得较高的收敛精度，因此可以利用eDD(n)与e(n)符号一致的频次来判断算法是否收敛，在这一思想设计的变步长盲均衡算法中的步长增益因子控制参数为

式中N为当前迭代次数。根据步长增益因子γ(n)的定义以及CMA准则和DD准则在盲均衡算法中的误差性质，可以得到新的变步长CMA盲均衡算法

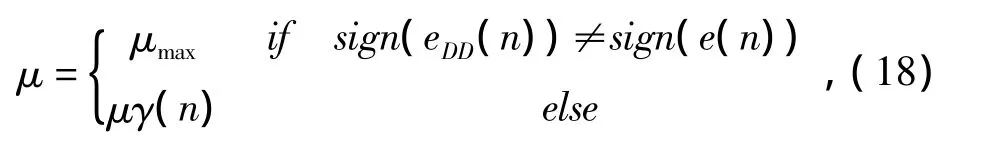
根据式(18)定义的变步长调整原则，如果在CMA准则和DD准则计算误差符号一致，那么对应的控制步长增益因子γ(n)的参数η的频次加1，并且步长值进行在γ(n)作用下减小。否则，认为算法尚未收敛，保持最大步长值进行均衡器权系数调整，以获得较快的收敛速度。随着均衡算法的迭代收敛，eDD(n)与e(n)的符号一致频次越来越高，完全收敛后达到一致，在此过程中，步长值随着误差符号一致频次逐渐减小，实现获得高收敛精度的目的。

由输出误差符号判决的变步长常数模盲均衡算法步长的变化控制参数中可以看出，步长值的调整不依赖于误差的非线性变换，步长增益因子γ(n)的控制参数ρ和η均可以在程序中计算，并且在算法初期可以保证γ(n)=1，无需人工设置。由于当误差符号不一致时，步长值自动切换到大步长值，因此算法在信道突发干扰的情况下依然可以保持快速收敛。

3 计算机仿真

为验证输出误差符号判决的变步长常数模盲均衡算法，利用仿真电话信道和混合相位信道进行仿真实验。发送信号采用等概率二进制序列生成，经QPSK调制，仿真电话信道的基带冲激响应为

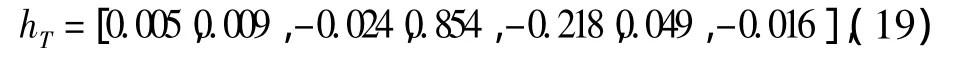
混合相位信道的基带冲激响应为

接收观测信号叠加零均值带限高斯白噪声，信噪比SNR=20dB，均衡器长度为32。定义剩余码间干扰ISI来对算法性能进行评价［10］:

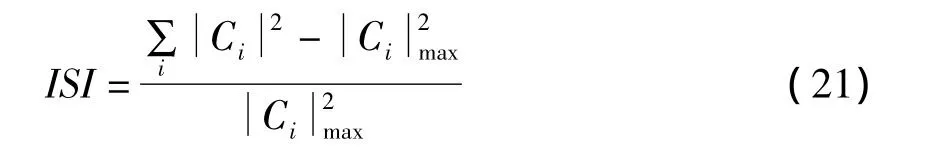
图2 电话信道下仿真结果

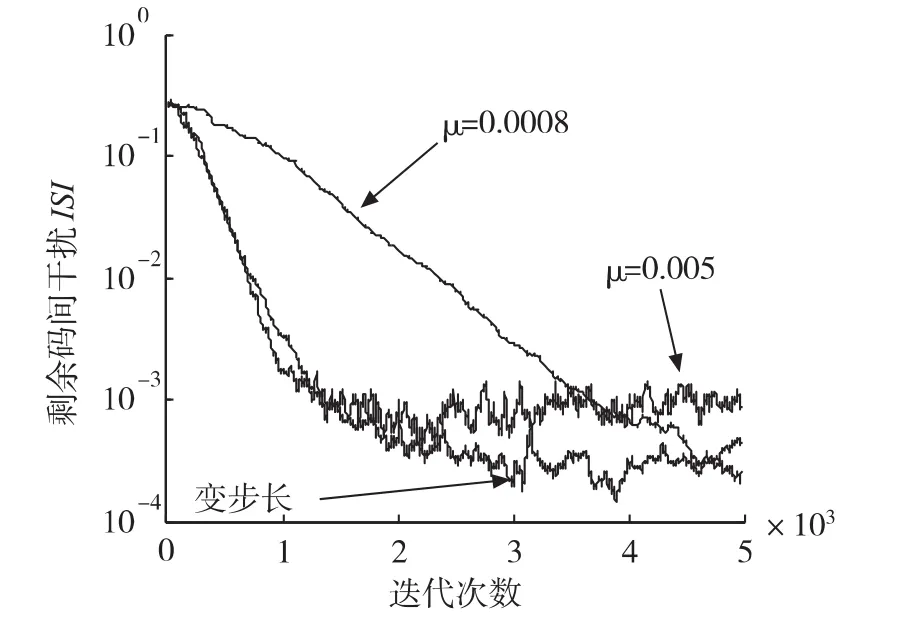
图3 混合相位信道下仿真结果

其中，Ci为信道与均衡器的联合冲激响应。两种信道条件下的仿真结果分别如图2和图3。为进一步验证算法对抗信道突发变化的适应性能，在算法迭代至5000次时，利用混合相位信道反射路径反相模拟信道突发干扰，即信道模型由hM切换至:利用误差符号判决的变步长常数模盲均衡算法获得仿真结果如图4，对应的步长值的变化如图5。

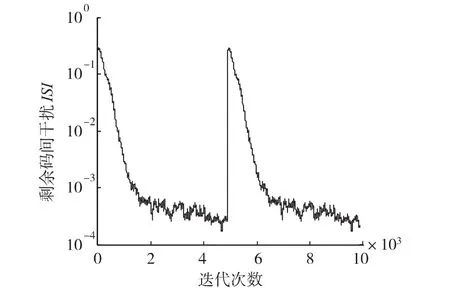
图4 突发干扰信道仿真

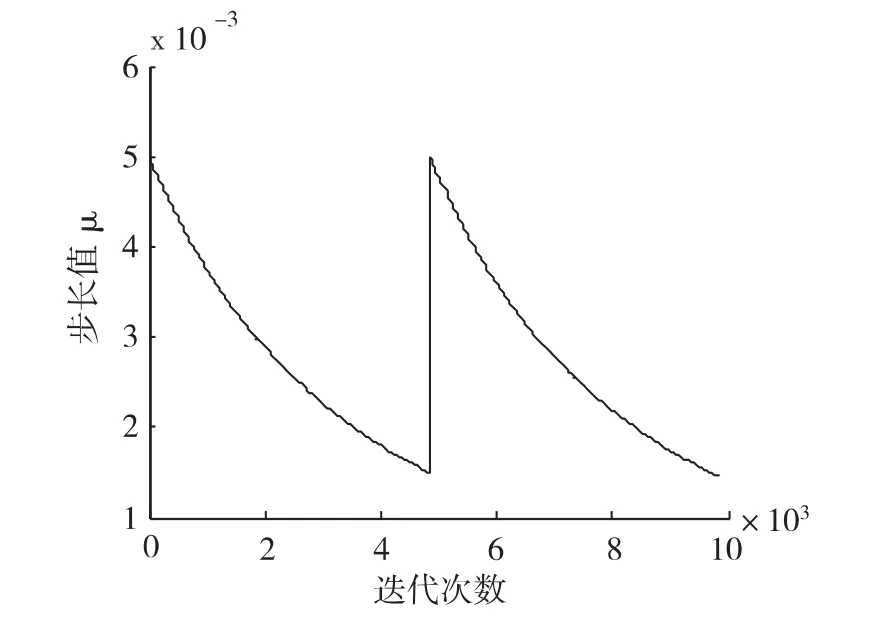
图5 步长值变化趋势曲线

由图2和图3种可以看出，文中提出的误差符号判决的变步长常数模盲均衡算法在收敛初期可以获得与大步长接近的收敛速度，收敛后可以获得更高的收敛精度。从图4和图5中可以看出，在信道发生突发变化情况下，步长可以迅速调整到大步长值，保证算法快速收敛并可在收敛后具有较高的收敛精度。

4 结语

文中在对现有变步长算法分析的基础上，提出了一种误差符号判决的变步长常数模盲均衡算法，步长增益因子由最大步长值的数量级以及在CMA准则和DD准则下计算得到的误差符号一致性的频数来控制，因此误差符号判决的变步长盲均衡算法的步长调节过程中无需人工设置额外参数，具有更为广泛的适用性。根据对步长增益因子的分析，文中提出的步长增益因子在初期为1，随算法迭代过程逐步下降，且当信道突发变化时可迅速转入大步长值进行均衡器权系数更新，因此满足变步长算法要求的理想步长增益因子需求，计算机仿真结果验证了算法的有效性。

［1］HWANG K，CHOI S.Blind equalizer for constantmodulus signals based on Gaussian process regression［J］.Signal Processing，2012，92(6):1397 －1403.

［2］DEMISSIE B，KREUZER S.Performance predictions for parameter estimators that minimize cost－functions using wirtinger calculus with application to CM blind equalization ［J］.IEEE Transactions on Signal Processing，2011，59(8):3685－3698.

［3］周俊，刘鹏，曹素芝，等.改进的变步长抖动符号误差常数模算法［J］.仪器仪表学报，2011，32(3):701－706.

［4］黄蕾，杨绿溪.一种新的基于统计测度的变步长CMA盲均衡算法［J］.数据采集与处理，2003，18(1):62－65.

［5］NEVES A，PANAZIO C.A class of channels resulting in Ill－convergence for CMA in decision feedback equalizers［J］.IEEE Transactions on Signal Processing，2010，58(11):5736－5743.

［6］肖瑛，董玉华.并联滤波的常数模与判决引导融合盲均衡算法［J］.声学学报，2012，37(5):495－500.

［7］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094－1097.

［8］HYUN－CHOOL S，ALI H S，WOO －JIN S.Variable Step － Size NLMS and Affine Projection Algorithms［J］.IEEE Signal Processing Letters，2004，11(2):132 －135.

［9］宋彦，汪萌，戴礼荣，等.一种新的变步长自适应滤波算法及分析［J］.电路与系统学报，2010，15(4):70－74.

［10］CHEN S，COOK TB，ANDERSON LC.A comparative study of two blind FIR equalizer［J］.Digital Signal Processing，2004，14(1):18 －36

(责任编辑 刘敏)