一种同态验证环签名方案的安全性分析与改进

高雪辰，郭显久、2

(1.大连海洋大学信息工程学院，辽宁大连116023;2.辽宁省海洋信息技术重点实验室，辽宁大连 116023）

一种同态验证环签名方案的安全性分析与改进

高雪辰1，郭显久1、2

(1.大连海洋大学信息工程学院，辽宁大连116023;2.辽宁省海洋信息技术重点实验室，辽宁大连 116023）

对2012年Wang等提出的一种新的应用于云计算的共享数据可公开审计方法中的同态验证环签名方案进行了分析。结果表明，该方案容易受到群成员改变攻击，并且给出了攻击方法。为了防止攻击，对该方案进行了改进，并对新方案做了安全性分析，证明其具有安全性。

环签名;双线性对;公开审计

环签名的概念最早由Rivest等［1］在2001年提出，最初的环签名方案思想是基于RSA公钥密码体制。此后，很多研究者相继提出了各种环签名方案［2－4］，继而使环签名得到了较为广泛的应用。与一般的数字签名不同，环签名最吸引人的地方在于它的不可伪造性和无条件匿名性。

2007年，Ateniese等［5］第一次提出了在云计算环境下的可证数据持有性 (provable data possession，PDP）模型。该PDP模型主要运用了同态理论以及RSA公钥密码体制，实现了远程数据持有性证明，并且大大减少了证明过程中的通信量。随后PDP模型理论得到了快速发展，很多新型的远程数据 PDP 方案被提出［6－8］。

2012年，Wang等［9］将PDP模型与环签名理论相结合，提出了Oruta公开审计方法，该方法可以在云服务器上对共享数据进行公开审计，并对其用户的隐私给予保留。Oruta公开审计方法主要基于同态验证环签名方案 (HARS），可以允许一个用户群组通过TPA(第三验证方）在云服务器上公开验证共享的存储数据的完整性，而无需取回所有的共享数据。与此同时，在验证的过程中，每个具有共享数据身份的用户都可以通过TPA持有自己的私钥，以便通过TPA来公开验证共享数据的完整性。经分析发现，HARS方案其模型存在安全缺陷，本研究中对此提出了分析和改进，弥补了此方案的不足。

1 双线性对

HARS方案以及本研究改进的方案都将用到双线性对的性质。双线性对是定义于椭圆曲线上的一种映射，满足双线性性质。设G1和G2为两个乘法循环群，其阶都为质数p。令g1和g2分别为群G1和G2的生成元。令φ为从G2到G1的同构映射，即φ(g2）=g1。

双线性对e:G1×G2→GT，e满足下列条件:

(1）双线性。对于u∈G1、v∈G2和 a、b∈Z，有

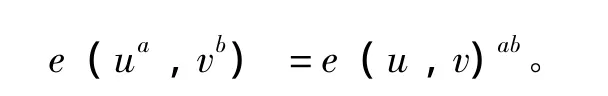
(2）非退化性。e(g1，g2）≠1。

(3）可计算性。存在有效算法计算e(u，v）。

目前，双线性对大多是基于 Weil配对［10］或Tate配对［11－12］实现的。假设 G1和 G2为两个乘法循环群，阶为p，p为G1的生成元，则解决下列问题是困难的:

(1）离散对数问题 (DLP）。任取Q∈G1，找出一个n∈，使得满足Q=Pn。

(2）计算 Diffie－Hellman问题 (CDHP）。∀ (P，Pa，Pb）∈，其中 a、b∈，求出Pab。

(3）决策 Diffie－Hellman问题 (DDHP）。∀ (P，Pa，Pb，Pc）∈，其中 a、b、c∈，判断ab≡c mod p是否成立。

(4）Gap Diffie－Hellman问题 (GDHP）。一类CDHP解决困难而DDHP解决容易的问题。

(5）双线性逆 Diffie－Hellman问题(BIDHP）。∀ (P，Pa，Pb）∈，其中 a、b∈，计算e(P，P）ab－1。

(6）逆Diffie－Hellman计算问题 (Inv－CDHP）。∀ (P，Pa）∈，其中 a∈，计算Pa－1。

2 文献 ［9］中的HARS方案及其攻击方法

2.1 安全模型

HARS方案包括3种算法:KeyGen、RingSign和RingVerify。在KeyGen算法中，用户群中的每个用户都可生成其公钥和私钥;在RingSign算法中，用户群中的每个用户都可以用其私钥和其他用户的公钥对数据分组生成环签名;在RingVerify算法中，验证者可以检查一个给出的数据分组环签名对是否由该群中某一成员生成。HARS方案具有以下性质:

(1）正确性。对于给出的任意数据分组及其环签名，一个验证者都可以正确地通过该方案来检查此数据分组的完整性。

(2）不可伪造性。对于任何一个伪造者A来说，想对此方案伪造出一个环签名在计算上是不可行的。

(3）同态性。该方案是一个具有同态性质的方案，包括无阻塞验证性以及不可延展性。

(4）完全匿名性。对于任意的拥有d个用户的用户群组U，以及任意一种算法ξ来说，在U中的任意一个可以成为真实签名者的Us，用算法ξ可以计算出其真实身份的概率不超过1/d。

2.2 HARS方案

假设G1、G2和GT分别为具有相同阶p的循环乘法群，g1和g2分别由G1和G2生成。设e:G1×G2→GT为双线性对，φ (g2）=g1，H1∶{0，1}*→G1为一个哈希函数，系统参数为param=(e，φ，p，G1，G2，GT，g1，g2，H1）。用户群中的用户总数为d。

(1）密钥产生KeyGen。用户ui随机选取xi∈Zp，计算wi=∈G2。用户得到公钥pki=wi，以及相应的私钥ski=xi。

(2）环签名产生RingSign。给出用户的公钥集合 (pk1，…，pkd）=(w1，…，wd），数据分组m∈Zp，该分组的标识为 id，以及相对于用户s的私钥 sks，随机选取 ai∈Zp，i≠s，i∈ ［1，d］，令σi=。用户 (签名者）s计算β=H1(id）∈G2，使

输出环签名 σ=(σ1，…，σd）∈，L=(w1，…，wd），以及消息m。

(3）环签名确认RingVerify。当接收到环签名(L，m，σ）后，确认 e(β，g2）与e(σi，wi）是否相等。如果相等，则m是被d个用户中的一个用户签名，反之则不成立。

2.3 对HARS方案的攻击方法

通过对上述方案进行分析，发现在其安全模型中存在群成员改变的攻击方法。设σ=(σ1，…，σd）为m的环签名，伪造者A在不知道任何用户群成员私钥的情况下，可以增加Ud+1进入成员集，但仍然可以通过签名确认。

伪造者A任取t∈Zp，使得=σd+twd+1，= － twd，令= σi，i=1，2，…，n－1。消息m 的新签名为 σ =(，…，，），则新签名能够通过确认，利用双线性对的性质，证明如下:

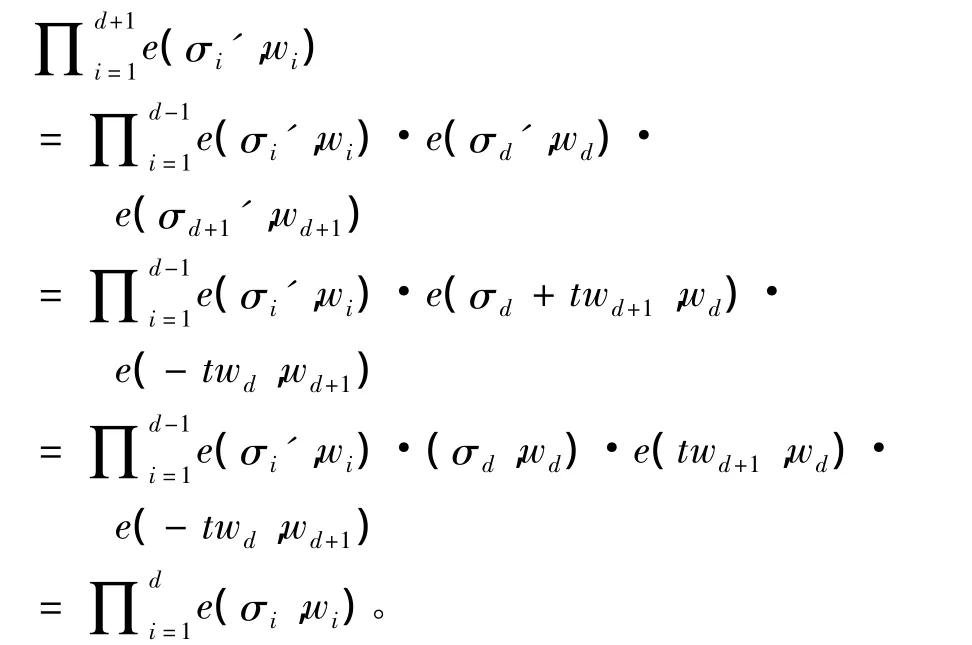
上式说明，伪造者A所伪造的环签名可以通过环签名确认RingVerify，从而成功地伪造了环签名，使得同态验证环签名方案存在群成员改变攻击。

3 对文献 ［9］中HARS方案的改进和安全性分析

3.1 改进的方案

由于HARS方案在其安全模型中存在群成员改变攻击，针对这种攻击方式，对原方案进行如下改进:在环签名产生RingSign阶段，给出所有用户的公钥集合，不妨设为 L=(pk1，…，pkd）=(w1，…，wd），数据分组m∈Zp，该分组标识为id，以及相对于用户 s的私钥sks，随机选取 ai∈Zp，i≠s，i∈ ［1，d］，计算 σi=。用户 (签名者）s计算

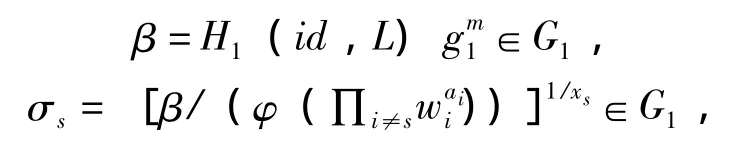
其中，L为用户群成员的公钥集合。输出环签名σ =(σ1，…，σd）∈，L=(W1，…，Wd），以及消息分组m。

3.2 安全性分析

定理1(正确性） 任意一个有效的数据分组及其环签名能够通过验证者的检测。

证明:设公钥集合 L=(pk1，…，pkd）=(w1，…，wd），能够得到:

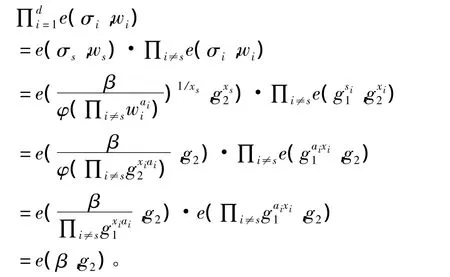
定理2(不可伪造性） 假设攻击者A能够以(t'，ε'）伪造改进的环签名，则存在一种算法，该算法能够以 (t，ε）解决BIDHP困难问题。其中，

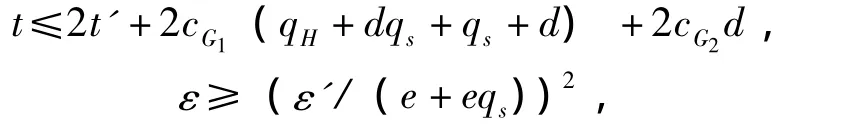
A发出至多个qH哈希请求和qs个环签名请求，e=limqs→∞(1+1/qs）qs，cG1为在 G1上运算的消耗，cG2为在G2上幂运算的消耗。

首先，B从Zp中随机选取 (x2，…，xn），并且设x1=1。然后令pki=wi= (）xi，其中pki代表用户i的公钥。A得到公钥集合L=(pk1，…，pkd）=(w1，…，wd）。不失一般性，假设 A可以为每个数据分组m、标识id和L发出环签名产生的请求和哈希请求。

在每个哈希请求中，B需要做出投掷硬币的选择，假如以概率Pc为投掷了背面，那么显示为0，否则为1。这时，B随机从ZP中选取r，如果投掷为背面0的时候，B会返回φ(）r，否则返回φ）r。

假设A对数据分组m、标识id和L发出环签名产生的请求。那么通过上述假设，一个哈希请求将在这个 (m，id，L）上发出。如果B在哈希请求中投掷了0，则B失败退出。否则，B返回H1(id，L）=φ(）r。如此，B选择随机的 a2，…，ad∈ZP，计算a1=r－ (a2x2+…+adxd），然后返回签名σ=(，…，）。

最后，A在数据分组m和标识id上输出一个伪造的签名σ=(σ1，…，σd）。再次通过之前的假设，一个哈希请求将在这个 (m，id，L）上发出。如果B在哈希质疑中没投掷0，则B退出。否则H1(id，L）=，r由B产生，B通过计算(）1/r输出。

A不能区分B的模拟和真实身份。如果A成功地伪造了签名，那么B将输出。B不失败的概率为(1－P），当Pc=qs/(qs+1）时最大，值域为 1/(e(1+qs）），e=limqs→∞(1+1/qs）qs。B算法需要做以下次运算:在设置G2上做d次取幂运算，每个A的哈希请求在G1上都做1次取幂运算，每个A的环签名生成请求在G1上都做d+1次取幂运算，以及在G1上输出做d次取幂运算。所以，B的运算时间是在A运算时间上再加cG1(qH+dqs+qs+d）+cG2d。

由于BIDHP问题可通过用B算法解决两个随机问题而得到解决，因此，如果A利用算法 (t'，ε'）生成一个拥有d个用户的群组的伪造环签名，就需要存在一种算法 (t，ε）去解决co－CDH问题，这个算法的复杂度为

但目前来说，解决co－CDH问题仍然是比较困难的，也就是说，对于攻击者A来说，伪造环签名在计算上是不可行的，所以新方案具有不可伪造性。

定理3(完全匿名性） 对于任意的拥有d个用户的用户群组L的环签名，攻击者A可以计算出其真实身份的概率不超过1/d。

证明:对于任意的h(h∈G1）和s(1≤s≤d），有 {，…，∶，i≠s，as被选择于=h}与 {，…∶=h}同分布，所以给出签名σ=(σ1，…，σd），攻击者A可计算出签名者真实身份的概率最多为1/d。

4 结语

本研究中通过对Wang等［9］提出的HARS方案进行分析，发现该方案存在群成员改变攻击，并给出了攻击方法，继而对其方案加以改进，又对新方案进行了安全性分析，证明了改进后的方案更具有安全性。

［1］ Rivest R L，Shamir A，Tauman Y.How to leak a secret［C］//LNCS.In Advances in ASIACRYPT 2001，Berlin:Springer－ Verlag，2001，2248:552 －565.

［2］ Masayuki A，Miyako O，Koutarou S.1 － out－ of－ n signatures from a variety of keys［J］.IEICE Trans Fundamentals，2004，E87－A:131－140.

［3］ Zhang F G，Kwangjo K.ID －based blind signature and ring signature from pairings［C］//LNCS.In Advances in ASIACRYPT 2002.Berlin:Springer－ Verlag，2002，2501:548 －566.

［4］ Herranz J，Saez G.New identity － based ring signature schemes［C］//LNCS.ICICS 2004，Berlin:Springer－ Verlag，2004，3269:27－39.

［5］ Ateniese G，Burns R，Curtmola R，et al.Provable data possession at untrusted stores［J］.Proc.14th ACM Conference on Computer and Communications Security(CCS'07），2007，202(3）:598 －609.

［6］ Curtmola R，Khan O，Burns R，et al.MR － PPDP:multiple－ replica provable data possession［J］.Proc.28thIEEE International Conference on Distributed Computing Systems(ICDCS'08），2008，201(2）:411－420.

［7］ Erway C C，Kupcu A，Papamanthou C，et al.Dynamic provable data possession［J］.Proc.16th ACM Conference on Computer and Communications Security，2009，11(9）:213 －222.

［8］ Zhu Y，Wang H，Hu Z，et al.Efficient provable data possession for hybrid clouds［J］.Proc.17th ACM Conference on Computer and Communications Security，2010，10(4）:756 －758.

［9］ Wang B Y，Li B C，Hui L.Oruta:Privacy－ preserving public auditing for shared data inthe cloud［J］.IEEE Fifth International Conference on Cloud Computing，2012，46(1）:295 －302.

［10］ Boneh D，Franklin M.Identity－ based encryption from the weft pairing［C］//LNCS.Advances in Cryptology － Crypto 2001.Berlin:Springer－Verlag，2001，2139:213 －229.

［11］ Barceto P S L M，Kim H Y.Efficient algorithms for pairing －based cryptosystems［C］//LNCS.Advances in Crptology －Crypto'02.Berlin:Springer－ Verlag，2002，2442:354 －368.

［12］ Galbraith S，Harrison K，Soldera D.Implementing the Tate Pairing［C］//LNCS.ANTS 2002，Berlin:Springer－ Verlag，2002:324－337.

Cryptanalysis and improvement of a homomorphic authenticable ring signature scheme

GAO Xue － chen1，GUO Xian － jiu1，2
(1.College of Information Engineering，Dalian Ocean University，Dalian 116023，China;2.Key Laboratory of Ocean Information Technology of Liaoning Province，Dalian 116023，China）

The new homomorphic authenticable ring signature scheme is analyzed，and it is used in the public auditing for shared data in cloud computing and proposed by Wang et al in 2012.It is found that their scheme is susceptible to group－changing attack whose method is also given in this paper.In order to avoid the attack，the paper deals with improvement of their scheme and scheme's security.

ring signature;bilinear pairings;public auditing

P315.69

A

10.3969/J.ISSN.2095 －1388.2014.02.021

2095 －1388(2014）02 －0201 －04

2013－05－18

上海市重点实验室开放课题项目 (AGK2013005）

高雪辰 (1988－），男，硕士研究生。E－mail:214751193@qq.com

郭显久 (1963－），男，博士，教授。E－mail:gxj@dlou.edu.cn