海洋模式中垂直混合参数化方案介绍
汪雷,王彰贵,凌铁军,左金清
(1.北京大学物理学院,北京100871;2.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室,北京100081;3.中国气象局国家气候中心中国气象局气候研究开放实验室,北京100081)
海洋模式中垂直混合参数化方案介绍
汪雷1,2,王彰贵2,凌铁军2,左金清3
(1.北京大学物理学院,北京100871;2.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室,北京100081;3.中国气象局国家气候中心中国气象局气候研究开放实验室,北京100081)
介绍了海洋垂直混合过程参数化方案的发展,以及不同参数化方案在海洋模式中的应用情况。首先,介绍不同垂直混合参数化方案的物理问题、理论依据、数学表达和特征,并对不同参数化方案进行了比较。其次,针对中尺度涡、亚中尺度涡以及波浪、潮流混合参数化的最新研究进展进行了总结并对垂直混合参数化的未来发展提出了一些建议。
湍流闭合方案;中尺度涡混合;亚中尺度涡混合;波浪混合;潮流混合
1 引言
地球流体原始方程组通常描述了一定时空范围平均的流体运动行为。由于受到计算资源的限制,在数值计算中往往需要在更大的时空尺度上求解流体运动方程。更小尺度运动的效应,常以湍流通量散度形式出现[1],它们需要利用大尺度变量来参数化以闭合方程,这些过程常被称作次网格尺度物理过程。
海表混合层是海洋上层中直接与上覆大气、海冰相互作用的部分。一个完备的海表混合层参数化[2],必须模拟海风搅拌驱动的混合、不稳定浮力强迫、流切变不稳定、湍流平流、非局地混合,例如密集羽流渗入层流、重力内波破碎等物理过程。海洋内部温盐等属性沿位密面的传输主要通过大尺度洋流和中尺度涡来实现,而海洋内部跨密度混合发生在重力内波破碎区域[3],大部分波能量来源于海底反射的潮流、小尺度地形下重力波产生和辐射对地转运动的耗散、以及斜压不稳定的失稳。随着观测增多、模式发展和分辨率的提高,中尺度涡、亚中尺度涡以及波浪、潮流等过程对海洋混合的影响受到越来越多的关注。图1给出了海洋中小尺度混合过程的示意图。
海洋垂直混合是海洋混合中的重要部分,受到模式分辨率的限制,其在模式中需要进行参数化。海洋垂直混合参数化方案,根据混合系数的选取可分为:常混合系数、依赖Richardson数的方案和湍流动能模型等[1]。常混合系数方案,动量垂直粘性和示踪物垂直扩散系数在整个海洋设定为常数。由Richardson数决定的混合方案,利用观测资料寻找垂直湍流活动和大尺度海洋结构之间的联系,通过模型诊断出垂直混合系数与大尺度变量之间的关系。湍流闭合模型,则是一种基于湍流动能诊断方程和湍流特征长度闭合假设的模型。随着观测的增多和理论的发展,许多小尺度物理过程得到了更精确的刻画。
范植松[4]回顾了大洋内部、浅海内部混合的主要过程和一些参数化方法。近十年来,随着海洋模式的发展,国内外涌现出了一些新的海洋垂直混合参数化方案。本文将介绍影响重大的海洋垂直混合参数化方案、以及该领域最新的进展,并进行系统的总结与展望。
2 海洋垂直混合参数化方案
海洋模式旨在求解大尺度速度和温盐度的运动学方程,其中,动量、温盐通量是由速度、温盐扰动量的非线性相互作用所引起的。在局地湍流模型中,动量、温盐通量常表示为大尺度变量梯度的函数。模式分辨率通常大于切变不稳定、内波破碎等垂向湍流发生的主要源汇尺度,湍流运动一般未能显式求解,而是需要对其进行参数化处理。海洋上层的垂直混合过程是大气和海洋之间热量、水、动量交换的重要方式,下面我们将介绍一些具有代表性的垂直混合参数化方案。
2.1 KT67混合层模型(The Kraus-Turner mixed layer model)
研究对象:Kraus和Turner[5]考察了海表过程如辐射穿透、海表冷却和风搅拌所引起的层结过程。在盛夏,辐射穿透引起的对流混合与风搅拌作用具有相同的量级;在冬季,混合层厚度和稳定性主要由海表冷却控制,辐射穿透或风搅拌的作用相对较小。
理论依据:假定影响水柱的热量和机械能不受水平速度、平流或旋转的显著影响,而在海表附近向下穿透,Turner和Kraus[6]建立了一个简单的季节温跃层模型。在热量给定时,所有搅拌动能用于改变系统的位能,充分混合后得到表层混合厚度和温度。
表达形式:混合层是垂直均质水层,在假定外源、汇平衡后略去时间倾向项,得到湍流动能诊断方程,求解水层厚度。通过热量平衡以及动能平衡方程得到水层厚度[5]:
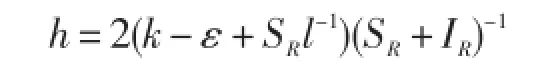
式中,k,ε,SR,IR,l分别与风输入动能、耗散、太阳辐射、红外辐射和长度尺度有关。
混合层底的厚度是模式预报量。在密度坐标系模式中,KT67混合层模式的混合层底与模式垂直坐标吻合,但卷出过程很难处理。
在混合坐标海洋模式如HYCOM[7]中,KT67混合层模式兼容的困难之处在于,需要记录混合层底的浮力变化以近似混合层夹卷对湍动能平衡的贡献,和热力、动力变量不连续以计算混合层夹卷对其影响。完整KT67方案,设计unmixing方案以减少混合层和海洋内部属性的数值交换。由于unmixing方案十分复杂,简化KT67方案通过松弛混合层底为预报量这一条件,在计算效率提高和数值误差增长之间权衡。
特征:KT67模型[5]仅仅控制表面混合层,使用时需同时加入考虑内部跨密度混合算法。HYCOM[8]提供了该参数化方案选项。
2.2 PWP86动力不稳定模型(Price-Weller-Pinkel dynamical instability model)
研究对象:海洋上层的热含量存在着众所周知的日循环,午后的温度、速度廓线表现出海表混合、分层剪切的上下两层结构。在海表加热和风应力已知时,预报海洋日循环的关键在于热量“陷阱”的确定。Price等[9]发展了一个对加热和风混合响应的上层海洋简单模式,以模拟日循环。
理论依据:在仅仅使用混合层夹卷时,整体混合层模式可给出合理的表面强迫,但对过渡层的模拟存在突变和偏浅的问题。在仅仅使用梯度混合时,模式对表面强迫的模拟也相对合理,只是无法模拟风驱动的海表混合层,加入自由对流过程后可得到改善。通过构造海表混合层,并且考虑混合层下的层流混合,可得到相当真实的廓线结构[9-10]。
表达形式:混合由三步完成:
(1)自由对流。海表热量损失出现静力不稳定时(∂zρ≥0),发生自由对流,对流混合至对流深度(日循环的典型值小于1 m);
(2)整体混合层夹卷。当整体Richardson数(Rib)小于临界值(0.65)时,混合层夹卷相邻下层,在新形成的混合层中使所有的变量均质,其中
(3)相邻层结垂直切变不稳定混合。若Richardson数(Ri)小于临界值(0.25)时,界面上下层混合,其中,Brunt-Väisälä频率,ρ为位密。在日循环中,后两种混合在垂直混合过程中占优势,由于Richardson数中出现的速度完全是由风驱动的,从这种意义上来说,可视为风-混合过程。
特征:PWP86方案[9]丢失了混合层特征,如对数廓线和非局地输送;在对流稳定条件下,该方案无法描述在混合层以下层结区由对流引起的额外夹带。PWP86方案提供了表面混合层以下的切变不稳定混合,未给出内波破碎等引起的背景混合。HYCOM[8]使用PWP86方案时,同时启动显式跨密度混合算法。
2.3 BL79方案(Bryan-Lewis water mass model)
研究对象:考察海洋环流在地球热平衡中的作用时发现,温跃层厚度对次网格尺度运动的参数化方案十分敏感,其中温跃层的平均厚度与全球有效位能成正比[11]。
理论依据:在地转条件下,即使闭合参数不同,有效位能和总动能也保持一个几乎恒定的比例。浮力强迫做功使动能转化为位能,浮力做功引起能量传输的方向取决于能量库的耗竭情况,即耗散、风做功供给和非均匀加热的差异[12]。温跃层厚度与参数变化之间有明确的格局,当参数改变使得风做功增加或者耗散减小时,海洋环流的总能量增加,这意味着密度层结更大的偏移和模式中更深的温跃层。
表达形式:温盐控制方程为:
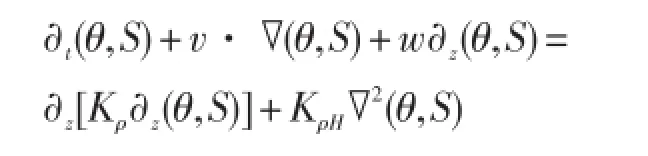
式中,水平粘性系数KmH和垂直粘性系数Km取为常数。水平扩散系数KρH是垂直坐标的函数KρH(z)=KρHB+(KρHS-KρHB)e-0.002z。垂直混合系数是稳定度的函数,不稳定时,系数无限大,不稳定水柱温盐彻底混合;稳定时取为垂直坐标的简单函数。垂直扩散系数Kρ在温跃层最小且随深度增加而增大,其计算方程考虑了风搅拌对上层海洋的作用:
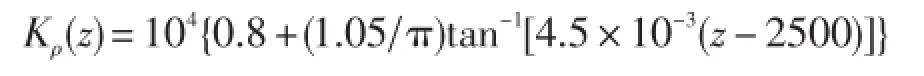
特征:在海洋环流数值模式尤其是气候模式中,通常采用BL79方案[11]来确定背景垂直湍扩散系数。该方案给出的垂直湍扩散系数只是深度z的函数。MOM[13]等加载了BL79方案。
2.4 PP81混合方案(Pacanowski-Philander mixing scheme)
研究对象:海表混合过程非常重要,KT67模型[5]考虑了风搅拌和跨混合层的夹带作用,但是忽略了海洋对风场变化的动力响应,故KT67模型在局地通量占主的区域效果不错。而在风场再分布效果大于局地作用的热带地区,KT67模型表现不佳。在热带海洋的上层,表面通量和对风场变化的动力响应都是重要的。
理论依据:观测表明,混合过程受到平均流剪切的强烈影响[14-15]。通过经验研究,Jones等人[16]给出了黏性/扩散系数与Richardson数的关系。PP81混合方案[17]主要应用在热带海洋,扩散系数依赖于Richardson数。由于该方案能够较合理地描述强垂直切变与黏性之间的关系,它可以更好地模拟赤道温跃层和赤道潜流。
表达形式:垂直扩散系数和粘性系数是Richardson数(Ri)的函数。式中,垂直粘性系数Km为:;垂直扩散系数Kρ为:背景值Kmb、Kρb由运行时间决定。在POP中,α=5,n=2。
特征:海洋混合过程极其复杂,PP81混合方案[17]只是简单地把垂直混合系数设为Richardson数的函数,而忽略了其它的混合过程,造成该方案在中高纬度的模拟结果不佳。由于湍流动能耗散率与Richardson数的关系随深度变化,PP81方案依赖于Richardson数的简单混合参数化方法并非对所有深度有效。采用该方案的模式有LICOM[18]、MOM[13]、NEMO[1]、POP[19]等。
2.5MY82湍流闭合方案(Mellor-Yamada Turbulence Closure Model)
研究对象:湍流粘性或混合长假说对二维湍流边界层有可观的预测能力。无压力梯度、热传输时,平均速度场闭合模型采用常数参数的平坦湍流层,无法预测层结效应。平均湍流场闭合模型由平均湍流能量模型和平均雷诺应力(MRS)模型组成时,虽然成功用于中性层,但是对于分层流MRS的计算量惊人。
理论依据:将湍流理论扩展到层结流体,Mellor[20]建立了湍流闭合模型。为了实现准确性和计算速度的优化,Mellor和Yamada[21]利用观测对湍流模型进行了简化。从四阶到二阶模型,求解的偏微分方程数量由十个降到两个,而结果十分相似。为便于其在三维大气和海洋模型中的应用,Mellor和Yamada[22]对三阶模型简化得到2.5层模型。
表达形式:温度扩散方程可写为:
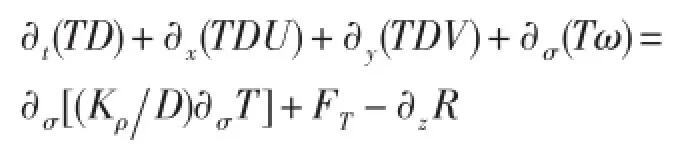
式中,粘性系数Km和扩散系数Kρ取决于湍流速度尺度q、特征长度l以及反映层结的Richardson数Ri[22]:
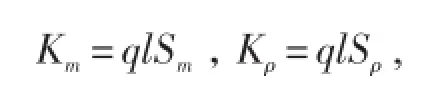
湍动能k和预报量kl,由下列方程控制:
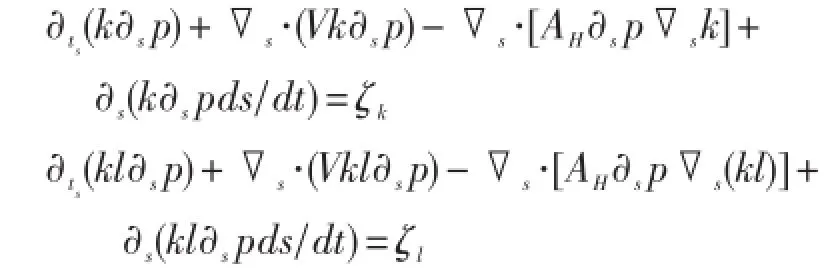
方程右端代表局地过程的作用。左侧第二至四项分别为水平平流、水平扩散、坐标转换时跨坐标引起的通量。温、盐项的局地作用表现为垂直扩散和海表强迫。湍动能和预报量的局地作用表现为边界层强迫、垂直扩散以及垂直切变产生、与位能的相互转化以及耗散。Sρ,Sm与Ri的有关:
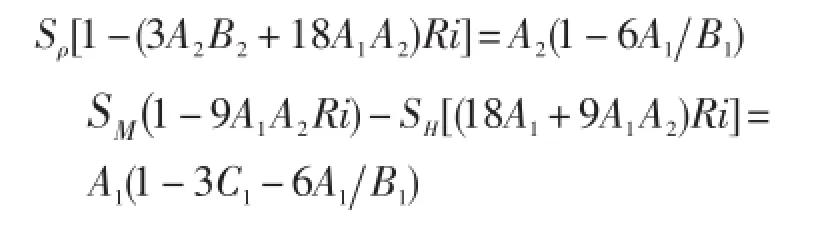
特征:MY82方案[20-22]产生从海表到海底的混合,弱混合发生在海洋内部,强混合产生在海表边界层,增强混合在洋底。该方案对混合层动力过程的模拟较好,但混合层厚度可能偏浅[23],在对流夹带偏弱、稳定密度梯度情况下混合偏小[24]。MY82方案的湍动能和预报量,在POM[25]中是垂直交界面变量,而在HYCOM[8]中是层变量。
2.6 GGL90湍流闭合方案(Gaspar-Grégoris-Lefevre TKE Turbulent Closure Scheme)
研究对象:对于那些垂直扩散系数为常系数或依赖Richardson数的简单参数化方案,上混合层模拟往往较差。简单整体模型如KT67[6]计算高效,但是仅适用于边界层。复杂的湍流闭合方案如MY82[21],提供了更加真实的垂直湍流混合,但在湍流主长度尺度的确定上存在不足。
理论依据:GGL90湍流闭合方案[26]是一种基于湍流动能诊断方程和湍流长度尺度闭合假设的参数化方案。Bougeault和Lacarrère[27]最早提出了简单、物理意义清晰的大气湍流闭合模型,Gaspar等[26]将其应用到海洋模式中,Madec等[28]对混合长度尺度的公式进行了改进。
表达形式:湍流动能的时间演变是垂直切变制造、层结破坏、垂直扩散和Kolmogorov耗散共同作用的结果[26]:
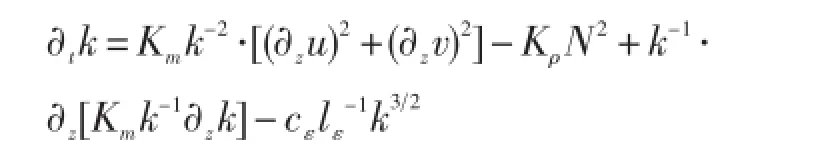
式中,海表湍动能由风应力场确定,当考虑表面波破碎时,使用较大的值。假设底层湍动能为紧邻上层湍动能的值。其中,垂直涡粘性和涡扩散系数分别为:
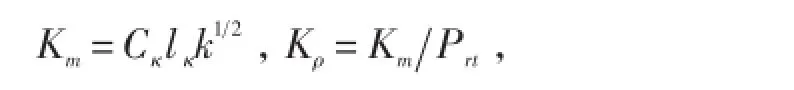
lε和lk分别为粘性、混合长度尺度,Prandtl数(Prt)依赖于局地Richardson数。简化的湍流长度尺度:,以到海表lu、海底ld、或局地垂直尺度因子为界,仅适用于层结稳定区域。针对局地层结不稳定,考虑长度尺度的垂直梯度项[28]:,即长度尺度的垂直变化不大于深度变化。
通过修正表面长度尺度和湍动能的数值以及海气拖曳系数来参数化表面波破碎能量效应[29-30]。 GGL90上边界条件为[29]:αCB是取决于“波龄”的常数。湍流长度尺度的上边界条件:,VC是von Karman常数,CC是Charnock常数。
特征:GGL90方案[26]指定了两种不同的特征尺度来分别表示混合和耗散,由于它们与所有深度的湍流长度相关,所以得到的混合参数化并不限于上边界层,而是可以应用在海洋整层。MITGCM[31]、NEMO[1]等模式采用了该参数化方案。
2.7 GISS01混合层模式(Goddard Institute for Space Studies)
研究对象:海洋混合过程的模拟通常采用单点湍流闭合模型,特别是MY82方案[22]开创了1980年代最先进的湍流模型。该方案使用了较小的临界Richardson数,且假定湍流不受旋转影响。随着湍流模型的发展,一些关键物理过程的模拟,如临界Richardson数取值、非局地分层和剪切、旋转、混合层下的混合等,都需要得到进一步的提高[32]。
理论依据:GISS01混合层模式根据实验观测来调整临界Richardson数(约为1),并通过求解动力系统三阶方程而得到包含分层和剪切作用的表达式。在混合层下的开洋面上考虑内波破碎等,地形附近则考虑潮耗散或地热加热作用。提出了雷诺应力模式的热、动量扩散系数表达式[32],并对双扩散过程[33]进行了完善。
表达形式:扩散系数Kρ(rρ,N,Ri,ε)取决于密度比rρ、Brunt-Väisälä频率N、Richardson数Ri和动能耗散率ε,其中下标ρ=(m,h,s)分别代表动量、热量和盐度,
密度比和Brunt-Väisälä频率由海洋环流模式的大尺度场计算得到。剪切作用由Richardson数表征,混合层内主要为风驱动的大尺度剪切,混合层之下则是小尺度剪切如内波为主。耗散率表示混合相关的物理过程,混合层内主要为风搅拌作用;在混合层下的开洋面上考虑内波破碎等,地形附近则考虑潮耗散或地热加热作用。GISS01方案适用于双稳定、双不稳定、盐指和对流扩散情况:
双稳定(∂zT>0,∂zS<0,rρ<0,RiT>0)
双不稳定(∂zT<0,∂zS>0,rρ>0,RiT<0)
盐指(∂zT>0,∂zS>0,rρ>0,RiT>0)
扩散对流(∂zT<0,∂zS<0,rρ>0,RiT>0)
特征:GISS01方案[32-33]适用于混合层及其以下的垂直混合参数化。该方案首先计算压力网格点上的粘性、扩散系数,随后使用隐式方案求解垂直扩散方程,并将粘性廓线水平插值到速度网格点,最后求解动量的垂直扩散方程。GISS01方案未对非局地效应进行参数化。HYCOM[8]加载了该参数化方案。
2.8 GLS03湍流闭合方案(Generic Length Scale scheme)
研究对象:海洋模式中雷诺-应力模型的应用在湍流长度尺度的选择上存在争议。所有雷诺-应力和两阶-方程模型都采用了经典串级模型:在物理上,使用(l,ε)中某变量并无客观优势,而在数学和计算上,模式性质受到长度尺度变量的很大影响。
理论依据:GLS03湍流闭合方案[34-35]包含两个预测方程:湍动能方程k和通用尺度ψ方程。通过适当的变换,GLS03方案可以复原一系列著名的湍流闭合方案,如MY82的k-kl方案[22]、Rodi的k-ε方案[36]和Wilcox的k-ω方案[37]等。
表达形式:湍动能由湍流传输Tk、切变产生GS、浮力制造GB和耗散项ε确定:
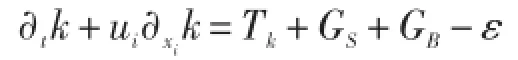
通用尺度lψ与湍动能和耗散相关lψ=~lψ(k,ε),方程可写为:
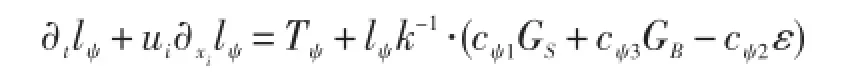
式中,Tψ为传输项,cψ1、cψ1和cψ1是模式常数。进一步假定lψ依赖于k和ε的乘积:,通过适当变换p、m和n的值,通用尺度方程可复原一系列著名的模型(见表1)。

表1 通用尺度中定义的p、n和m及其与著名二阶方程模型的关系[34]
在一定条件下,GLS03方程组可以化为[1]:
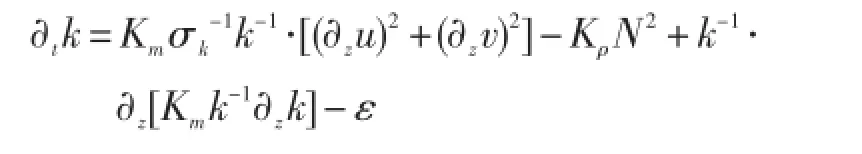
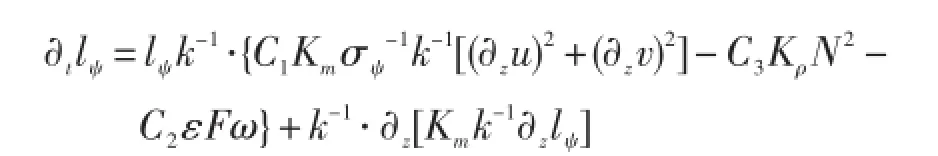
特征:GLS03方案[34-35]既可以用来分析已有模式,本身又可作为广义模式方程。对于制造等于耗散的传统标准流动情况,GLS03方案与传统模式表现相当。但对于无切变情形,耗散由湍流传输平衡的情况,此时除Wilcox的k-ω方案[37]外模拟效果都不好。传统模式对边界附近廓线的模拟存在困难。另外,GLS03方案解析解指出,模式参数间相互依赖很强。当合理使用这些参数时,模式在均质层结、切变流中表现良好。NEMO[1]等模式采用了该参数化方案。
2.9 KPP94参数化(K-Profile Parameterization)
研究对象:海洋垂直混合过程可分为海表边界层和海洋内部两种截然不同的混合型。通常使用的混合方案未考虑某些潜在重要的边界层物理过程,需要发展新的参数化方案代表这些物理过程。
理论依据:在海表边界层,KPP94方案对风驱动混合、表面浮力通量和对流不稳定进行参数化。在海表强迫下,边界层混合增强,这使得边界层属性渗透到温跃层。海洋内部混合由切变不稳定、背景内波破碎和双扩散控制。另外,该方案还对温、盐非局地混合作用进行了参数化,允许逆梯度通量的发展。
表达形式:KPP94方案[38-39]为半隐式,需要多步迭代过程。首先,在模式界面和网格上计算内部混合系数。其次,诊断出网格上的边界层深度。第三,计算网格上的边界层混合系数,代替初始值。最终得到网格上的平均系数。
海表通量:初始海表热力、动量通量在上层设为均匀分布[8]。
海表边界层厚度由整体Richardson数(Rib)确定。
垂直混合:通过水平平流、扩散、动量和通量方程得到每个网格点变量值,将垂直扩散视为海表、底边界上零通量的纯一维问题求解。
特征:非局地KPP 94方案[38-39]是非刚盖混合层模型,统一了垂直混合中的多种未解析过程[31],以处理海洋边界层、海洋内部的不同混合过程。KPP94方案有效地刻画了从海洋边界层到海洋内部混合系数减小的特点,可以应用在较粗网格和不平坦地形情况[8],在HYCOM[8]、MITGCM[31]、MOM[13]、NEMO[1]、POP[19]等模式中使用。
2.10 GM90中尺度涡参数化(Gent-McWilliams Parameterization)
研究对象:中尺度涡是涡旋场中最有活力的部分,支配着物质属性的等密度面混合。前人提出的涡扩散通量是沿等密度面的方向,而这不满足平均密度平衡。GM90方案[40]针对非涡分辨海洋环流模式,将次网格中尺度涡混合参数化,以描述中尺度涡对于大尺度位温、盐度及其它示踪物的影响。
理论依据:绝热和风驱动环流的精细数值解表明,平均速度导致的大尺度密度通量散度由中尺度涡诱发的密度通量散度平衡。GM90方案利用准绝热参数化的构想,在粗分辨率模式中保持平均示踪物浓度在等密度面上守恒。等密度层厚度沿等密度面进行混合,对示踪物附加平流和扩散项来实现中尺度涡对示踪物传输的参数化。将大尺度速度与涡诱发速度之和视为“有效速度”,得出与绝热模型相似的解[41]。
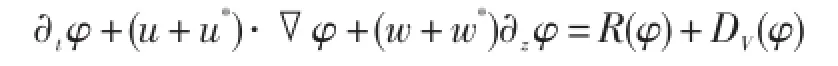
表达形式:示踪物传输方程为[19]:式中,中尺度涡诱发的推注速度:方程右侧第一项采用等中性扩散算子[42]:R(φ)=∇3(K·∇3φ),K代表沿等密度面扩散的对称张量。在POP模式中,将推注速度写为偏斜通量形式[43]:,B代表反对称张量。
传输方程可以重新写为:
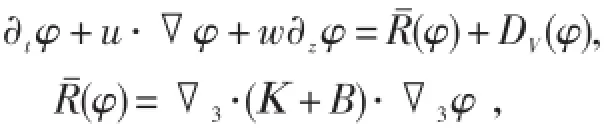
新公式对中性坡度的描述避免了非线性不稳定的激发。
在MITGCM中,涡参数化方案调用GM90方案前,首先使用Redi涡参数化方案[42],利用沿局地等熵面的扩散算子实现示踪物属性沿等熵面的混合。
特征:GM90方案[40]要求将背景扩散项中的水平扩散部分去掉,这是因为它有可能产生不适当的穿过等位密度面的扩散。对于次网格尺度的物理过程,GM90方案给定的侧向涡旋系数对大尺度度特征实际变化的反映并不理想,且未考虑跨密度混合。使用该方案的有LICOM[18]、MITGCM[31]、MOM[13]、NEMO[1]、POP[19]。
2.11 FKFH08亚中尺度涡参数化(Fox-Kemper-Ferrari-Hallberg restratification effects by submesoscale eddies)
研究对象:典型的海洋层化和切变允许两种斜压不稳定:贯穿整个深度的深厚中尺度不稳定,以及限于弱层结海表混合层的浅薄亚中尺度不稳定[44]。浅混合层不稳定是非地转斜压不稳定,以其快速增长率、小尺度区别于深厚中尺度不稳定,且前者在强混合事件后上层海洋的再层化中发挥重要作用。
理论依据:对于FKFH08方案[45-46],海洋混合层亚中尺度涡再层化效应发生的时间尺度远小于由中性物理参数化的中尺度涡。有限振幅斜压不稳定驱动了混合层的再层化,等密度面发生由垂直向水平的倾斜。参数化过程引入了翻转流函数,它正比于水平密度梯度、混合层深度平方和惯性周期的乘积。
表达形式:FKFH08参数化[45]是通过引入矢量流函数来实现:
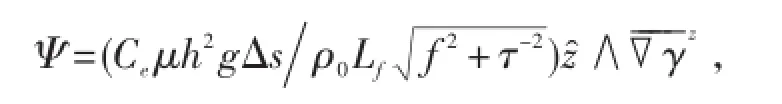
式中,Ce为无量纲数,μ混合层垂直结构函数,h混合层厚度,g重力加速度,Δs水平网格距,ρ0为 Boussinesq密度常数,Lf亚中尺度涡宽度尺度,f科氏力参数,τ亚中尺度涡的时间尺度,z=δ-d,d为海水深度,δ为自由海表偏差,是混合层平均参考位密水平梯度。写为分量形式:
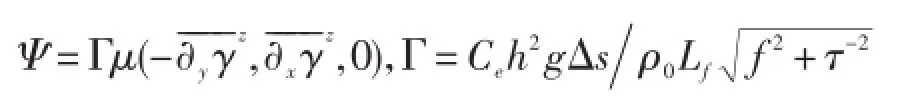
这些公式适用于混合层,利用水平浮力梯度进行参数化:-ρ0∇b=g∇γ=g(∂θγ∇θ+∂Sγ∇S),这与局地位密梯度有关。锋的尺度可以是常数,或通过斜压Rossby半径计算得到:混合层平均的浮力频率。
示踪物浓度受流函数的影响:
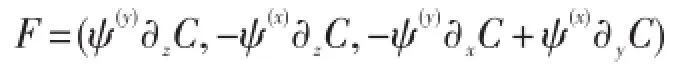
涡诱发速度表示为:
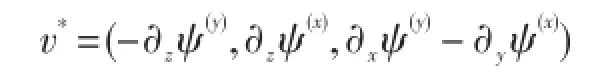
特征:在稳定层结情况下,FKFH08方案[45]的涡传输与GM90等[41]诱导速度传输不同。Fox-Kemper[47]等评估了FKFH08方案对全球海洋气候模拟的影响。MOM[13]加入了该方案,对近海表混合层层化的弱偏差有改善。风-锋、对流-锋相互作用和锋生过程等其它亚中尺度效应,目前尚未参数化。
2.12CB94波浪增强混合(Craig-Banner waveenhanced turbulence)
研究对象:在海洋表面,风将动量传输给海水。动量首先进入到表面波,通过波破碎传递给表面流场。相邻海面的湍动能随之增强,通过动量混合影响邻近海表的洋流廓线。海表波动的潜在影响包括:产生斯托克斯漂移和雷诺应力[48],影响平均流,以及波破碎时释放混合下传的湍动能。
理论依据:观测表明,表面几米的子层,湍流在海表波动作用下增强,该层的耗散率随深度以3—4.6幂数递减。CB94方案[29]将涡耗散表示为湍流速度和长度尺度的乘积,对波破碎的影响以海表能量源的形式进行参数化。在此波强化层,湍动能向下的通量由耗散平衡。
表达形式:湍动能方程为:
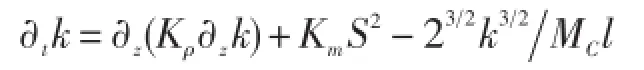
式中,k为湍动能,Kρ为湍流扩散系数,Km为湍流粘性系数,S2=(∂zu)2+(∂zv)2为切变产生项,l为长度尺度,MC为模式常数。Mellor和Blumberg[30]在以上方程右端加入浮力项作用-KHN2。
海表湍动能的边界条件为:
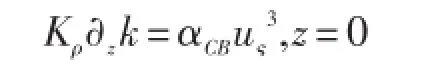
Mellor等[30]对湍动能闭合模型进行了调整,以包含表面波破碎能量的效应,校正作用于表面长度尺度、湍动能取值和海-气托曳系数。
特征:当混合层相对较浅时,使用CB94方案[29]对夏天海表温度虚高的偏差有改进。NEMO[1]等模式采用了该参数化方案。
2.13 QYY04波致混合方案(Qiao-Yuan-Yang waveinduced vertical viscosity)
研究对象:近海温度的垂直结构存在明显的季节变化。模式模拟的夏季海表温度通常偏高,上混合层偏浅,这可能是由上层混合强度不足导致的。波浪破碎在上层混合中发挥重要作用[29,49-50],然而海洋模式对其模拟能力尚待提高。
理论依据:基于波流耦合模型[51],假定波致混合项为波数谱的函数,得到波浪和潮流混合方案[52-53]。通过海浪的波数谱数值模式积分得到波浪方向谱,计算出随时空变化的波致垂直粘性系数,将它作为垂直混合的一部分叠加到不同的湍流混合模型中,引入波浪运动对环流速度、温度和盐度的混合作用。
表达形式:将速度、温度、盐度等物理量分解为平均和脉动两部分[52]:,其中脉动速度进一步分解为湍流部分和波致扰动:ui=uic+uiw。温盐扩散通量可表示为:
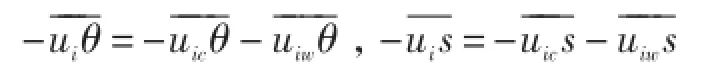
波致速度扰动可以用下式表示:
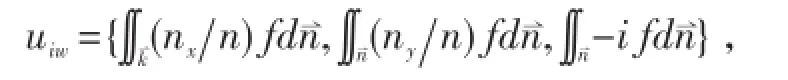
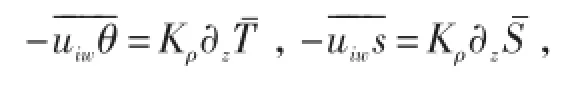
参数Kρ定义为波致垂直运动学粘性/扩散系数,依赖于混合长和波质点位移:
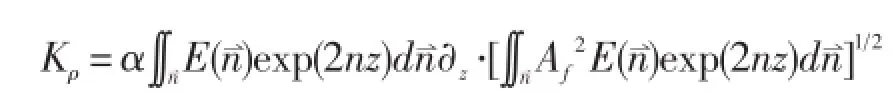
Kρ是决定波致混合的关键因子,应该考虑加入到海洋环流模式中。
特征:QYY04波致混合方案[52]对PP81和KPP94垂直混合方案均有显著提升,可减小太平洋冷舌偏冷和过于西伸的偏差,对海洋上层温度的模拟也有改善作用。
2.14 SJL04潮能耗散混合(Simmons-Jayne-LaurentMixingrelatedtotidalenergy dissipation)
研究对象:在层结海洋粗糙地形中,正压潮和潮流会诱发内波之间的动量交换。其中,重力内波破碎能量来自潮与粗糙海底地形作用时正压潮向内潮的能量散射;当潮流遇到大陆架时,发生底部拖曳摩擦。潮流模拟需要垂向几米、水平1—10 km的分辨率,在全球气候模式中难以实现,故有必要对其进行参数化处理。
理论依据:基于St Laurent等的理论[54],Simmons等[55]将dianeutral参数化方案引入海洋环流模式,假定混合发生在一单位Prandtl数,强化等量的dianeutral示踪扩散和动量粘性。当能量在小尺度耗散时,引起dianeutral混合。
表达形式:内潮破碎引起额外的垂直扩散项,表达为正压潮向斜压潮转换的能量E的函数[54]:
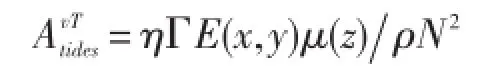
式中,η为潮耗散效率,典型取值为η=1/3,是局地耗散的部分内波能量通量,剩余部分作为低频内波模态贡献于背景内波场;Γ为混合效率,经常取值Γ=0.2。内波能量通量,ρ0为海水的参考密度,Nb是沿海床的浮力频率,(n,Am)为地形粗糙度的波数和振幅,u为正压潮速度,内波能量图谱通过潮流正压模型得出。描述湍流混合的垂直结构函数为:
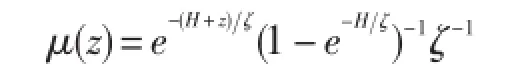
H为水柱总深度,ζ为湍流垂直耗散尺度。
海底拖曳引起的dianeutral扩散[13]可表示为:
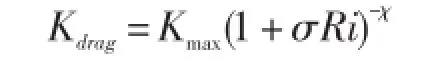
式中,σ和χ分别为无量纲参数。
特征:SJL04方案[55]显式给出了混合的潮能量,其混合系数随时空变化。相比水平/垂直系数均一方案,SJL04方案会显著降低温度、盐度模拟的偏差。MOM[13]和NEMO[1]都采用了该方案。
3 讨论与结论
本文通过对海洋垂直混合过程参数化方案的回顾,总结了常用参数化类型的理论依据、数学表达及应用情况等。
在模式混合层的设定上,海洋垂直混合参数化方案可分为整体混合模型和连续混合层模型两类[2]。整体模型假定海表边界层完全湍流,在混合层厚度中速度、示踪物分布均匀,如KT67方案[5]和PWP86方案[9]。结合KT67整体模型和PWP86模型中的梯度Richardson数判据,Chen等[56]提出了一种混合方案。由于整体方案无法分辨边界层中的垂直结构,不能计算非局地混合,故其性能受到限制。
连续混合可以较好的反映混合层细节特征。在BL79方案[11]中,垂直混合系数不随时间变化,仅为深度的简单函数。另外一些方案将垂直湍流混合与大尺度海洋结构相联系,例如,PP81方案[17]将这些系数规定为梯度Richardson数的函数。根据实验观测,GISS01模型[32-33]对Richardson数的取值进行了调整。值得注意的是,K理论在垂直混合方案中应用广泛,它将垂直混合参数化为涡扩散和涡粘性系数(K)与平均量垂直梯度的乘积。MY82方案[22]引入多阶预报方程求解不同湍流场,首先计算湍流混合长和速度尺度,然后确定垂直扩散和粘性系数。由于MY82方案[22]使用了相同的粘性和扩散长度尺度,GGL90方案[26]对其进行了改进,对粘性和扩散系数采用了不同的尺度。基于GLS03方案[34-35]的模拟结果表明,湍流长度尺度的选择存在约束条件,该方案既可用做广义长度尺度方案,还可以用来分析比较已有的模型。由于湍流混合模型计算较为复杂,KPP94方案[38-39]将大气模式常用的K-profile parameterization(KPP)[57]方案引入海洋模式,旨在建立一个包含所有重要过程的参数化方案,它在相对粗糙的垂直网格上运行良好。
随着观测、理论和数值方法的发展以及硬件条件的提高,对于海洋的模拟越来越精细化,海洋中小尺度过程如中尺度涡旋、内波等过程的参数化受到人们的关注。GM90中尺度涡参数化提高了大多数z坐标模式的物理完整性。另外,FKFH08亚中尺度涡参数化对海洋上层的层结模拟有明显改进。然而,目前中尺度涡、亚中尺度涡参数化仍然存在一些问题[3],例如海洋内部中尺度涡闭合与边界层方案的匹配问题、亚中尺度涡中的风-锋相互作用、能量串级在模式中尚未考虑。更精确的卫星海面观测对于中尺度涡的参数化过程有帮助。内波混合目前尚未有成熟的参数化方案,有待于进一步研究。
在海洋表面,波破碎对于动量由大气风场向海洋流场的传递具有重要作用。CB94和QYY04分别发展了波浪混合参数化方案,对海洋上层温度模拟的偏差有改善作用,并且加入QYY04方案还提高了PP81、KPP94参数化方案的性能。在海底地形作用下,正压潮流的能量向斜压潮流转化,增强海洋底层物理要素的混合。SJL04方案将潮流耗散加入到混合过程参数化,改善了温盐的模拟,对大洋深海层结的模拟有重要作用。在海洋垂直混合过程中,一些模式也考虑了双扩散[1,58],溢流[13]等过程的影响。
当前海洋垂直混合参数化方案众多,模式开发者一般选择偏好的参数化方案并直接编码进入模式。2014年在Breckenridge Colorado举行的海洋模式工作组/通用地球系统模式(OMWG/CESM)会议上,Levy等人[59]提出了通用海洋垂直混合(CVMix)的构想,目标是建立一种包含一系列参数化方案的易用程式库,最终实现参数化库的独立驱动。
随着数值计算的发展,国内外涌现出了一些新的海洋模式[60]。如MITGCM[31]采用了非静力框架,使其可以模拟多种尺度的流体现象,还使用了结构守恒映射,通过一种流体力学内核既可用于描述大气又可用于海洋。在今后的工作中,我们将对这些模式进行详细介绍。
致谢:论文的前期工作,受到与史珍博士共同调研工作的启发,作者深表感谢。
[1]Madec G.NEMO ocean engine[M].Note du Pole de modélisation, Institut Pierre-Simon Laplace(IPSL),France,2008,27:1288-1619.
[2]Griffies S M,Böning C,Bryan F O,et al.Developments in ocean climate modelling[J].Ocean Modelling,2000,2(3-4):123-192.
[3]Griffies S M,Adcroft A J,Banks H,et al.Problems and prospects inlarge-scaleoceancirculationmodels.In:ProceedingsofOceanObs'09:Sustained Ocean Observations and Information for Society[C].Venice,Italy,2010.
[4]范植松.海洋内部混合研究基础[M].北京:海洋出版社,2002.
[5]Kraus E B,Turner J S.A one-dimensional model of the seasonal thermocline II.The general theory and its consequences[J].Tellus, 1967,19(1):98-106.
[6]Turner J S,Kraus E B.A one-dimensional model of the seasonal thermocline I.A laboratory experiment and its interpretation[J]. Tellus,1967,19(1):88-97.
[7]Wallcraft A,Metzger E,Carroll S.Software Design Description for the HYbrid Coordinate Ocean Model(HYCOM),Version 2.2[Z]. DTIC Document,2009.
[8]Bleck R.An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates[J].Ocean Modelling,2002,4(1): 55-88.
[9]Price J F,Weller R A,Pinkel R.Diurnal cycling:Observations and models of the upper ocean response to diurnal heating,cooling,and windmixing[J].JournalofGeophysicalResearch:Oceans (1978-2012),1986,91(C7):8411-8427.
[10]Price J F,Mooers C N K,Van Leer J C.Observation and simulation of storm-induced mixed-layer deepening[J].Journal of Physical Oceanography,1978,8(4):582-599.
[11]Bryan K,Lewis L J.A water mass model of the world ocean[J]. Journal of Geophysical Research:Oceans(1978-2012),1979,84 (C5):2503-2517.
[12]Holland W.Energetics of barcoclinic oceans.In:Numerical Models of Ocean Circulation:Proceedings of a Symposium[C]. Washington,DC:NationalAcademy of Sciences,1975.
[13]Griffies S M.Elements of mom4p1[R].GFDL Ocean Group Techical Report 6,2010:444.
[14]Crawford W R,Osborn T R.Microstructure measurements in the AtlanticequatorialundercurrentduringGATE[J].Deep-Sea Research,1979,26:285-308.
[15]Osborn T R,Bilodeau L E.Temperature microstructure in the equatorial Atlantic[J].Journal of Physical Oceanography,1980,10 (1):66-82.
[16]Jones J H.Vertical mixing in the Equatorial Undercurrent[J]. Journal of Physical Oceanography,1973,3(3):286-296.
[17]Pacanowski R C,Philander S G H.Parameterization of vertical mixing in numerical models of tropical oceans[J].Journal of Physical Oceanography,1981,11(11):1443-1451.
[18]刘海龙,俞永强,李薇,等.LASG/IAP气候系统海洋模式(LICOM1.0)参考手册[M].北京:科学出版社,2004.
[19]Smith R,Gent P.Reference manual for the Parallel Ocean Program(POP),ocean component of the Community Climate System Model(CCSM2.0 and 3.0)[R].Technical Report LA-UR-02-2484,Los Alamos National Laboratory,Los Alamos, NM,2002.
[20]Mellor G L.Analytic prediction of the properties of stratified planetary surface layers[J].Journal of the Atmospheric Sciences, 1973,30(6):1061-1069.
[21]Mellor G L,Yamada T.A hierarchy of turbulence closure models for planetary boundary layers[J].Journal of the Atmospheric Sciences,1974,31(7):1791-1806.
[22]Mellor G L,Yamada T.Development of a turbulence closure model for geophysical fluid problems[J].Reviews of Geophysics, 1982,20(4):851-875.
[23]Martin P J.Simulation of the mixed layer at OWS November and Papa with several models[J].Journal of Geophysical Research: Oceans(1978-2012),1985,90(C1):903-916.
[24]Kantha L H,Clayson C A.An improved mixed layer model for geophysical applications[J].Journal of Geophysical Research: Oceans(1978-2012),1994,99(C12):25235-25266.
[25]Mellor G L.User's guide for a three-dimensional,primitive equation,numerical ocean model[M].Princeton,NJ:Atmospheric and Oceanic Sciences Program,Princeton University,1998.
[26]Gaspar P,Grégoris Y,Lefevre J M.A simple eddy kinetic energy model for simulations of the oceanic vertical mixing:Tests at station Papa and Long-Term Upper Ocean Study site[J].Journal of Geophysical Research:Oceans(1978-2012),1990,95(C9): 16179-16193.
[27]Bougeault P,Lacarrere P.Parameterization of Orography-Induced Turbulence in a Mesobeta--Scale Model[J].Monthly Weather Review,1989,117(8):1872-1890.
[28]Madec G,Delecluse P,Imbard M,et al.OPA 8.1,ocean general circulationmodelreferencemanual[M].NoteduPôlede modélisation,Institut Pierre-Simon Laplace,1998,11:97.
[29]Craig P D,Banner M L.Modeling wave-enhanced turbulence in the ocean surface layer[J].Journal of Physical Oceanography, 1994,24(12):2546-2559.
[30]Mellor G,Blumberg A.Wave breaking and ocean surface layer thermal response[J].Journal of Physical Oceanography,2004,34 (3):693-698.
[31]Adcroft A,Campin J M,Dutkiewicz S,et al.MITgcm user manual [M].MIT Department of EAPS,Cambridge,2008.
[32]Canuto V M,Howard A,Cheng Y,et al.Ocean Turbulence.Part I: One-PointClosureModel-MomentumandHeatVertical Diffusivities[J].Journal of Physical Oceanography,2001,31(6): 1413-1426.
[33]Canuto V M,Howard A,Cheng Y,et al.Ocean turbulence.Part II: Vertical diffusivities of momentum,heat,salt,mass,and passive scalars[J].JournalofPhysicalOceanography,2002,32(1): 240-264.
[34]Umlauf L,Burchard H.A generic length-scale equation for geophysical turbulence models[J].Journal of Marine Research, 2003,61(2):235-265.
[35]Umlauf L,Burchard H.Second-order turbulence closure models for geophysical boundary layers.A review of recent work[J].Continental Shelf Research,2005,25(7-8):795-827.
[36]Rodi W.Examples of calculation methods for flow and mixing in stratified fluids[J].Journal of Geophysical Research:Oceans (1978–2012),1987,92(C5):5305-5328.
[37]Wilcox D C.Reassessment of the scale-determining equation for advanced turbulence models[J].AIAA Journal,1988,26(11): 1299-1310.
[38]Large W G,McWilliams J C,Doney S C.Oceanic vertical mixing:A review and a model with a nonlocal boundary layer parameterization[J].ReviewsofGeophysics,1994,32(4): 363-403.
[39]Large W G,Danabasoglu G,Doney S C,et al.Sensitivity to surface forcing and boundary layer mixing in a global ocean model:Annual-meanclimatology[J].JournalofPhysical Oceanography,1997,27(11):2418-2447.
[40]Gent P R,Mcwilliams J C.Isopycnal mixing in ocean circulation models[J].Journal of Physical Oceanography,1990,20(1): 150-155.
[41]Gent P R,Willebrand J,McDougall T J,et al.Parameterizing eddy-induced tracer transports in ocean circulation models[J]. Journal of Physical Oceanography,1995,25(4):463-474.
[42]Redi M H.Oceanic isopycnal mixing by coordinate rotation[J]. Journal of Physical Oceanography,1982,12(10):1154-1158.
[43]Griffies S M.The gent-mcWilliams skew flux[J].Journal of Physical Oceanography,1998,28(5):831-841.
[44]Boccaletti G,Ferrari R,Fox-Kemper B.Mixed layer instabilities and restratification[J].Journal of Physical Oceanography,2007,37 (9):2228-2250.
[45]Fox-Kemper B,Ferrari R,Hallberg R.Parameterization of mixed layer eddies.Part I:Theory and diagnosis[J].Journal of Physical Oceanography,2008,38(6):1145-1165.
[46]Fox-Kemper B,Ferrari R.Parameterization of mixed layer eddies. Part II:Prognosis and impact[J].Journal of Physical Oceanography,2008,38(6):1166-1179.
[47]Fox-Kemper B,Danabasoglu G,Ferrari R,et al.Parameterization of mixed layer eddies.III:Implementation and impact in global ocean climate simulations[J].Ocean Modelling,2011,39(1-2): 61-78.
[48]Phillips O M.The dynamics of the upper ocean[M].Cambridge: Cambridge University Press,1977.
[49]Mellor G L.One-dimensional,ocean surface layer modeling:A problem and a solution[J].Journal of Physical Oceanography, 2001,31(3):790-809.
[50]Mellor G.The three-dimensional current and surface wave equations[J].Journal of Physical Oceanography,2003,33(9): 1978-1989.
[51]Yuan Y,Qiao F,Hua F,et al.The development of a coastal circulationnumericalmodel:1.Wave-inducedmixingand wave-current interaction[J].Journal of Hydrodynamics,Ser.A, 1999,14:1-8.
[52]Qiao F L,Yuan Y,Yang Y Z,et al.Wave-induced mixing in the upper ocean:Distribution and application to a global ocean circulation model[J].Geophysical Research Letters,2004,31(11).
[53]乔方利,马建,夏长水,等.波浪和潮流混合对黄海、东海夏季温度垂直结构的影响研究[J].自然科学进展,2004,14(12):1434-1441.
[54]St Laurent L C,Simmons H L,Jayne S R.Estimating tidally driven mixing in the deep ocean[J].Geophysical Research Letters,2002,29(23):21-1-21-4.
[55]Simmons H L,Jayne S R,St Laurent L C,et al.Tidally driven mixing in a numerical model of the ocean general circulation[J]. Ocean Modelling,2004,6(3-4):245-263.
[56]Chen D,Rothstein L M,Busalacchi A J.A hybrid vertical mixing scheme and its application to tropical ocean models[J].Journal of Physical Oceanography,1994,24(10):2156-2179.
[57]Holtslag A A M,Boville B A.Local versus nonlocal boundarylayer diffusion in a global climate model[J].Journal of Climate, 1993,6(10):1825-1842.
[58]Merryfield W J,Holloway G,Gargett A E.A global ocean model with double-diffusive mixing[J].Journal of Physical Oceanography,1999,29(6):1124-1142.
[59]Levy M,Danabasoglu G,Griffies S,et al.Community Ocean Vertical Mixing(CVMix)Status Update[Z].OMWG Meeting. Breckenridge,CO,2014.
[60]郑沛楠,宋军,张芳苒,等.常用海洋数值模式简介[J].海洋预报,2008,25(4):108-120.
Review of vertical mixing parameterization in ocean climate modeling
WANG Lei1,2,WANG Zhang-gui2,LING Tie-jun2,ZUO Jin-qing3
(1.School of Physics,Peking University,Beijing 100871 China;2.Key Laboratory of Research on Marine Hazards Forecasting,NMEFC,Beijing 100081 China;3.Laboratory for Climate Studies,National Climate Center,China Meteorological Administration,Beijing 100081 China)
In ocean climate models,the parameterization schemes of vertical mixing processes are introduced. Firstly,the corresponding physical issues,theoretical basis,numerical expressions and characteristics of various vertical mixing parameterization schemes are introduced,and the evolutions of different schemes are shown. Secondly,the latest advancement about vertical mixing parameterization,owing to considering the contribution from the mesoscale eddies,submesoscale eddies,wave and tidal are summarized.Finally,we propose some suggestions on the future development in vertical mixing models.
turbulence closure scheme;mesoscale eddies mixing;submesoscale eddies mixing;wave induced mixing;tidal induced mixing
P731
:A
:1003-0239(2014)05-0093-12
10.11737/j.issn.1003-0239.2014.05.015
2014-06-02
国家重点基础研究发展计划(2010CB950303);国家自然科学基金(41376016,41205058);国家重点基础研究发展计划(2014CB745004)
汪雷(1984-),男,助理研究员,主要从事扰动位能、季风、海洋模式研究。E-mail:wangl@nmefc.gov.cn

