光源最优可行区自动选取算法在生物发光断层成像中的应用

张 倩，陈春晓，刘 高，阚星星，李婷婷

南京航空航天大学生物医学工程系，南京市，210016

光源最优可行区自动选取算法在生物发光断层成像中的应用

【作者】张 倩，陈春晓，刘 高，阚星星，李婷婷

南京航空航天大学生物医学工程系，南京市，210016

目的 提出一种最优可行区的自动选取方法，以降低生物发光断层成像光源重建过程中的病态性和欠定性问题。方法 根据光子传播模型将CCD获得的二维图像映射为体表光辐照度；利用有限元法求解光源与体内光强分布的关系矩阵；利用该文提出的最佳可行区自动选取方法确定光源可行区，并用吉洪诺夫正则化方法重建光源。结果 最优可行区中心点与真实光源中心点距离为1.26 mm，重建光源中心点误差为0.45 mm，体积误差为9.13 mm3。结论 该文提出的光源最佳可行区选取策略可有效地将可行区定位到真实光源附近，减少因主观定位可行区带来的重建误差，为获得高精度的光源重建结果提供保障。

生物发光断层成像；可行区；前向问题；逆向问题

0 引言

生物发光断层成像因其可连续检测、无辐射、成本低等优势成为近年来分子成像方法中的一个热点。这种成像技术是利用高灵敏度的CCD相机捕捉生物体表的微弱光子以重建体内光源的位置和大小，能够动态监控活体生物体内肿瘤的生长与转移、感染性疾病的发展、特定基因的表达等生物学过程，其在生命科学和药物开发等方面的研究具有极大潜力[1-3]。

生物发光断层成像通常包括前向问题、映射问题和逆向问题求解三部分。前向与映射问题是基础，逆向重建是核心。前向问题是根据已知的生物体组织器官的解剖结构、各组织器官的光学参数求得光在生物体内辐照度分布和光源的能量密度分布之间的关系矩阵[4-5]。映射问题是根据拍摄的生物体表的二维灰度图像，利用灰度与光强的线性关系将灰度值转换为光强值，然后映射为生物体表的光辐照度分布[6-7]。逆向问题是根据已知的关系矩阵与体表光辐照度分布对光源位置和大小进行重建，由于CCD拍摄只能获得生物体体表的光辐照度分布，缺少体内的数据，所以逆向重建问题是一个典型的病态性问题。Wang G等[8]在生物发光断层成像系统研究中提出了光源唯一性理论和逆向问题的病态性问题。Wang G等[9]在研究中还发现，利用组织解剖结构及其光学参数等先验信息能够有效降低逆向重建的病态性，并通过设定光源可行区，建立体表测量值与光源之间的线性对应关系，采用改进牛顿法和边界约束优化方法求解最小化问题，可以实现体内光源的重建。Lv Y等[10]提出了多级自适应有限元的方法，根据后验误差重新进行网格划分，从而降低了方程的欠定性。Jiang M等[11]采用迭代的EM算法和约束Landweber法对CCD采集的表面部分数据对光源进行了重建，并验证光源的约束条件对于重建结果的影响。He X等[12]使用截断最小二乘法，将系统误差与测量噪声都考虑在内，并采用改进广义交叉检验法进行光源重建，最后利用不同等级的噪声和物理实验证明了重建算法的有效性。Yu J等[13]提出了一种基于AFEM的全局算法，对目标周围网格进行细化，而其他区域则提供粗化网格，并考虑了不同离散化水平的方差。由于生物发光断层成像逆问题自身的病态性，因此，对于先验信息，尤其是可行区的设置尤其重要。通过设置合适大小的可行区，可以有效的降低逆问题的病态性。而现有的可行区设置方法中，多为根据生物体内光源的大概位置自行设置，而可行区的大小也是根据经验获得。因此，研究合理准确的可行区设置方法十分必要。

本文提出了一种根据后验信息自动选取最佳可行区的策略，确保了可行区位置的正确性，并尽可能缩小可行区大小，以降低逆问题的病态性。为了验证算法的正确性，课题组设计了仿体实验进行实验验证。用科学级CCD相机采集仿体八个角度的发光图片，并映射为体表光强；利用有限元方法求取关系矩阵，并根据本文提出的最佳可行区自动选取方法，确定可行区的范围；最后采用吉洪诺夫正则化方法对光源进行重建。

1 光子传输模型

在生物发光断层成像系统中，光子的传输路径包括两部分，即光子从生物体内部到体表面的传输及光子从生物体表面经由镜头透镜组到CCD探测器表面的传输。

1.1 光子在组织体内的传输模型

光子在仿体或生物体内部的传输过程可以用辐射传输方程(Radiative Transfer Equation，RTE)来精确描述。辐射传输方程以能量守恒定律为基础，考虑光子在不同介质传播时的吸收、散射等过程[14]。但是，辐射传输方程较为复杂，直接求解难度较大，而在600～900 nm波段内，生物组织对光子主要起散射作用，可对辐射传输方程进行一阶球谐波近似，得到扩散近似方程。稳态条件下的扩散近似方程表示如下[15]：

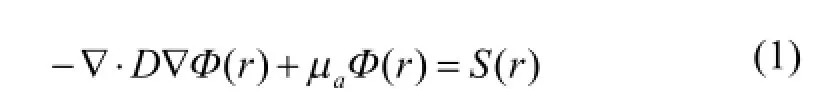
其中，D为与组织各向异性系数g、组织吸收系数μa、组织散射系数μs相关的量，表示如下：

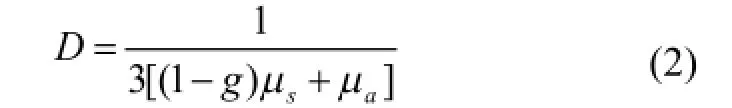
本文对扩散方程的求解采用了有限元方法，将生物体或仿体离散为许多四面体单元组成的网格，离散后的（1）式可表示为：

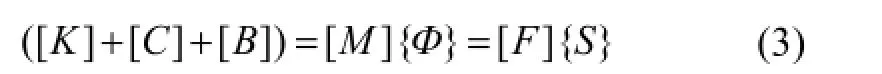
其中，K、C、B、M、F是对称稀疏矩阵，表示如下[9]：

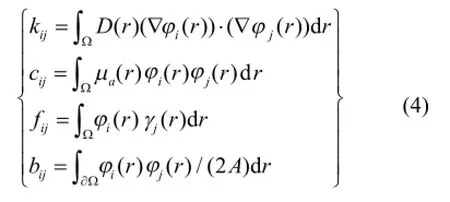
(4) 式中，Ω代表整个区域；i, j为网格节点索引；φ为整个区域的插值函数；γ为光源区域的插值函数。本文中的插值函数采用的是线性插值。

1.2 光在空气与透镜中的传播

光在空气及透镜中的传播可以简化为小孔成像模型来描述。如图1所示，光子从体表逸出后会向很多方向传播，但只有r方向的光子能够穿过凸透镜，到达相机的探测平面。根据朗伯余弦定律，面元dE发出的光传输到面元dR上的强度为：

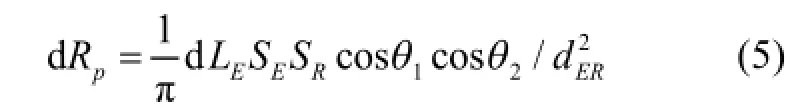
其中，dLE是面元dE的光辐照度，单位为W/m2；θ1和θ2如图1中所标记；SE是面元dE的面积；SR是面元dR的面积；dER是两个面元之间的距离。

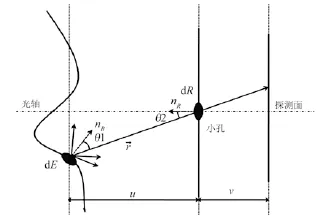
图1 光在空气与透镜中的传播Fig.1 Light propagation in air and the lens

在实际计算中，根据CCD的成像原理，像素点的灰度值与到达该像素点的光强是成线性关系的，线性关系表示如下：

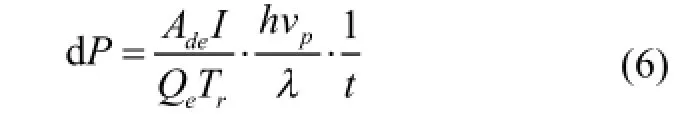
dP为到达像素点的光强；Ade为CCD相机的增益值，即转化为一个灰度值的电子个数；I为该像素点的灰度值；Qe为相机的量子效率；Tr为镜头透过率；h为普朗克常数；vp是光的传播速度；λ为光的波长；t为曝光时间。

根据(5)式和(6)式，可以将拍摄得到的多角度二维图片映射为三维体表的光辐照度分布，用于进行光源重建。

2 基于最佳可行区自动选取的光源重建

2.1 逆问题求解

根据1.1节中(3)式提到的体内辐照度分布和光源的能量密度分布之间的关系矩阵，可以变换得到(7)式：

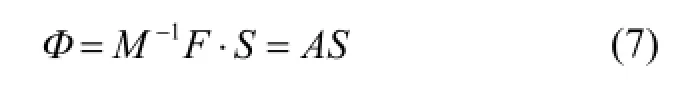
而在实际实验中，只能获取体表部分的光辐照度，却不能获取体内的，也就是说，Φ只有部分已知，这就造成了逆向问题的病态性。为降低逆问题的病态性，学者们多采用划定光源可行区的方法[16]，即假定部分区域为光源区域，而其余区域为非光源区域，赋值为零。这样一来，Φ和S都被划分为两块，根据Φ的已知区域对系数矩阵A进行行抽取，根据S的已知区域对系数矩阵A进行列抽取，则(7)式转化为如下：

此时，可将上式转化为最小二乘问题进行求解：

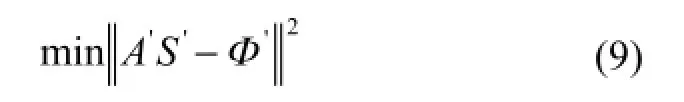
其中2为二范数。本文采用吉洪诺夫正则化方法对该最小二乘问题进行求解，并采用广义交叉检验法选取吉洪诺夫正则化参数。

2.2 最佳可行区自动选取

为了得到稳定并且准确的重建结果，通常需要足够的先验知识。因光源可行性区能够限定体内光源的分布区域，减少生物组织内的未知量，提高重建光源的唯一性和准确性则常常当作一种重要的先验信息。但由于缺乏对生物体内发光源的直观了解，导致光源可行性区的选取有着很大的随机性及不确定性，并且在传统的光源可行性区选取方法中人为干涉太多，难以实现自动及最优化选取。研究合理准确的可行区设置方法十分必要。本文利用重建光源有趋近于真实光源的特性，提出了自适应最优可行区自动选取的方法，其流程如图2所示。

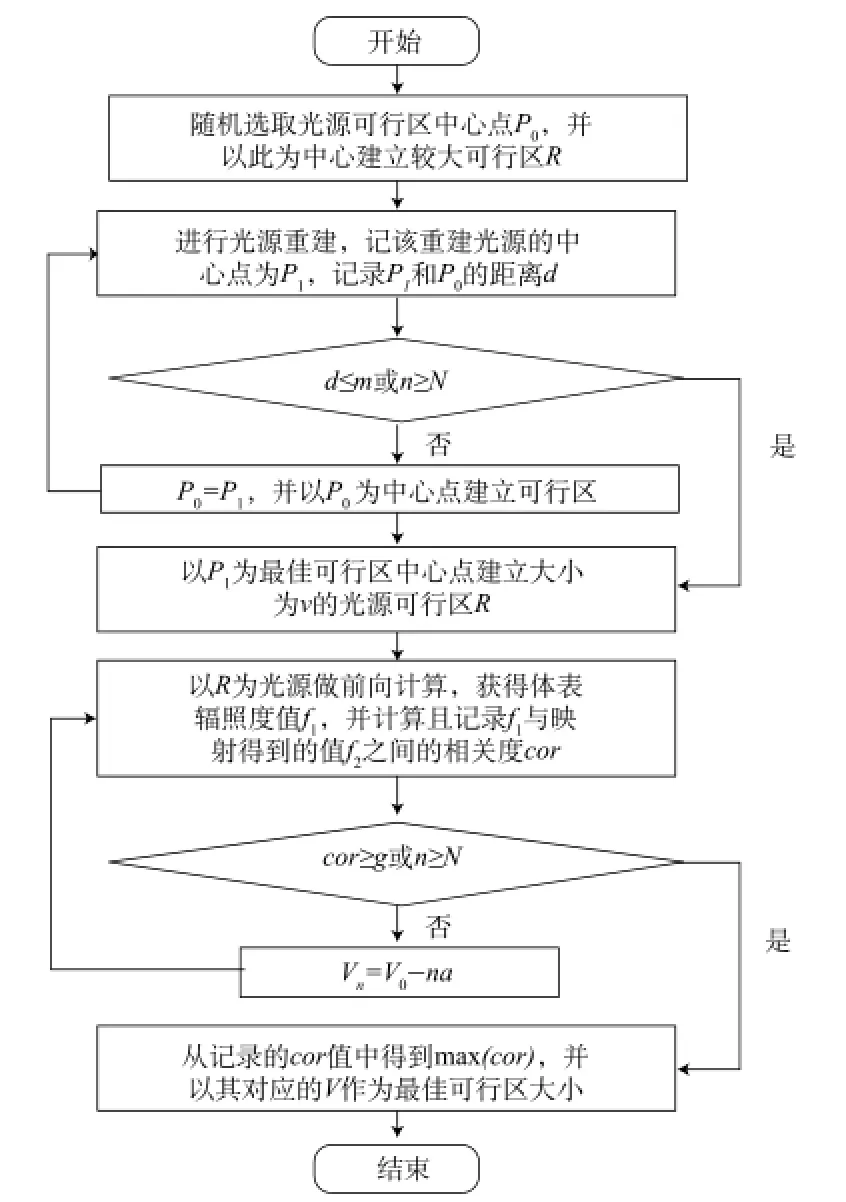
图2 最佳可行区选取流程图Fig.2 The fow chart of optimal feasible region selection

该方法的核心思想是对于任意给定的一个初始可行区，经过一定次数的迭代，能够确定一个与真实光源接近的点作为最佳光源可行性区中心点。根据中心点的位置，自动设置光源可行性区为模拟光源，计算前向方程，并与真实测量的表面光强值进行相关性的比较，选取相关度最高的结果便可确定最佳可行区的大小。具体实施步骤如下：

步骤1：在生物体内任意选取一个光源可行性区R，其中心点为点P0；

步骤2：利用生物自发光断层成像重建算法对生物自发光断层成像进行求解，得到一个重建光源，设该重建光源的中心为点R1；

步骤3：计算重建光源的中心点P1与光源可行性区中心点P0的几何距离d，若该几何距离d小于设定阈值μ(的取值可以根据重建算法精度设定，一般取值范围为0＜ μ ＜0.8 mm)或循环次数大于N，则以P1点为最佳光源可行性区中心，算法结束；若该几何距离d大于或等于设定阈值且循环次数小于N，则以P1点取代P0点重新设定光源可行性区R，循环次数加1，返回步骤2；

步骤4：利用步骤3确定的光源可行性区中心点，设立一个初始光源可行性区R；

步骤5：以可行性区为光源，利用生物发光断层成像前向公式计算生物体表幅照度值 f1，并与映射得到的幅照度值比较，求其相关系数cor的值；

步骤6：对步骤5求得的相关系数进行判断，若相关系数的值小于设定的阈值γ(0.9＜γ≤1)，且迭代次数小于最大迭代次数，则收缩光源可行性区大小，并转到步骤5；若相关系数cor的值大于设定阈值，或者是迭代次数达到设定的最大次数，则停止迭代，并从记录中的相关cor系数中选取一个最大的值，同时以其对应的光源可行性区大小作为最佳可行性区大小。

3 实验与结果

为证明本文所述算法的准确性，课题组利用仿体实验来进行算法验证。仿体三视图及网格如图3所示，其中真实光源中心点坐标为(0, 10, 22.5)。仿体由尼龙制作，尼龙的吸收系数和约化散射系数分别为0.013 8 mm-1和0.91 mm-1。仿体内光源采用红色荧光棒内的荧光溶液，荧光波长为600～780 nm，波峰为650 nm，室温下的发光强度为60 nW/mm3[17]。实验系统包含一台科学级CCD相机(Princeton Instruments exclusive PIXIS: 1024B_eXcelon)，一个微距镜头(TAMRON M118FM25)，一个光学暗箱，一个平移旋转台以及多枚滤波片。

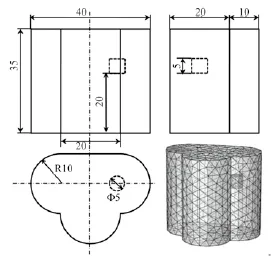
图3 不规则曲面柱体三视图及网格Fig.3 Three views and the volume mesh of the irregularity cylinder phantom

采集仿体8个角度的发光图像后，利用前面所提到的方法将二维灰度图像映射为三维体表面的辐照度。根据2.2节中所述的最佳可行区选取策略，设置初始可行区中心点为（5, 5, 10），初始可行区为边长10 mm的正方体。迭代过程图如图4所示，其中星形点为真实光源中心点。从图4可以看出，尽管初始可行区中心点距离真实光源中心点较远(14.36 mm)，但经过多次迭代后，可行区中心点已十分靠近真实光源中心点，两者距离仅有1.26 mm。图5记录了每次更新的可行区中心点距离真实光源点的距离，该距离逐渐变小，最终趋于稳定。根据本文提出的方法，最终获取的可行区中心点位置为(0.36, 11.16, 22.18)，与真实光源中心点距离为1.26 mm，可行区边长为7.5 mm。

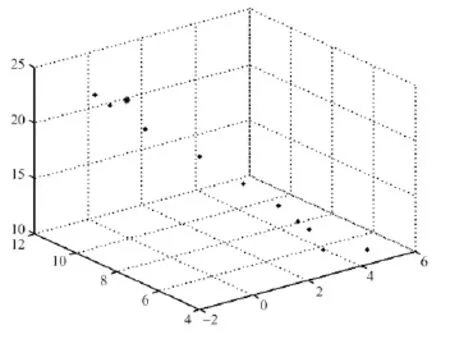
图4 最佳可行区中心点迭代图Fig.4 Iteration fgure of optimal feasible region centre

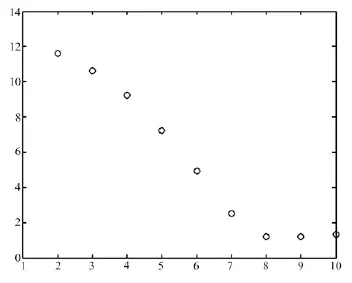
图5 可行区中心点与真实光源的距离Fig.5 Distance between feasible region centre and true source centre

根据上述获得的最佳可行区按2.1所述方法进行光源重建，真实光源的位置与形状如图6所示，重建结果如图7所示。可以看出，真实光源与重建光源的形状大小较类似，且位置几乎一致。真实光源的体积为95.20 mm3，重建光源的体积为86.07 mm3，误差为9.13 mm3。真实光源坐标为（0.00, 10.00, 22.50），重建光源中心点为(0.23, 10.25, 22.21)，两者的距离为0.45 mm。

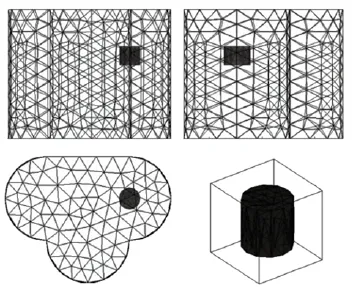
图6 真实光源三视图Fig.6 Three views of true source

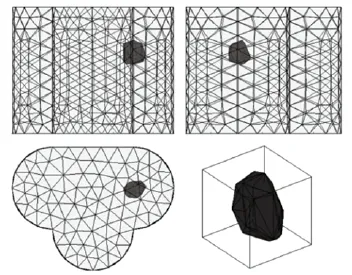
图7 重建光源三视图Fig.7 Three views of reconstructed source

4 结论

本文提出了一种用于生物发光断层成像中最佳光源可行区自动选取的方法，并利用仿体实验验证了该方法的有效性。实验表明，本文提出的可行区自动选取方法能够有效定位到真实光源附近，降低逆向重建的病态性和欠定性，为获得高精度的光源重建结果提供保障。

[1] Wang G, Cong W, Durairaj K, et al. In vivo mouse studies with bioluminescence tomography[J]. Opt Express, 2006, 14(17): 7801-7809.

[2] Wang G, Cong W, Shen H, et al. Overview of bioluminescence tomography-a new molecular imaging modality[J]. Front Biosci, 2008, 13(1281 -1293): 190.

[3] Liu J, Wang Y, Qu X, et al. In vivo quantitative bioluminescence tomography using heterogeneous and homogeneous mouse models [J]. Opt Express, 2010, 18(12): 13102-13113.

[4] Cong W, Wang LV, Wang G. Formulation of photon diffusion from spherical bioluminescent sources in an infnite homogeneous medium[J]. Biomed Eng Onlin, 2004, 3(1): 12.

[5] Kim AD. Transport theory for light propagation in biological tissue[J]. JOSA A, 2004, 21(5): 820-827.

[6] Ripoll J, Schulz RB, Ntziachristos V. Free-space propagation of diffuse light: theory and experiments[J]. Phys Review Lett, 2003, 91(10): 103901.

[7] Chen X, Gao X, Qu X, et al. A study of photon propagation in freespace based on hybrid radiosity -radiance theorem[J]. Opt Express, 2009, 17(18): 16266-16280.

[8] Wang G, Li Y, Jiang M. Uniqueness theorems in bioluminescence tomography[J]. Med Phys, 2004, 31(8): 2289-2299.

[9] Cong W, Wang G, Kumar D, et al. Practical reconstruction method for bioluminescence tomography[J]. Opt Express, 2005, 13(18):6756- 6771.

[10] Lv Y, Tian J, Cong W, et al. A multilevel adaptive fnite element algorithm for bioluminescence tomography[J]. Opt Express, 2006, 14(18): 8211-8223.

[11] Jiang M, Zhou T, Cheng J, et al. Image reconstruction for bioluminescence tomography from partial measurement[J]. Opt Express, 2007, 15(18): 11095-11116.

[12] He X, Liang J, Qu X, et al. Truncated total least squares method with a practical truncation parameter choice scheme for bioluminescence tomography inverse problem[J]. J Biomed Imag, 2010: 291874.

[13] Yu J, He X, Geng G, et al. Hybrid multilevel sparse reconstruction for a whole domain bioluminescence tomography using adaptive fnite element[J]. Comput Math Method Med, 2013: 548491.

[14] Lewis EE, Miller WF. Computational methods of neutron transport[M]. Michigan: Wiley, 1984.

[15] Tian J, Liu K, Lu Y, et al. Evaluation of the simplified spherical harmonics approximation in bioluminescence tomography through heterogeneous mouse models[J]. Opt Express, 2010, 18(20): 20988-21002.

[16] He X, Zhang Z, Yu J. Trust Region Method for Solving the Bioluminescence Tomography Inverse Problem [C]. IEEE SOPO, 2010: 1-4.

[17] Liu J, Wang Y, Qu X, et al. In vivo quantitative bioluminescence tomography using heterogeneous and homogeneous mouse models[J]. Opt Express, 2010, 18(12): 13102-13113.

An Optimal Automatic Selection Algorithm of Permissible Source Region Applied in Bioluminescence Tomography

【Writers】Zhang Qian, Chen Chunxiao, Liu Gao, Kan Xingxing, Li Tingting Department of Biomedical Engineering, Nanjing Univesity of Aeronautics and Astronautics, Nanjing, 210016

Objective An optimal automatic selection method of permissible source region is proposed to reduce the ill-conditioned and ill-posed problems in the reconstruction of the light source in bioluminescence tomography. Methods The 2D images captured by CCD are mapped into surface light irradiance distribution based on the light propagating model. The relation matrix between the source and light distribution is obtained by fnite element method. Permissive source region is determined by using the automatic selection method proposed in this paper, and then Tikhonov regularization is applied to reconstruct the light source. Results The center point distance between the optimal permissible source region and true source is 1.26 mm, and the center point error of the reconstructed light source and true source is 0.47 mm, the volume error is 9.13 mm3. Conclusion The optimal permissive source region selection strategy is effective to locate the permissive source region close to the true source, and reduces the reconstructed error due to subjective orientation of permissible source region. This proposed method is the basis of high precision source reconstruction in bioluminescence tomography.

bioluminescence tomography, permissible source region, forward problem, inverse problem

TP391.41

A

10.3969/j.issn.1671-7104.2014.06.001

1671-7104(2014)06-0393-05

2014-05-12

国家自然科学基金面上项目(61171059)；南京航空航天大学研究生创新基地（实验室）开放基金(kfjj201427)；中央高校基本科研业务费专项资金(NP2012202, NZ2014101)

陈春晓，教授，E-mail: ccxbme@nuaa.edu.cn