Origin在“研究金属冷却规律”实验数据处理中的应用

欧颖贤, 张军朋

(华南师范大学 物理与电信工程学院,广东 广州 510006)

0 引 言

金属的冷却规律指金属被加热到指定温度后，在自然对流或强迫对流的情况下，温度随时间变化的规律。虽然研究该规律的实验操作较为简单，但数据处理过程却十分复杂：首先作冷却曲线及各点切线，然后求出切线斜率并求对数，最后运用最小二乘法对所得数据进行线性拟合。如果仅靠传统手工作图及计算将非常耗时，并且带来较大误差。

然而，随着计算机技术的发展，越来越多的软件被运用到大学物理实验[1-5]。其中Origin软件以其形象直观、易学易用、功能开放等特点广泛应用于实验数据处理及分析中[6-7]。例如，利用Origin计算数据平均值和标准偏差[8]、剔除数据异常值[9]、对实验数据进行线性拟合[10]、自定义曲线拟合[11]及多峰拟合[12]等。为了提高实验数据处理的效率和拓展Origin软件使用的范围，本文介绍了利用Origin处理“研究金属冷却规律”实验数据的方法，并展示Origin软件的数据剔除、绘制曲线和分析曲线等功能在提高数据处理精确度和可信度方面的作用。

1 实验原理

质量为M1的金属样品加热后，放在较低温度的介质(如室温的空气)中，样品会逐渐冷却。其单位时间损失的热量为

(1)

式中，C1为金属样品在温度T1时的比热容[13]。根据牛顿冷却定律，样品因对流损失的热量为

(2)

式中：α1为热交换系数；S1为样品表面积；m为常数(强迫对流时，m=1；自然对流时m=5/4)；T1为样品温度；T0为介质温度。由式(1)、(2)可得

(3)

假设在不太高的温度范围内，金属的比热容随温度变化很小[14]，则上式可写成

(4)

式(4)为金属的冷却表达式，对它两边取对数得

(5)

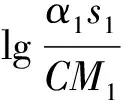
2 实验数据及处理

2.1 实验数据

本实验使用的仪器是DH4603冷却法测量金属的比热容实验装置。选取铜样品加热到120 ℃(热电动势显示约4.93 mV)时，切断电源移去加热源，使铜样品在有机玻璃筒内自然冷却。当温度下降致100 ℃时，每隔30 s记录一次热电动势，连续记录10 min。通过查阅铜—康铜热电偶分度表，利用内插法求出每个热电动势对应的温度值,如表1所示。

表1 铜样品自然冷却的温度变化(室温TO=24.8 ℃)

2.2 数据处理

第一步，数据输入。Origin启动后会自动生成一个工作表Worksheet。首先在表格Data1中输入实验数据，其中冷却时间t的数据置于Time[X]列中，温度T的数据置于Temp[Y]列中(见图1)。

第二步，调用绘图窗口。选中Data1中的Time[X]列和Temp[Y]列，然后点击菜单Plot中的Line+Symbol进行绘图，最后点击左侧工具栏上的按钮T添加图示说明，得到铜样品的T—t冷却曲线(见图1)。

第三步，求曲线上各点斜率。实验要求lg|ΔT/Δt|～lg(T-T0)图，则要先求出ΔT/Δt，即冷却曲线上各个数据点切线的斜率。这可通过Origin曲线分析功能中的“微分”来实现，具体如下：选中Graph窗口，点击菜单Analysis，选择Calculus下的Differentiate。此时，Origin自动对图像进行微分，并弹出新的窗口显示微分图,如图2所示。在项目管理器Project Explorer下，双击“Derivative1”，得到微分数据表，即各数据点的斜率。

第四步，计算引入变量。调出工作表窗口Derivative1，点击菜单Column选择Add New Column新增两列，分别命名为lg1和lg2，用于存放引入变量lg|ΔT/Δt|和lg(T-T0)的值。点击菜单Window选择Script Window调出Lab Talk程序窗口，并输入如下两句命令：

Derivative1_lg=log(abs(Derivative1_Data1Temp));

Derivative1_lg2=log(Data1_Temp-24.8);

得到lg|ΔT/Δt|和lg(T-T0)的值。

第五步，数据的线性拟合。点击菜单Plot中的Scatter，将弹出坐标轴设置窗口。设置lg2为x轴，lg1为y轴后，将出现Graph窗口下的数据点状分布图。因本实验中lg|ΔT/Δt|与lg(T-T0)的关系为线性关

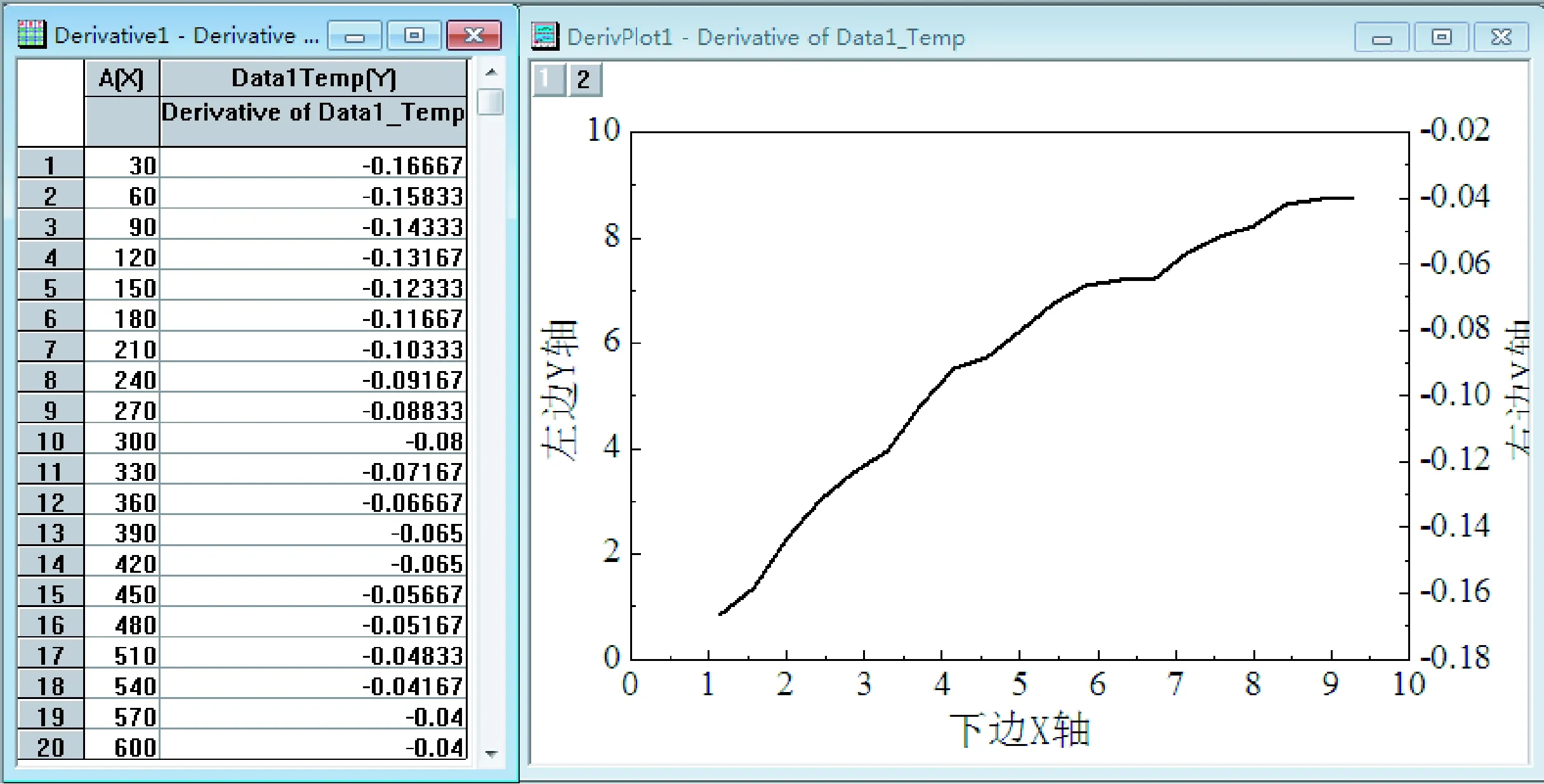
图2 微分数据及微分图

系,故点击菜单Analysis选择线性拟合Fit Linear，Origin将调用最小二乘法线性拟合工具对数据进行拟合。随后，Graph窗口将新增一条拟合直线，同时弹出结果窗口Result Log显示拟合的线性回归方程系数A=-3.000 36，系数B=1.212，标准差SD=0.015 65，相关系数R=0.997 14，如图3所示。

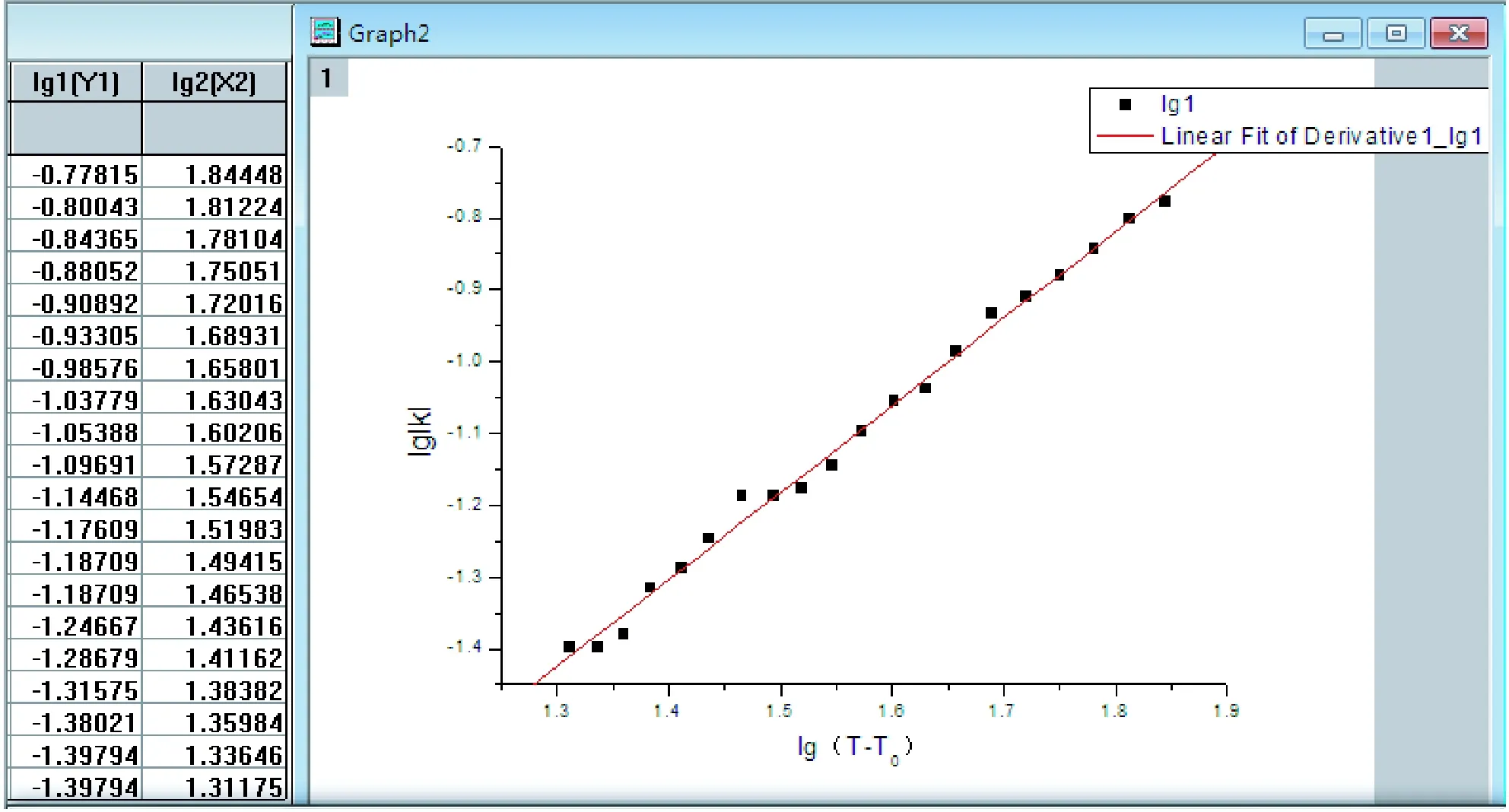
图3 数据线性拟合结果

第六步，异常值的判断。从拟合曲线与数据点的分布情况可看出，其中第14个数据点偏离曲线稍远，因此采取以下步骤对数据进行判断。首先，调出数据窗口Derivative1，点击菜单Column选择Add New Column新增一列，命名为Residual，存放残差。然后，调出Lab Talk程序窗口，输入如下命令：

Derivative1_Residual=-3.00036+Derivative1_lg2*1.212-Derivative1_lg1;

得到Residual列的值，即残差。

本次实验n=20，由肖维勒准则[15]可知ω20=2.24。再新增一列，命名为Contrast，用于存放|Residual|-ω20·σ，并在Lab Talk程序窗口中输入如下命令：

Derivative1_Contrast=abs(Derivative1_Residual)-2.24*0.01565;

在Contrast列中，只有第14个数据为正值，即|Residual14|>ω20·σ，故图像中第14点应该剔除。

第七步，异常值的剔除。在窗口Derivative1中选中第14个数据，右击鼠标，选择Mask下的Apply，屏蔽该行数据(此时该行数据变为红色，见图4)。

图4 异常值剔除后的线性拟合结果

第八步，异常值剔除后的线性拟合。按照前面的方法，对剩下的19个数据点进行拟合，得到剔除异常值后的系数A=-3.014 46,系数B=1.219 72,标准差SD=0.013 1,相关系数R=0.998 09,新的拟合曲线如图5所示。

2.3 实验结果

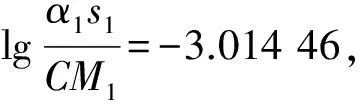
(6)

3 结 语

本文详细介绍了利用Origin软件分析处理“研究金属冷却规律”实验数据的方法及步骤。通过运用Origin软件中的绘图及微分功能，避免了传统方法中利用坐标纸手绘曲线和切线而引入的误差；通过调用软件自带的线性拟合工具，提高了数据拟合的速度；通过编制命令剔除异常数据，获得了更加准确的冷却表达式。由此可见，Origin软件的操作简单快捷，结果直观准确。

此外，利用Origin软件还能快速获取丰富的信息。例如，如果得到其他金属样品的冷却曲线和斜率，即可直接用冷却法求出该金属的比热容，这是传统数据处理方法无法做到的。又如，教师可以根据线性拟合的相关系数R了解学生的实验情况，并指导学生寻找实验误差的来源。

综上所述，将Origin软件引入物理实验有利于提高实验结果的精确度，也有利于提高提高实验的效率。

[1] 吴利华. Matlab在大学物理实验教学中的应用[J].实验科学与技术，2009，7(2)：101-103.

WU Li-hua. Application of Matlab in Physics Experiment[J]. Experiment Science & Technology，2009，7(2)：101-103.

[2] 徐敏莲，邹 静，斯塔洁,等.基于C语言和Origin7.5的曲率法测普朗克常量[J].实验室研究与探索，2012，31(6)：92-95.

XU Min-Lian， Zou Jing， Si Ta-jie. Testing Planck Constant with Curvature Method Based on C language and the Software of Origin7.5[J].Research and Exploration in Laboratory，2012，31(6)：92-95.

[3] 王悦悦，戴朝卿，赵丽华.用Maple软件辅助《大学物理实验》教学[J].实验科学与技术，2009，7(2)：56-57.

WANG Yue-yue，DAI Chao-qing，ZHAO Li-hua. Application of Maple Software in College Physics Experiment Teaching[J]. Experiment Science & Technology，2009，7(2)：56-57.

[4] 卢森杰，马江剑，芦立娟.基于EViews6．0软件下的普朗克常量测定[J].物理通报，2012，10：76-80.

LU Sen-jie，MA Jiang-jian，LU Li-juan. Testing Planck Constant with EViews6．0[J]. Physics Bulletin，2012，10：76-80.

[5] 许定生，白志刚，周炎辉.用微机处理冷却实验数据[J].大学物理实验，1999，12(4)：57-59.

XU Ding-sheng，BAI Zhi-gang，ZHOU Yan-hui. Cooling Experiment Data By Computers[J]. Physical Experiment of College，1999，12(4)：57-59.

[6] 周剑平.Origin实用教程(7.5版)[M].西安：西安交通大学出版社，2007.

[7] 张 杰.用Origin进行物理实验数据处理[J].物理教师，2007，28(5)：50-51.

ZHANG Jie. Data Processing by Using Origin[J].Physics Teacher，2007，28(5)：50-51.

[8] 曹国红.Origin软件在物理实验数据处理中的应用[J].物理教师，2008，29(5)：38-39.

CAO Guo-hong. Physics Experiment Data Processing by Using Origin Software[J]. Physics Teacher，2008，29(5)：38-39.

[9] 王 鑫，吴先球，蒋珍美,等.用Origin剔除线性拟合中实验数据的异常值[J].山西师范大学学报，2003，17(1)：45-49.

WANG Xin，WU Xian-qiu，JIANG Zhen-mei. Data Rejection in Linear Fitting Using Origin[J]. Journal of Shanxi Normal University，2003，17(1)：45-49.

[10] 陈旭红.用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据[J].江苏技术师范学院学报，2006，12(6)：85-89.

CHEN Xu-hong. Experimental Data Processed by Linear Regress and Nonlinear Curve Regress Using Software of Origin[J].Journal of Jiangsu Teachers University of Technology，2006，12(6)：85-89.

[11] 王茂香，李相银.利用Origin软件处理霍尔效应实验数据[J].实验科学与技术，2011，9(5)：43-45.

WANG Mao-xiang，LI Xiang-yin. Data Processing in the Experiment of Hall Effect by Using Origin Software[J]. Experiment Science & Technology，2011，9(5)：43-45.

[12] 张建华，黄树聪，徐常威.中性红电离平衡体系吸收光谱的高斯多峰拟合[J].实验室研究与探索，2012,31(1)：4-8.

ZHANG Jiau-hua，HUANG Shu-cong，XU Chang-wei. Multi-Peaks Gaussian Fitting on UV-visible Electronic Absorption Spectra of Neutral Red Aqueous Solutions[J]. Research and Exploration in Laboratory，2012,31(1)：4-8.

[13] 沈元华，陆申龙.基础物理实验[M].北京：高等教育出版社，2003.

[14] 万纯娣，王永新，万春花,等.普通物理实验[M].南京：南京大学出版社，2000.

[15] Taylor. R. An Introduction to Error Analysis[M].California：University Science Books Press，1982.