倾泻流体研究及数值模拟

于光远, 宋 楠, 杨 雄, 潘永华, 高惠滨

(南京大学 物理学院， 江苏 南京 210093)

0 引 言

在倒水时，我们发现自然倾泻的水流可能会发生分节的情况[1]，出现所谓水“波节”现象。通过实验重复这一现象，并记录大量数据来找出影响这一现象的因素。实验过程中又发现了水流旋转的“水麻花”现象[2]，新现象促使我们设计新仪器和建立新模型，并重复更多的实验，结合相关知识分析讨论，并用计算机模拟，找出现象的本质。

1 实验现象

实验所用出水管管口分别有圆口和方口两种，如图1、2所示。实验中使用水泵供水，流量计调节流量。图1为水“波节”现象，使用圆口装置，可以明显看出下泻水流分成了类似“波节”的形状，即图中H2段。图2为水“麻花”现象，使用非对称方口装置，可以明显看出下泻水流发生旋转[3]。

记录数据是由高清摄像头记录实验影像，再从视频影像中抽样读数得到实验数据。

2 水“波节”模型建立

2.1 流速模型

2.1.1流速模型1

首先考虑的是出水速率均匀分布情况。实验采用半径r=3.50 cm的圆口装置,如图3所示。当水流量Q=100 L/h时，水流经过的管口宽度为L=3.78 cm。因此,水流经过的管口面积S=1.42 cm2,如图3中阴影部分所示。进而可求得此时平均水流速率v=Q/S=0.196 m/s。

图1 水“波节”现象图2 水“麻花”现象

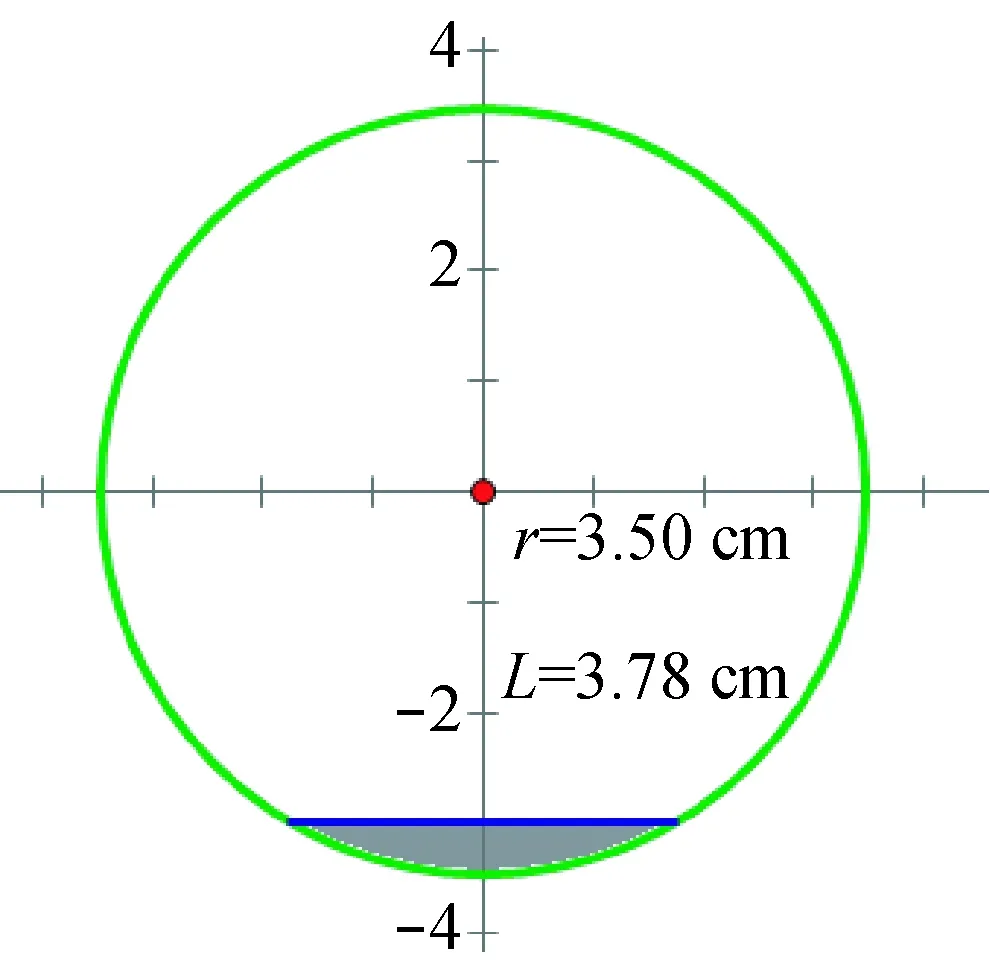
图3 圆口装置示意图

2.1.2流速模型2

流速模型1比较粗糙，求出的速率只能作为参考。一般情况下水流速率不是严格相等的，故建立模型2。

水在圆筒中流动时，各流层为自管道中心开始而半径逐渐加大的圆筒形[4]。中心处流速最大，随着半径的增大而流速逐渐变小[5]。当它的密度ρ及黏滞系数η为常数时，列出相关的流体动力学基本方程[6]。

连续性方程：

divv=0

(1)

运动方程：

(2)

式中,F是单位质量流体所受的力。

式(1)可写成：

(3)

式(2)可写成：

(4)

(5)

(6)

式中，u、v、w是速率在x、y、z轴方向的分量。

在等直径圆截面直管中，流体作平行流动(不考虑起始段)，所有质点都沿同一方向运动，只有一个不为零的速度分量。如取直角坐标系，并把运动方向取作x轴,则

v=0,w=0

(7)

在仅考虑重力而忽略电磁力等的情况下，F=g，为了简便，令

(8)

将式(7)、(8)代入式(5)、(6)，得：

(9)

可见p′仅是x的函数,即p′=p′(x)。将式(7)代入式(3)，得：

(10)

将式(7)～(9)代入(4)～(6)，得：

(11)

由于是稳定流动，∂u/∂t=0,上式变为

(12)

上式左边只与y,z有关，而右边只与x有关，所以它们都必须等于同一常数，即：

常数

(13)

换成柱坐标为

(14)

两次积分得：

(15)

式中，系数简化为k。r0是圆口半径，假设边沿处速率为0，则c=1，得到

(16)

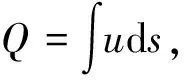
(17)

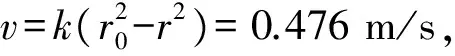
2.1.3流速模型3

模型2的缺陷在于要求边沿流速为零，而边沿处水流较多，为了保证流量，中心速率就过高。因此模型2也应进行修正，必须考虑到边沿处流速不为零，修正后的模型如下式所示：

(18)

则边沿速率为

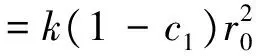
(19)

图4是流量为100 L/h时的实验截图，现以其为例来求解模型3中的系数k、c1和中心速率。因为在管口处，水流喷涌而出以后主要受到来自水的表面张力的作用。表面张力改变了边缘液滴的速度方向，使其向中心靠拢[7]。对于一个直径1 mm的液滴，受到的表面张力约为其重力的45倍。表面张力使得边沿速度方向发生了改变，离开管口以后，速度方向近似指向水流中央。于是可以先利用水流在竖直和水平方向上的位移，求出水流运动时间t和u边，再计算k、c1，最后求得中心速率:0.5gt2=0.028 4,t=0.076 1 s,u边=0.014 3/t=0.188 m/s。

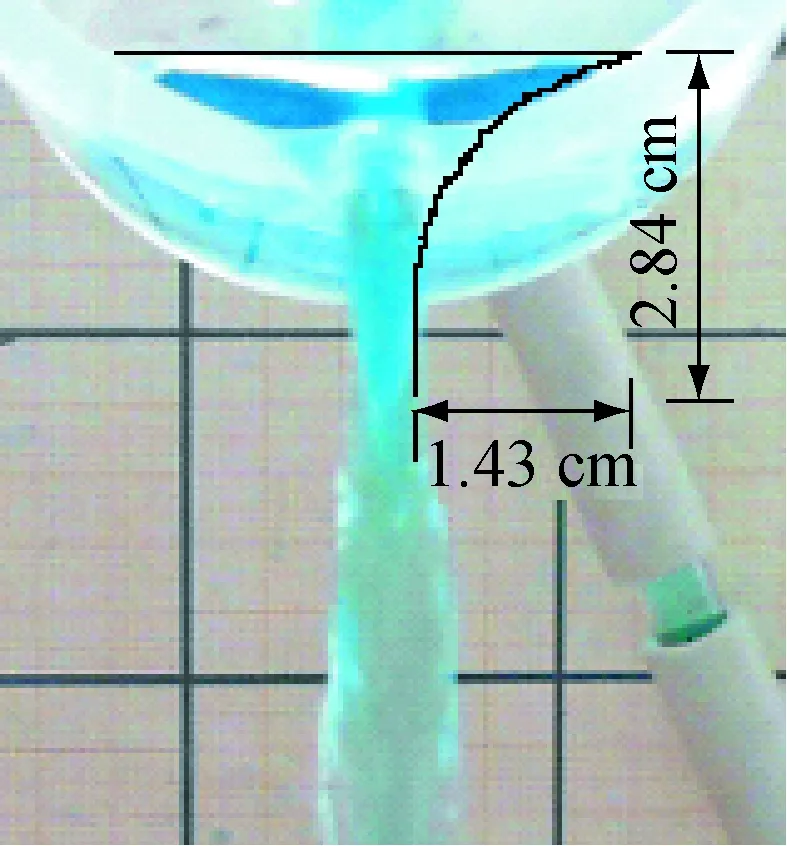
图4 Q=100 L/h实验截图

将Q=100 L/h和u边=0.188 m/s代入式(17)和(19)得:k=225.43,c1=0.319。最后求得中心速率v=0.214 m/s。该结果与实际情况比较相符。

综上所述，模型1为我们提供了平均速率作为参考，以模型2为基础的模型3求解出了圆口模型的速率分布，且中心速率与平均速率非常接近，是比较理想的模型。

2.2 波长模型

2.2.1实验观察

实验中只能明显地观察到2个“波节”点，如图5中A、B所示。考虑到水流在交会碰撞之后水平速率会降低，由于表面张力作用，分散的水流逐渐向中间靠拢。再一次交会时水平速率已经比较小，所以不会再明显地分开，观察不到新的“波腹”和“波节”。

2.2.2猜想假设

把“波节”点间距称之为“波长”，通过实验观察到圆口装置半径相同时，流量越大，“波长”越长。我们觉得影响“波长”的关键物理量是速率，速率正比于流量，反比于圆口半径的平方。所以猜想“波长”H与流量Q之间的函数关系可以表示为

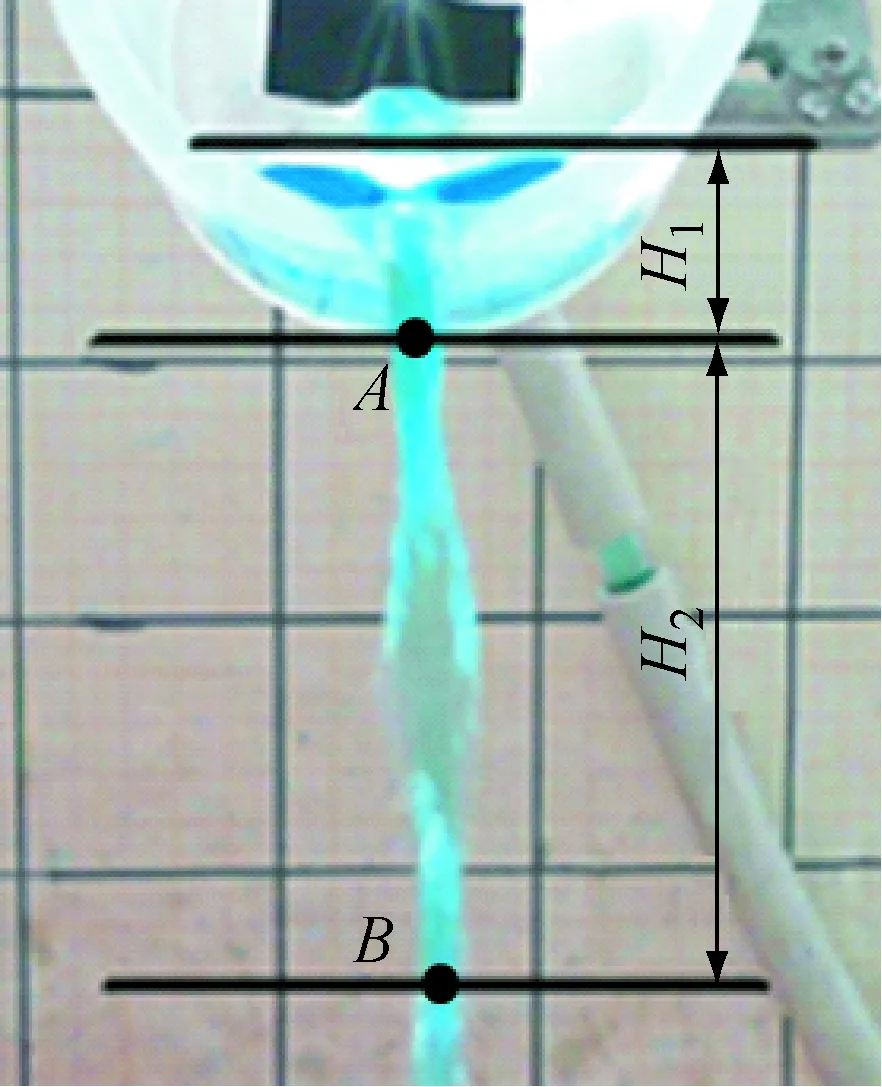
图5 “波长”-流量关系实拍标注图

H=A(r)·Q+c2

(20)

实验中测得的H2是A、B两个“波节”点之间的距离，也就是“波长”被重力拉长之后的长度。可以利用H1与H2计算出“波长”H。

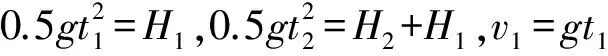
(21)

2.2.3实验验证

实验中，测量了在不同管口直径和不同流量下的“波长”值，结果如表1所示。结果表明,对于同一流量，不同管口直径下的“波长”变化不大，说明系数A(r)近似是一个常数。

根据表1中数据，以流量Q为横坐标，“波长”H为纵坐标绘制“波长”-流量关系图，如图6所示。通过直线拟合得到“波长”-流量关系为

H=1 215.600 3Q+0.001 43

(22)

相关系数R=0.957 94。

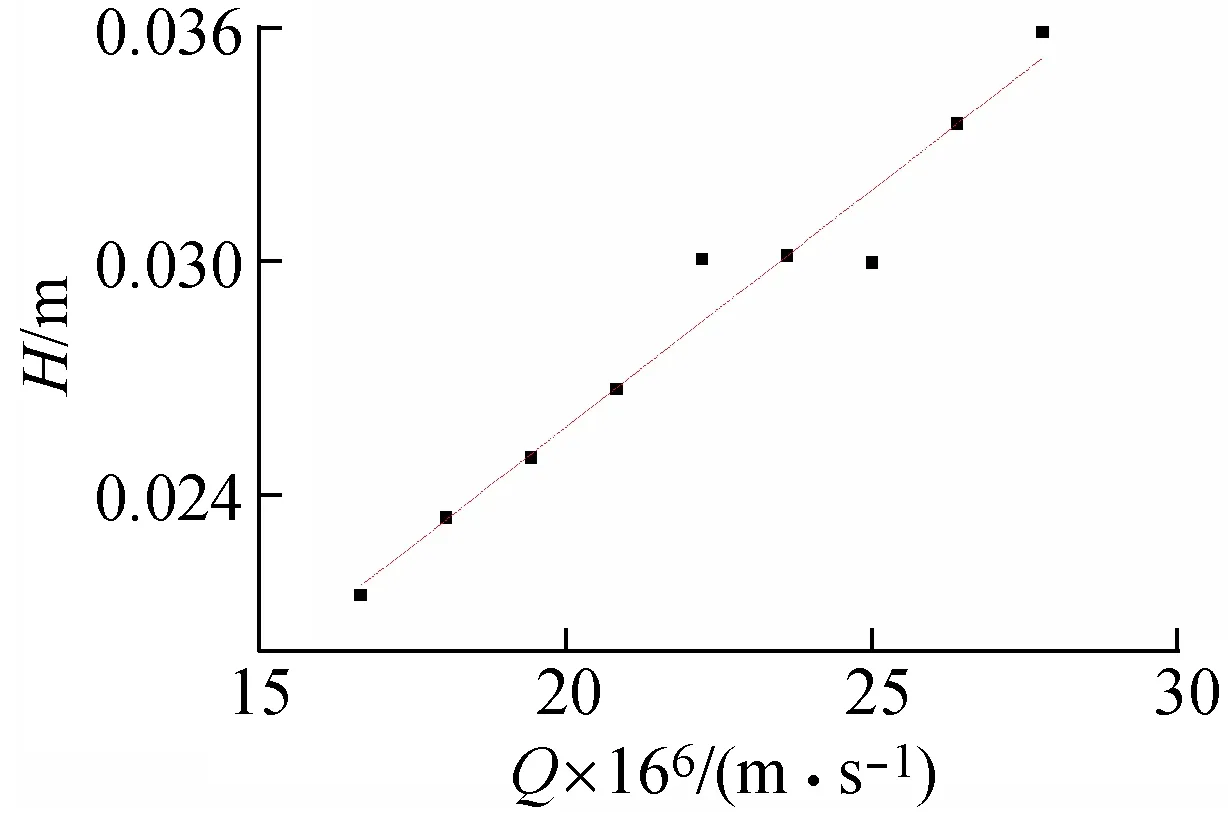
图6 “波长”-流量关系图

我们选取的流量范围与平时生活中能接触到的流量比较接近。可见在该范围内，“波长”与流量近似呈线性关系。

3 水“麻花”模型

水“麻花”现象是在研究水“波节”现象中发现的，考虑到可能是由于出水口处的水流速率分布不均造成了这种现象[8]。由此设计出扁形方口左右不对称型的出水仪器，利用其不对称性人为制造速率分布的不对称[9]。实验结果验证了猜想。

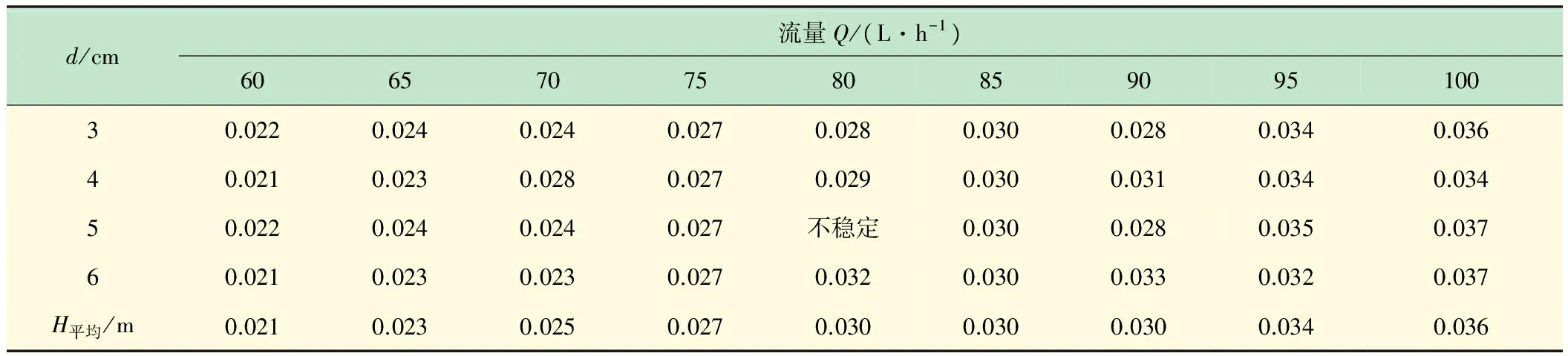
表1 波长H与流量Q关系数据 m

水“麻花”速率分布分析推导。当我们将方形口的高度缩小到较小时，可以视为其高度方向上速率均匀分布，进而可以将很薄的方形口流出的水流视为对一层水流进行近似的模拟[10](见图7)。

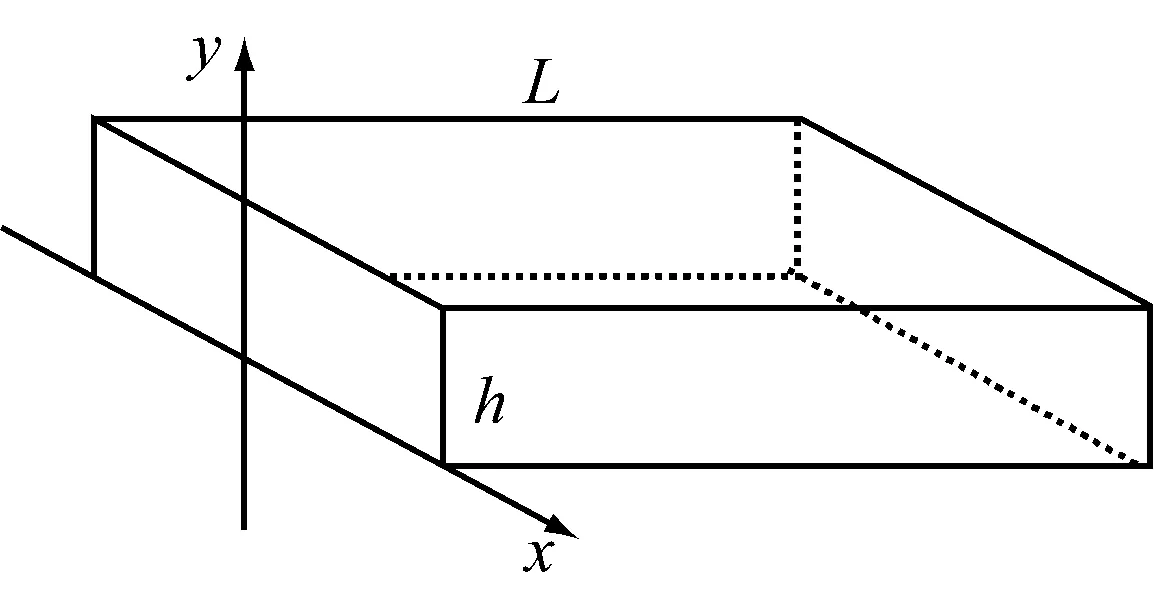
图7 水流薄层模型图

取出与对称轴y距离为x处的液滴微元进行分析[11]，

式中，n为黏滞系数。因为是定常流动，有

F=(Pa-Pb)hdx

式中，Pa、Pb为两端压强，视为恒定，得

所以，vx=ax2+bx+c。

水流与一个振幅衰减的驻波非常相似，考虑到液体之间的黏滞力以及表面张力,根据流体运动形式，猜想x轴方向上的速率函数为[12]

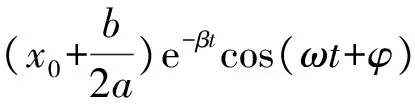
(23)

根据管口处初始速率分布式(18)以及x轴方向上的速率式(23)进行编程模拟。模拟结果可以验证所推公式的实用性。

4 水“波节”现象计算机模拟

4.1 水“波节”现象中出水口水流俯视图模拟[11]

实验中拍摄到的出水口水流俯视图如图8所示。模拟时，先利用实验测量数据求出管口两侧水流的相遇时间t，再根据管口处每个微元的位置求出它的速率v[13]，之后将y=vt作为纵坐标，管口位置作为横坐标，绘制出出水口水流俯视模拟图，如图9所示，可以看出与实际情况符合得比较好。

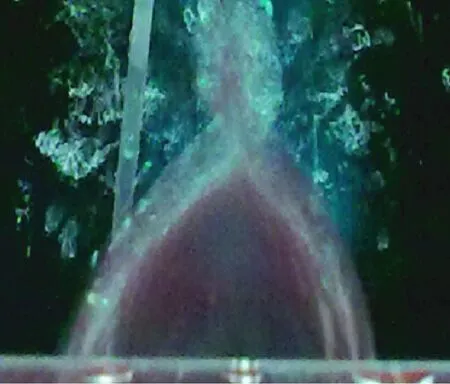
图8 出水口俯视图

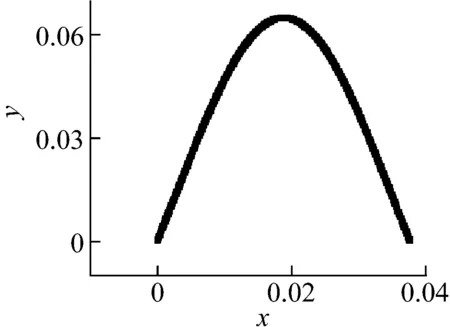
图9 计算机模拟俯视图

4.2 水“波节”现象中出水口水流正视图模拟

图10是实验中拍摄到的出水口水流正视图。利用式(18)、(26)，令b=0，选取适当的β及ω，由计算机生成数据，绘制出出水口水流正视模拟图[14]，如图11所示。可以看出，两者依然符合得比较好，这也就从模拟的角度验证了模型3的正确性。

图10 出水口正视图图11 计算机模拟正视图

4.3 水“麻花”现象计算机模拟

通过以上分析，用软件Origin作出模拟图。

设定管口处的初始速率分布左侧较快，可以得到左侧水流压过右侧水流并向右偏的模拟图像，如图 12所示。并且，从上俯视时可以看出，水流是逆时针的旋向[15]，这与实际情况(见图 13)是相符的。类似地，当设定管口处的初始速率分布右侧较快时，可以得到右侧水流压过左侧水流并向左偏的模拟图像。

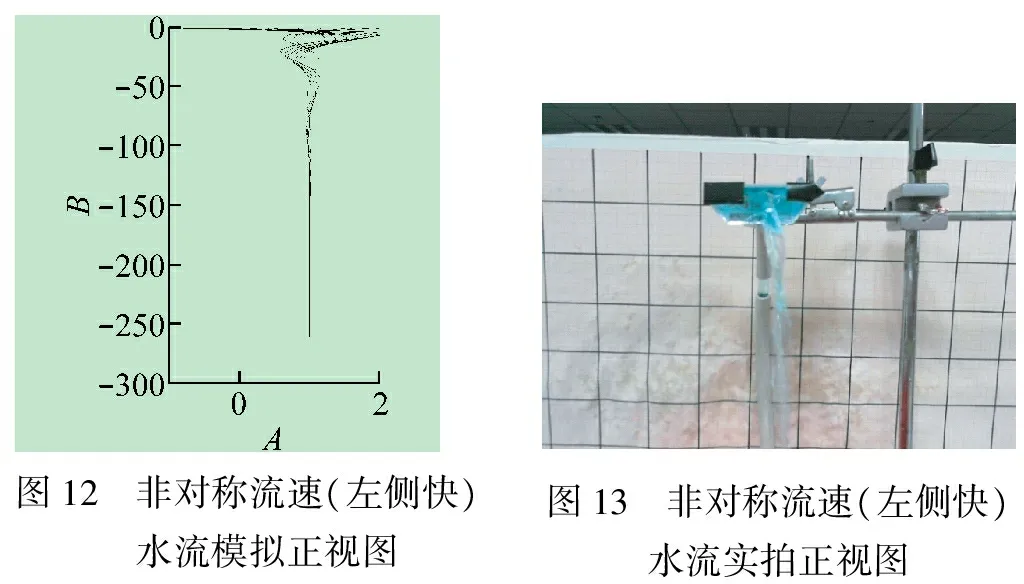
图12 非对称流速(左侧快)水流模拟正视图图13 非对称流速(左侧快)水流实拍正视图

由模拟图像与实际图像的对比可以看出，管口处水流的初始速率分布的不对称确实是造成水流产生旋转的主要原因。

5 结 语

根据以上研究可以得出一些比较确定的结论。

水“波节”现象：当倾泻水流均匀地通过规则的出水口时，在流速不太快、流量不太大情况下，下泻的水柱会出现分节现象，且这种水“波节”的“波长”和流量呈近似的线性关系，与出水口的半径无明显关系。

可以计算出流速分布近似是二次函数分布，在远离轴线的对称位置上，速率近似一致。此时水流不发生明显的旋转，而会产生类似“波节”的现象。

水“麻花”现象：如果水流倾泻时，水流于出水口两侧速率分布不对称，此时下泻水流会发生旋转，形成螺旋下泻的水流，并且速率大的那侧水流将会位于上方。此时仍要求流速不太快，流量不太大。

[1] 容 琼. 一种螺旋流发生器的数值试验研究[D]. 武汉：武汉理工大学，2007.

[2] 刘少东. 轴向漩涡流动的理论分析[D]. 成都：西华大学，2009.

[3] 王晓飞. 管内螺旋流的实验研究与分析[D]. 武汉：武汉理工大学，2004.

[4] 贺成才. 圆管分层层流的流动规律[J]. 西南石油学院学报，2002,24(6)：82-84.

He Cheng-cai. The law of laminar flow in pipe[J]. Journal of Southwest Petroleum Institute, 2002,24(6)：82-84.

[5] 吴 望. 流体力学[M]. 北京：北京大学出版社，1983：145-155.

[6] 谢雨浩. 泊肃叶公式的一般推导[D]. 桂林：桂林医学高等专科学校，1984.

[7] 刘 非. 弯曲水流中固液两相运动夹角的研究[D]. 上海：上海交通大学，2012.

[8] 傅天清. 简单圆孤曲线弯道水流特性研究[D]. 山西：太原理工大学，2003.

[9] 贾兴豪，彭向和，龙血松. 导流板改善弯管流场的数值模拟与优化[J]. 西南大学学报,2011,33(3):139-143.

Jia Xing-hao, Peng Xiang-he, Long Xue-song. The numerical simulation and optimization of bend flow field improved by the deflector[J]. Journal of Southwest University, 2011,33(3):139-143.

[10] 杨忠国，郑 鑫，解恒燕. 计算流体力学湍流模型在喷管流场数值模拟中的比较[J]. 黑龙江八一农垦大学学报，2010,22(5)：36-38.

Yang Zhang-guo, Zheng xin, Xie Heng-yan. The comparison of turbulence models of Computational fluid dynamics in the nozzle flow field numerical simulation[J]. Journal of Heilongjiang Bayi Agricultural University, 2010,22(5)：36-38.

[11] 朱林海. 基于物理模型的水流动画计算机模拟[D]. 西安：西北工业大学，2002.

[12] 史力生. 用数字直接模拟层流[J]. 长沙铁道学院学报，1994,12(2)：43-54.

Shi Li-sheng. Directly digital simulation of laminar flow[J]. Journal of Changsha Railway University，1994,12(2)：43-54.

[13] 翟 明，董 芃，王希影. 圆管层流脉动流动的数值模拟[J]. 哈尔滨工业大学学报，2009,41(11):73-76.

Zhai Ming, Dong Peng, Wang Xi-ying. The numerical simulation of pulsating flow of laminar flow in pipe[J], Journal of Harbin Institute of Technology, 2009,41(11):73-76.

[14] 喻 宇. 有压管道水流冲击气团的局部三维流场数值模拟研究[D]. 哈尔滨：哈尔滨工业大学，2011.

[15] 魏喜飞. 基于物理模型的三维水流模拟研究[D]. 石家庄：河北工程大学，2012.

好奇——创新意识的萌芽;
兴趣——创新思维的营养;
质疑——创新行为的举措;
探索——创新学习的方法。