安庆铜矿充填体内破坏区和非破坏区地震波衰减规律研究

袁本胜，史晓鹏，郭利杰，董凯程

（1.北京矿冶研究总院，北京 100160；2.金属矿山智能开采技术北京市重点实验室，北京 100160）

安庆铜矿充填体内破坏区和非破坏区地震波衰减规律研究

袁本胜1，2，史晓鹏1，郭利杰1，董凯程1

（1.北京矿冶研究总院，北京 100160；2.金属矿山智能开采技术北京市重点实验室，北京 100160）

本文首先采用爆破震动测试法对充填体内的地震波进行测试，然后根据数理统计原理运用最小二乘法进行方程回归拟合，获得测试区段充填体内破坏区和非破坏区的地震波衰减公式，进而通过解方程求算充填体内安全允许震速。然后采用声波测试法根据声波传播速度的变化分析爆破引起的充填体破坏状况验证所求得的充填体地震波衰减公式和安全允许震速的正确性。

地震波；衰减规律；充填体；爆破

随着胶结充填等充填新工艺的逐渐完善，采用充填采矿法的矿山比例逐年增加，本文所述矿山即采用了充填采矿法开采。随着采矿作业的不断开展，该矿形成了两面充填体中矿柱回采、三面充填体下矿房回采以及充填体下水平矿柱回采的局面。为了在回采过程中有效保护充填体，首先需要了解充填体的震动破坏特性。本文首先采用爆破震动测试法回归拟合充填体破坏区和非破坏区的地震波衰减公式，然后通过解方程求得充填体内安全允许震速；然后采用声波测试法根据声波传播速度变化分析爆破引起的充填体破坏状况以验证所得充填体内破坏区和非破坏区的地震波衰减规律的正确性。

1 充填体概述

被测矿区地层主要为三迭系中上统灰岩和粉矽岩，出露于矿区的东部与南侧，露头发育程度中等，地层较为完整。矿岩主要成分为大理岩、矽卡岩和闪长岩。矿体倾向西南，倾角较陡。矿区构造基本为单斜层，地层走向为北西－南东，倾向东北，倾角中等至平缓。矿区褶皱主要有西马鞍山背斜和龟形山背斜。断层和褶皱带较发育，对矿床影响明显，构造发育程度中等。

测试场地位于－400m水平7＃采场充填体中间部位，在－400m至－460m天井联络道中－416m位置延伸原来的充填体调查横巷，横巷深20m，宽1.5m，测点和爆源点均布置在横巷顶板。

对1＃矿体7＃、9＃矿房－488m、－471m 和－416m水平充填体做了开挖调查，并对取得的150个试样进行了测试，其平均强度为0.78MPa，其中在本次试验点位置所取试样的平均强度为0.72MPa。

矿山生产过程中，1∶10配比的充填料浆平均浓度为70.38%，28天和60天强度平均值分别为1.14MPa、1.44MPa；1∶10配比浓度为70%～73%的充填体试块28天抗压强度试验室试验结果为1.23M～1.34MPa。

2 测试系统搭建

爆破震动测试系统由传感器、震动测试仪和微型计算机等组成。传感器为磁电式垂直型震动速度传感器，它为弹簧－质量系统，当物体震动时，由于惯性导致线圈与磁钢相对运动，切割磁力线人而在线圈内产生感应电压。震动测试仪采用高速微控制器，将速度传感器输出的电压量进行处理，然后由12位高速A/D转换器对电压量进行量化并将量化结果保存到存储器内。通过该仪器与计算机的RS－232串行接口通信可将测试的数据结果存入计算机磁盘，之后利用配套软件即可进行分析处理。

声波速度测试采用数字存储示波器和计算机采集和存储波形。根据双通道波形起始点判读直接得出两测点间声波传播时间，由此和两点间距离即可求出传播速度。当充填体破坏时，波速会有不同程度的降低；反过来，根据同一测试区间的波速变化可分析充填体的破坏状况。

测点包括震动速度测点和声波速度测点，均布置在巷道顶板，见图1。震动速度测点共8个，编号为1＃～8＃。声波速度测点有2个，编号为a和b。图中A、B、C、D、E为5个爆破用钻孔，垂直向上，孔深0.5 m。

图1 测试点位置示意图

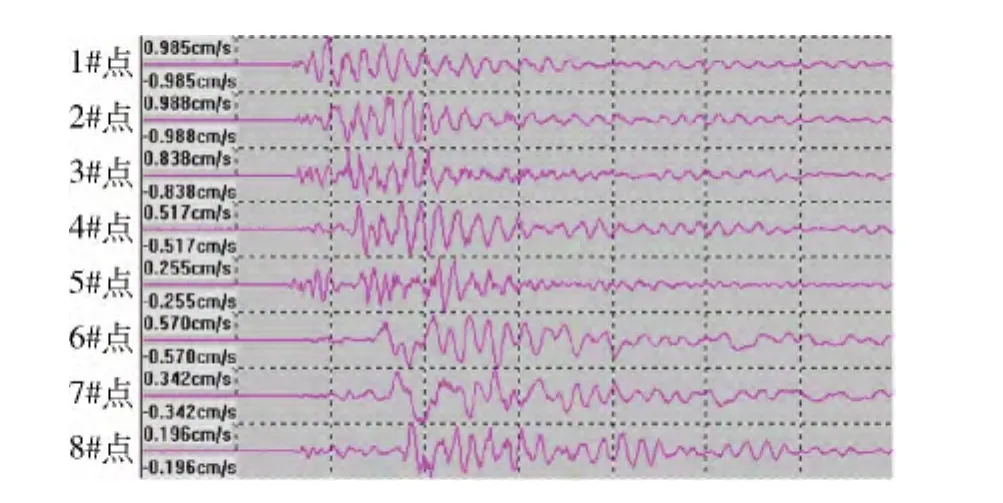
图2 第1次测试获得的波形图

3 爆破震动衰减规律分析

图2为第1次测试获得的波形（限于篇幅，其他波形略）。根据5次测试获得的波形，经过计算得出比例药量和峰值震速结果见表1。

比例药量：ρ＝Q1/3/R，式中 Q 表示炸药量，齐发爆破时为总装药量，微差爆破时为最大一段装药量，单位kg；R表示测点与爆破中心的距离，m。

峰值震速：V＝震动测试仪测得的峰值电压/传感器灵敏度。

从表1可以看出，在5次测试中，比例药量取值范围为0.0232～0.2656kg1/3/m，峰值质点震动速度最小值为0.88cm/s，最大值为14.85cm/s。峰值质点震动速度与比例药量在双对数坐标系中的散点图参见图3。从散点图可以看出，当比例药量由小逐渐增大时，震速的变化趋势也是由小变大，但当比例药量较大时，震速增长趋势变慢，大约在0.1时出现拐点。此拐点可以理解为充填体破坏区和非破坏区的分界点，它的值即是本文需推算的临界比例药量及与之对应的临界震速，而关键之所在就是如何确定此拐点。

表1 5次爆破震动测试的比例药量和峰值震速

具体推算方法为：按比例药量由小到大的顺序逐渐增加回归点并进行回归，同时作相关系数和F检验。当检验值出现拐点时，即以此前检验的最佳值对应的回归公式作为正常状态下（也即非破坏状态下）充填体的地震波衰减公式。再按比例药量由大到小的顺序逐渐增加回归点并进行回归，同时作相关系数和F检验以得出非正常状态下（也即破坏状态下）充填体的衰减公式。两条回归线的交点即是所求的临界比例药量和临界震速。

3.1 非破坏状态下充填体中地震波衰减规律

从比例药量小于0.07的所有点开始回归，然后按比例药量由小到大的顺序逐点加入进行回归（因篇幅所限，回归分析数据表略）。

回归曲线相关系数R范围为0.722～0.907，若在0.05水平检验，查相关系数检验表得出其范围为0.304～0.381，实际回归得到的R均超出该范围，表明地震波在充填体内的衰减规律按公式V＝K（Q1/3/R）α拟合的效果较好。对 F 值在 0.05 和0.01水平检验，查F分布表可得其范围分别为4.08～4.24和7.31～7.77，而上表中的 F 值在25.048～147.725之间，全部超出查表值，可见拟合的曲线关系高度显著。比较各次回归的剩余标准差s，以s值最小为优，也就是说以s为最小值时回归得出的K、α值作为未被破坏的充填体中地震波衰减公式的K、α值。从表1中数据可求出，未被破坏的充填体中地震波衰减公式见式（1）。

3.2 破坏状态下充填体中地震波衰减规律

对于充填体破坏区的地震波衰减公式回归，数据选取按比例药量从大到小的顺序取至其稍小于0.1（未被破坏的充填体中地震波衰减公式回归取点的最大比例药量为0.1027）即可。

根据前述非破坏区充填体同样的计算方法得到破坏区充填体中地震波衰减公式（式（2））。

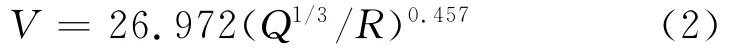
最终获得的破坏区和非破坏区充填体中地震波衰减公式的回归线见图3。

将破坏区和非破坏区充填体中地震波衰减公式（1）、式（2）联立解方程得到安全允许震速 V＝9.22cm/s，对应的比例药量ρ＝0.0955kg1/3/m。

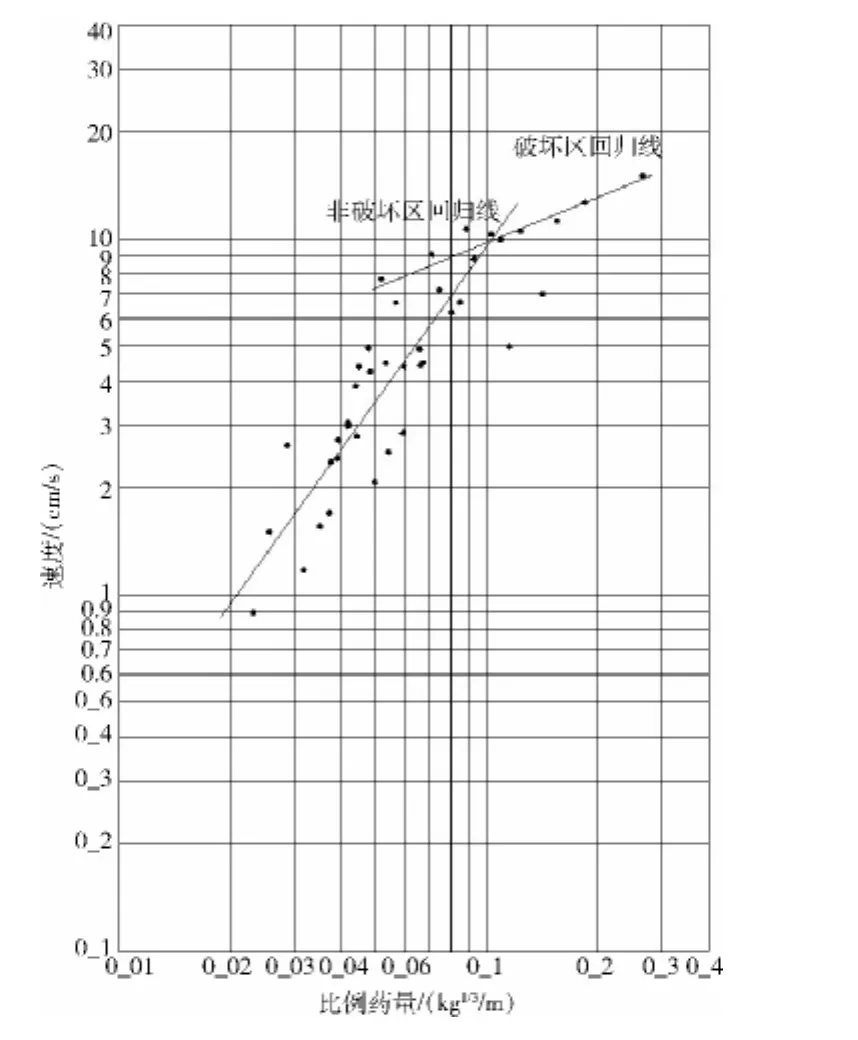
图3 破坏区与非破坏区充填体中震动数据散点与回归线

4 利用声波测试法验证衰减规律

声波速度测试点为2个固定接收点，通过锤击人为产生声源。锤击点与接收点同在一条直线上。两接收点的距离为0.71m。在5次测试爆破之前和前4次爆破之后都进行了声波测试，双通道数据采集器记录的波形分别见图4。取得的声波传播时间和经计算得出相应的声波传播速度见表2。

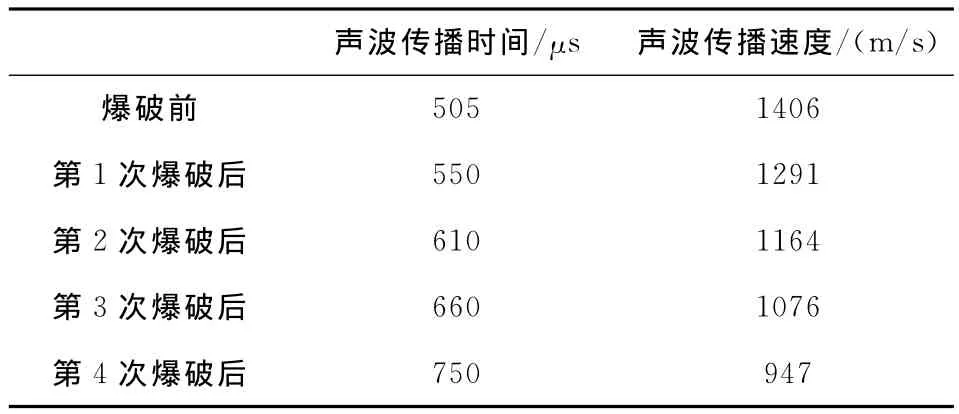
表2 充填体声波测试数据

由表2可知，从第1次爆破后波速就开始减小，以后各次比前一次也都减小。由此可见，第1次爆破就已经对两测试点的充填体产生破坏，且随着爆源的逐渐靠近，破坏程度越来越严重。

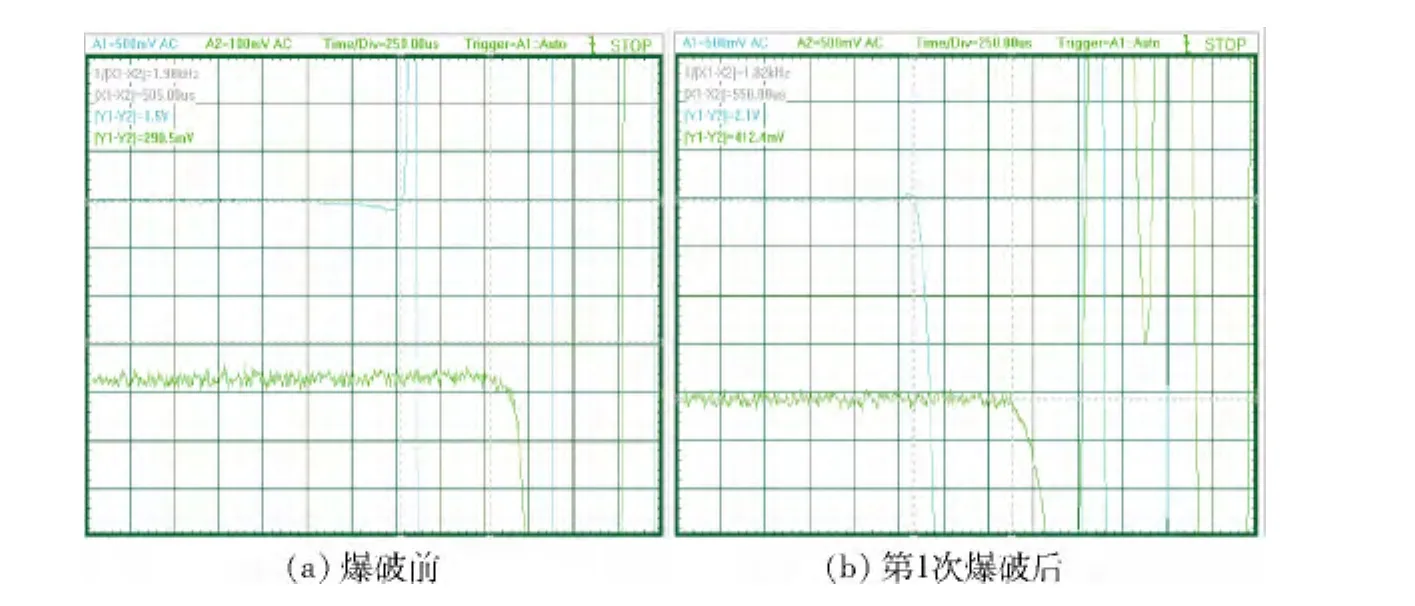
图4 声波测试波形

按式（1）计算，在第1次爆破时，药量为0.075kg，爆心与第a和b两测试点的距离分别为3.8 6 m和4.6 m，求得此二点的峰值震速分别为11.27cm/s和8.67cm/s。两测试点所求得的峰值震速在前文所求得的安全允许震速9.22cm/s的两边，说明充填体被破坏的位置在两测试点之间。

上述由爆破震动和声波速度测试分析两种方法所得结论一致，相互验证了正确性，充分说明本研究对具体充填体条件进行实测得出的衰减公式和安全允许震速是可信的。

5 结论

本文对同一次爆破采用爆破震动测试数值拟合法和声波测试法两种方法对爆破震动在充填体内的衰减规律进行测试，并根据数理统计原理运用最小二乘法进行方程回归拟合，取得测试区段充填体内破坏区和非破坏区的地震波衰减规律，并辅以声波速度测试反映充填体破坏状况，验证了前述结果的正确性。获得了如下结论。

1）按比例药量逐点加入回归以剩余标准差s判优，并利用相关系数的显著性检验和F检验在未知破坏区和非破坏区的情况下找出了此二区两条回归线的回归系数，据此划定两区界线，从而确定充填体内安全允许震动速度。

2）对于本测试的充填体，灰砂比为1∶10时，充填体非破坏区的震动衰减公式为V＝307.912（Q1/3/R）1.494。

3）对于本测试的充填体，灰砂比为1∶10时，充填体破坏区的震动衰减公式为 V＝26.972（Q1/3/R）0.457。其衰减指数明显低于非破坏区的衰减指数，即爆破震动在破坏区的衰减慢。场地系数也因充填体被破坏而明显减小。

4）对于本测试的充填体，灰砂比为1∶10时，安全允许震动速度为9.22cm/s。

5）可通过测量充填体内两个点的声波速速来判断充填体的破坏状况。

［1］赵刚，张银平.DSVM系列测振仪在爆破振动测试中的应用［J］.工程爆破，1995，1（4）：61－65.

［2］胡建华，雷涛，周科平，等.充填采矿环墇境下爆破振动效应预测与控制［J］.2009，26（4）：81－84.

［3］吕涛，石永强，黄诚，等.非线性回归法求解爆破振动速度衰减公式参数［J］.岩土力学，2007，28（9）：1871－1878.

［4］李洪涛，舒大强.爆破震动衰减规律的影响因素［J］.武汉大学学报：工学版，2005，38（1）：79－82.

［5］LI Hong－tao，SHU Da－qiang.Influential factors analysis of blasting vibration attenuation law［J］.Engineering Journal of Wuhan University，2005，38（1）：79－82.

［6］ZANGXiu－ping，WANG Hong.Preliminary exploration of the velocity attenuation equation form of blast vibration ［J］.Metal Mine，2002（4）：36－37.

［7］臧秀平，刘升宽，董涛.露天爆破振动参数衰减模型研究［J］.有色金属：矿山部分，2005，57（5）：31－33.

［8］张继春，彭琼芳.岩体爆破地震波衰减规律的现场试验与分析［J］.辽宁工程技术大学学报：自然科学版，2001，20（4）：399－401.

［9］叶洲元，周志华.爆破震动安全距离的优化计算［J］.中国安全科学学报，2005，15（3）：57－60.

Study on blasting vibration attenuation law for the failure zone and non－failure zone of backfilling in Anqing copper mine

YUAN Ben－sheng1，2，SHI Xiao－peng1，GUO Li－jie1，DONG Kai－cheng1
（1.Beijing General Research Institute of Mining and Metallurgy，Beijing 100160，China；2.Beijing Key Laboratory of Nonferrous Intelligent Mining Technology，Beijing 100160，China）

At first this paper use the method of the blasting vibration to test the seismic wave on the filling body，then apply the principle of mathematical statistics and the least squares to fit of regression equation，and obtain the attenuation formula of the seismic wave at the failure zone and non－failure zone of the filling body，also by solving the equation to calculate the allowable safety vibration velocity of filling body.At last it use the sound wave test method with its features of that the change of the seisimic wave velocity can indicate the destroys state of the filling body，to validate the attenuation formula of the seismic wave at the failure zone and non－failure zone of the filling body.

seismic wave；attenuation law；backfilling；blasting

袁本胜（1982－），男，汉族，工程师，硕士，主要从事矿山安全监测方向的工作。E－mail：yuanbsh＠163.com。

P631

A

1004－4051（2014）S2－0309－04

2014－10－17

“十二五”国家科技支撑计划项目资助（编号：2013BAB－02B02；2012BAB01B04）；国际合作项目资助 （编号：2011DFA－71990）；北京矿冶研究总院院基金课题资助（编号：YJ－2012－01）；矿山主被动结合高精度微震监测技术与装备研发项目资助（编号：2012BAK09B03）