等高线综合方法的比较与分析

胡 菡，陈春华,2，孙 霞

（1.湖北省测绘工程院，湖北 武汉 430074；

2.精密工程与工业测量国家测绘地理信息局重点实验室，湖北 武汉 430079）

等高线综合方法的比较与分析

胡 菡1，陈春华1,2，孙 霞1

（1.湖北省测绘工程院，湖北 武汉 430074；

2.精密工程与工业测量国家测绘地理信息局重点实验室，湖北 武汉 430079）

从制图综合的约束条件着手，针对等高线的自动综合方法进行研究。提出了等高线综合算法的比较方法，制定出一套等高线综合方法的评价指标并进行了实验，从几何约束、拓扑约束、结构约束等方面验证了这套方法和指标的合理性和可行性。

等高线自动综合；约束条件；道格拉斯算法；算法比较

本文对几种有代表性的等高线综合方法进行比较，寻找各自特点，讨论并得出等高线综合方法评价的方法和标准。

1 等高线综合算法的比较方法

制图综合中的约束源于综合控制中的要素。本文力图通过对制图综合约束条件的分析来建立评价指标，以判断等高线综合算法的可靠性和适用性。一般情况下，约束条件可以分为几何约束、拓扑约束、结构约束和格式塔（Gestalt）约束等几类。

1.1 几何类指标

1）等高线点位精度

等高线的位置精度对地形图而言相当重要，其衡量标准定义为抽样点在综合前的位置到该点所在原始等高线综合后得到的等高线的最短距离。

2）等高线长度比

一般而言，综合后的等高线长度会小于综合前。对于同一根等高线而言，其长度在综合后越小，说明综合程度越大。因此，在某些参数相同的情况下，可以通过等高线综合前后的长度比，从侧面反映算法的综合程度。同时，也可以通过等高线长度比的变化，衡量等高线综合算法的合理性及算法的稳定性。

1.2 拓扑类指标

1）拓扑信息量

等高线之间存在的严格的序关系，被视为等高线的拓扑关系，可以用等高线树来表示。可以把闭合的等高线看成面，对于不可能相交的等高线而言，其构成的面与面之间的拓扑关系主要有包含、相离两种。将这种拓扑关系表现成树结构，则可将包含关系定义为父子关系，而相离关系定义为并列关系。

在此基础上，就可以对等高线的拓扑信息量进行量算。假设等高线树中等高线Ci有Ni个邻居结点，根据邻居结点个数对结点进行分类：有1个则属于分类1，有2个则属于分类2，…。设Ci的邻居共属于Mi种分类，第j类邻居共有nj个，则第j类邻居出现的概率为：

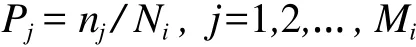
等高线Ci的拓扑信息量为：

2）拓扑错误数量

等高线自动综合中的拓扑错误主要包括等高线的自相交、自重叠以及与相邻等高线之间的相交、重叠等。

1.3 结构类指标

1）地形结构

综合前后制图区域的地形结构能否得到保持，是衡量等高线综合算法的一项重要指标。本文通过分析提取出的汇水线的相似程度，来判断等高线综合算法在地貌形态结构保持方面的优劣。

2）等高线高程分布

通过对等高线的高程信息，如高程极大值、极小值、算术平均值、标准差等的比较、分析，可以判断出不同等高线综合算法对高程数据的保留是否合理。

格式塔及其他指标包括等高线光滑程度、数据压缩程度、算法化简时间等，这里不一一说明了。

2 实验分析

选择我国南方某地作为实验样区。根据等高线的形态和地形的平坦程度，选取了两块数据区域，大小均为1 500 m×1 500 m，平均高程分别为289.581 m和214.763 m，等高距5 m。

实验选用Douglas-Peucker算法和三维Douglas-Peucker算法进行比较，它们分别属于二维、三维以及直接、间接等高线综合方法，具有较强的代表性。实验在保留相同的特征点数下进行，以保证其他指标比较时的公平性。

两块实验样区的原始数据以及二维道格拉斯、三维道格拉斯算法综合后的数据如图1所示。

图1 样区综合前后等高线图

2.1 点位精度

分别从两块数据中选取30个样点，通过量算、统计，得到这60个抽样点的偏移量。根据比较，综合前后点位的偏移量，二维道格拉斯算法较三维道格拉斯算法普遍小。另一方面，三维道格拉斯算法综合前后点位偏移量的标准差较二维道格拉斯算法偏大，说明三维道格拉斯算法在点位精度保持上的稳定性较差。

2.2 等高线长度比

对二维道格拉斯算法而言，所有的长度比均小于1，即综合后等高线长度较综合前要小，这符合一般规律。对三维道格拉斯综合算法而言，绝大部分长度比小于1，但抽样数据中也有一根等高线综合前后长度比略大于1。从等高线长度比的方差得出，二维道格拉斯综合算法得到的等高线长度比较稳定；三维道格拉斯综合算法得到的等高线长度比不仅存在大于1的可能，而且其在平均值附近摆动的幅度远大于二维道格拉斯算法。

2.3 拓扑信息量

分析综合前以及用两种算法综合后的两块实验数据的等高线图，得到如图2所示的两组等高线树。

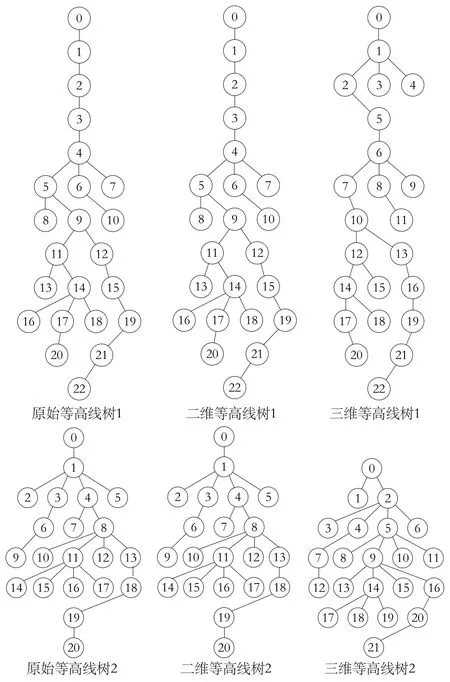
图2 样区综合前后等高线树

在等高线树基础上对等高线的拓扑信息量进行了量算，如表1和表2。

表1 拓扑信息量偏差统计

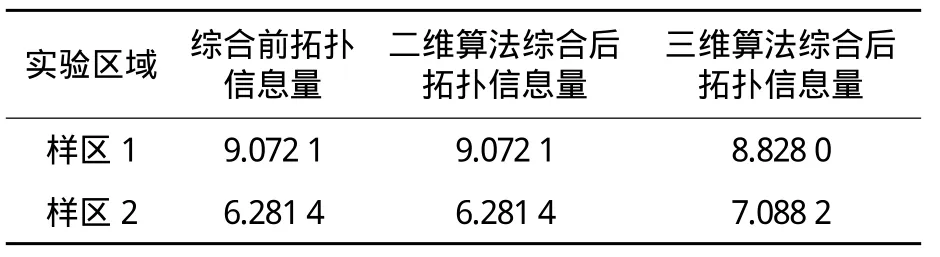
表2 总体拓扑信息量统计

由表可知，对于二维道格拉斯综合算法，无论是单根等高线拓扑信息量，还是等高线图的总体拓扑信息量，均没有变化。而三维道格拉斯算法的拓扑信息量有较大的改变，这主要是因为三维道格拉斯算法针对整个制图区域的地貌形态进行综合，而后内插生成新的等高线，内插过程中难免会造成等高线拓扑关系的变化。

2.4 拓扑错误数量

三维道格拉斯综合算法在本次实验中没有出现等高线相交、重叠或其他拓扑错误。而二维道格拉斯综合算法在两块实验数据的综合结果中出现等高线自相交、自重叠各1次。

2.5 地形结构

分别将综合前后实验数据转换为格网数据，生成矢量的河网数据，并对其进行统计和量算，得到河网分级情况及各级河流长度，如表3。

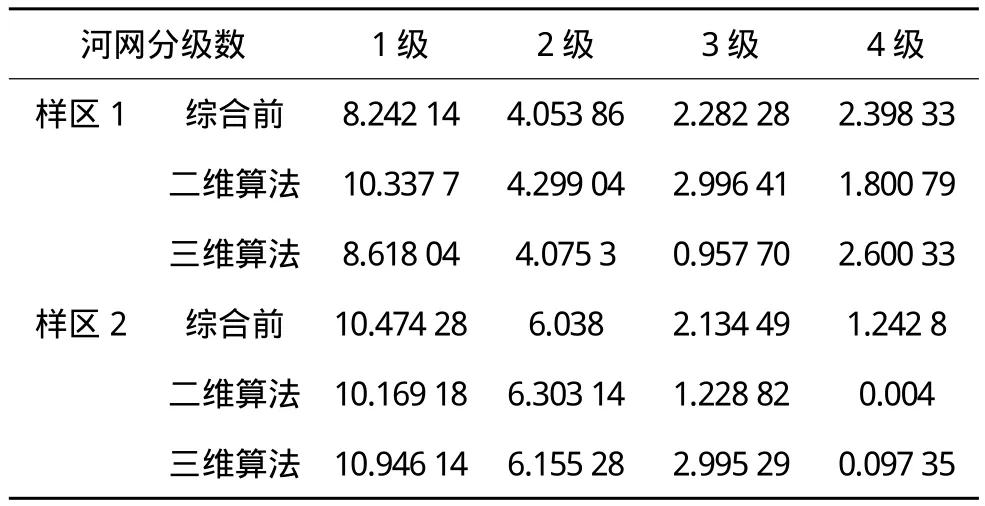
表3 河网分级统计/km

下面对河网分级数据进行分析和比较。以综合前的河网分级数据为标准，计算二维和三维道格拉斯算法综合后的河网分级情况与综合前河网分级情况的偏差，来比较两种综合算法对地形结构的保留情况，如表4所示。

表4 河网分级偏差统计/km

从表4可以明显看出，三维道格拉斯算法对地形结构的保持较二维道格拉斯算法好，两块实验数据的河网分级偏差均较二维算法小。三维道格拉斯算法在地形结构保持方面明显优于二维算法，这也非常符合三维道格拉斯算法从整体地貌综合出发的特点。

2.6 高程分布

通过实验比较得到的高程信息分布情况如表5。

可以明显看到，用三维道格拉斯综合算法综合得到的等高线特征点数据与综合前的原始数据的高程信息分布相当接近；而二维道格拉斯算法综合得到的等高线数据与原始数据的高程信息分布差别则较大。这说明在高程信息的保留方面，三维道格拉斯综合算法有明显的优势。

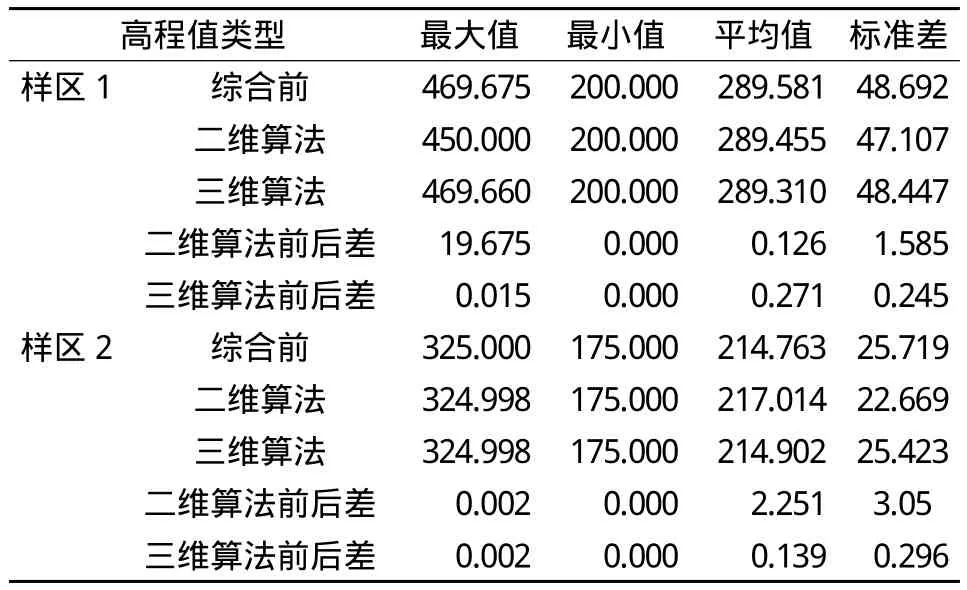
表5 高程信息统计/m

2.7 数据压缩程度、等高线光滑程度

采用单根等高线在综合前后的点数比衡量等高线光滑程度。三维道格拉斯算法在保留了地形特征点后内插生成的等高线，较二维算法从原始等高线上保留特征点直接生成的等高线光滑。但这也从一个侧面反映出，要保持等高线光滑，其数据量必定较大。但三维道格拉斯算法在保留了地形特征点后，可利用不同的内插方法控制等高线上点的疏密，以达到控制数据量、等高线光滑程度等目的，灵活性大。

2.8 算法耗时

通过实验比较得出，二维道格拉斯算法综合等高线所花的时间明显长于三维算法，可以认为三维道格拉斯算法综合效率更高。

3 结 语

本文从制图综合的约束条件着手，建立了一套等高线自动综合方法的比较指标。从实验结果来看，这套指标可以反映不同等高线综合方法的特点及其在各方面的优劣。实验结果符合算法的特性，反映了这套比较指标的合理性和可行性。但在等高线综合方法的比较研究方面，仍有大量工作有待探讨，如建立合理的数学模型以更全面、更精确地对各项指标进行度量；探索对各项指标进行综合评价的模型与方法；寻求量化格式塔约束的合理方法；通过比较有针对性地改进综合算法。

[1] Fei Lifan, Huang Lina, He Jin. An Indirect Generalization of Contour Lines Based on DEM Generalization Using the 3D Douglas-Peucker Algorithm[C]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing, 2008

[2] 郭庆胜,毋河海,李沛川.等高线的空间关系规则和渐进式图形简化方法[J].武汉测绘科技大学学报,2000,25(1)：31-34

[3] 艾廷华,祝国瑞,张根寿.基于Delaunay三角网模型的等高线地形特征提取及谷地树结构化组织[J].遥感学报，2003，3(4)：292-298

[4] 查正军.基于数字高程模型（DEM)）的地形特征提取[D].上海：同济大学，2007

[5] 李丽,郝振纯.基于DEM的流域特征提取综述[J].地球科学进展，2003，18(2)：251-256

[6] 朱鲲鹏,武芳.基于约束条件的线要素化简算法质量评估[J].测绘科学，2007，32(3)：28-30

[7] 刘文锴,乔朝飞.等高线图信息定量度量研究[J].武汉大学学报：信息科学版，2008，33(2)：157-159

Comparisons and Analysis of Contour Lines’ Generalization Method

byHU Han

Based on constrain condition of cartographic generalization,this paper set out to study the generalization methods of contour lines. And then, the paper raised the comparison method of contour lines’ generalization algorithm, and formulated a series of evaluation indicators of it, verifying the rationality and feasibility of the method and indicators in geometric constraints aspect, topological constraints aspect, structure constraints aspect by experiments.

generalization of contour lines, constraint condition,Douglas-peucker algorithm, algorithm comparison

P283.1

B

1672-4623（2014）02-0141-03

10.11709/j.issn.1672-4623.2014.02.051

2013-05-31。

项目来源：精密工程与工业测量国家测绘地理信息局重点实验室开放基金资助项目（PF2011-30）。

胡菡，研究方向为地图数据处理及其理论研究，数字城市和地理信息系统应用与开发。