武汉城市公园系统空间结构分形研究

刘大均，胡 静，王 娟

(1.华中师范大学城市与环境科学学院，武汉430079;2.中国旅游研究院武汉分院，武汉430079)

0 引言

城市公园是城市居民旅游休闲空间的重要组成部分，其空间分布形态对于城市生态环境建设以及提高居民生活质量具有重要意义［1］。随着经济社会的快速发展及城市化进程的加快，城市居民对旅游休闲的关注度和参与度不断提升［2］。城市公园作为国民旅游休闲设施建设的重要内容，已成为衡量城市国际竞争力的重要标志［3］，日益受到学术界的重视，逐渐成为地理学研究的重要内容。国外学者主要从城市公园的区域影响［4-5］、环境感知［6-7］、空间服务范围［3］、空间分布的公平性［8］、空间规划以及选址［9-10］等方面开展研究。国内相关研究主要集中在城市公园的规划设计［11］、可达性［12］、景观格局［13］、游客行为［14］等方面。但国内外学者对城市公园空间结构的复杂性以及发育程度的相关研究少有涉及，城市公园空间分布规律有待进一步总结。

分形理论产生于20世纪70年代中期，是分析复杂性、非线性、自组织演化系统的理想工具，能精确刻画复杂系统［15］。近年来分形理论常被运用于旅游休闲设施系统空间结构研究［15-17］，然而不同类型和属性的旅游休闲设施系统空间结构具有差异性［15-16］，城市公园是居民闲暇时间最常接触的主要场所［14］，而城市公园系统空间结构分形研究鲜有涉足。本研究以武汉城市公园为例，运用分形理论与方法深入分析武汉城市公园系统空间结构，有助于认识与把握城市公园系统空间分布规律，为国民旅游休闲设施空间格局优化及建设提供依据。

1 研究区域与数据来源

以武汉市主城区为研究空间范围，包括江岸区、江汉区、硚口区、汉阳区、武昌区、青山区、洪山区，总面积888.42 km2。以《武汉市建设年鉴2011》、武汉市园林局公布的城市公园名录及其相关数据为基础，利用Google Earth获取武汉市主城区城市公园的空间位置，并运用ArcGIS 10建立武汉城市公园空间属性数据库，绘制武汉城市公园系统空间分布及核密度图(图1)。

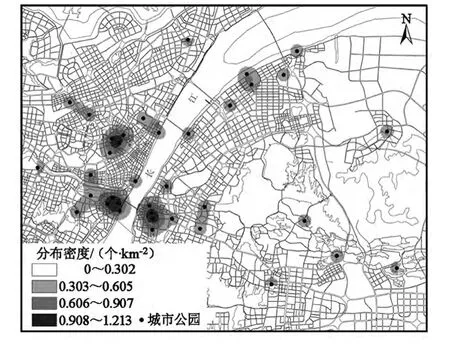
图1 武汉城市公园系统空间分布及核密度Fig.1 Spatial distribution and kernel density of Wuhan city parks system

2 研究方法

2.1 集聚维模型

假定城市公园系统按照自相似规律围绕中心城市公园成凝聚态分布，且城市公园系统分形体是均匀变化的，则可借助几何测度关系确定半径为r的圆周内城市公园数量N(r)与半径r之间的关系，即有:

式中:Df为分维。考虑到半径r的大小会影响分维的数值，可将其转化为平均半径［18］，平均半径为:

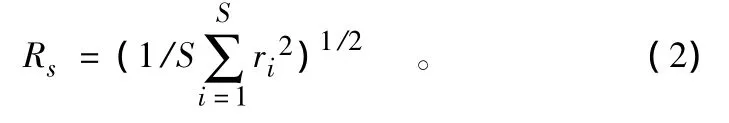
则一般有分维关系:

式中:Rs为城市公园平均半径;ri为i城市公园到中心城市公园的距离;S为城市公园数;D为聚集维，反映了城市公园系统围绕中心城市公园随机聚集的特征［19］。一般而言，0≤D≤2，聚集维D越大，城市公园系统空间分布由中心城市公园向周边衰减越慢，紧致性越弱;反之，城市公园系统空间分布由中心城市公园向周边衰减越快，紧致性越强;当聚集维D=2时，城市公园系统在空间上呈均匀分布的态势。

2.2 网格维模型

在对城市公园系统空间分布进行网格化时，城市公园所占据的网格数N(r)会随着所取的网格尺寸r而变化，若城市公园系统具有无标度性，则应有:

类比豪斯多夫(Hausdorff)维数公式可知，α=D0为分维(称容量维)［19］。观察行号为i、列号为j的网格，设在之中的城市公园分布数为Nij，城市公园总数为N，可定义其概率为Pij=Nij/N，于是有信息量:

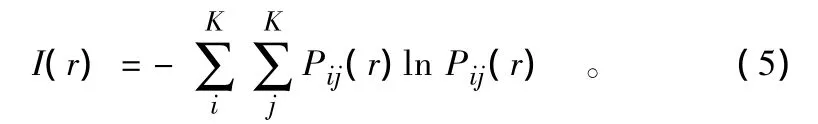
式中:K=1/r为区域分段数。如果城市公园系统是分形的，则应有:

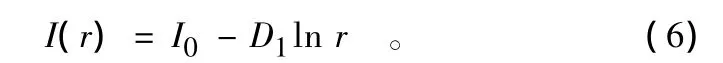
式中:I0为常数;D1为分维(称信息维)［19］，反映城市公园系统在空间上的分布状况。一般而言，0≤D≤2，网格维D越大，城市公园系统空间分布越均衡;反之，则表明城市公园系统空间分布越集中;当网格维D趋近于1时，表明城市公园系统具有集中到某一地理线上的趋势;当D1=D0时，则表明城市公园系统属于简单的分形［19］。

2.3 关联维模型

由于城市公园系统空间研究通常是在二维空间上，因此空间关联函数可定义为［15］:

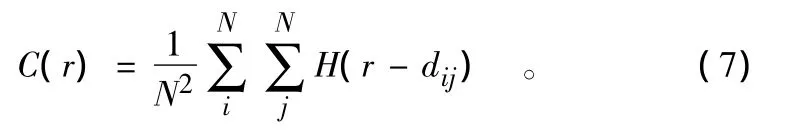
式中:r为码尺(yardstick);dij为i城市公园与j城市公园之间的乌鸦距离(crow distance)［20］;H(r-dij)为 Heaviside函数，即:

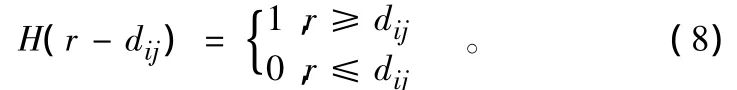
如果城市公园系统空间分布是分形的，则应具有标度不变性，即:

式中:α=D即是分维，可称之为空间关联维数(基于乌鸦距离的关联维数，即乌鸦维)，反映城市公园系统的交通网络的关联性以及通达性［19］。一般而言，0≤D≤2，当关联维D值越大，城市公园系统空间分布越均匀;反之，城市公园系统空间分布越集中。若将乌鸦距离改为乳牛距离［20］，可得到城市公园系统空间结构的乳牛维，便可求出牛鸦维数比ρ。当ρ越接近于1时，表明城市公园系统交通网络通达性越好;反之，表明城市公园系统交通网络通达性越差［19］。

3 结果分析

3.1 集聚维分析

集聚维测算中心通常选取区域首位要素或几何中心要素［16，19］。黄鹤楼公园是武汉的标志性建筑，也是国家5A级景区，因此以黄鹤楼公园作为测算中心，反映武汉城市公园系统空间集聚态势。利用ArcGIS 10空间分析工具测算武汉各城市公园至黄鹤楼公园的欧氏距离ri，并转换成平均距离Rs(表1)，将(Rs，S)绘成双对数坐标图(图2)，用最小二乘法求出武汉城市公园系统的聚集维数值D。

如图2所示，武汉城市公园系统的无标度区宽大(0.693 1 ～3.496 5)，线性拟合状况良好(测定系数为0.989 7)，表明武汉城市公园系统空间结构发育较为成熟。武汉城市公园系统的聚集分维值D=0.990 4＜1，说明武汉城市公园系统围绕中心城市公园呈相对集聚的分布态势，空间分布由中心向四周呈衰减趋势，圈层衰减特征明显。聚集分维值D相对较小，反映出武汉城市公园系统的自组织优化趋势较强，但空间吸附半径不大，系统在演化过程中可能存在多中心并存的局面。结合武汉城市公园系统空间分布和核密度图可进一步发现，武汉城市公园系统在空间上存在3个较为明显的集聚区:即以中山公园、喷泉公园、宝岛公园、小南湖公园等构成的汉口集聚区;以龟山公园、月湖公园、汉阳公园、莲花湖公园、武汉动物园等构成的汉阳集聚区;以黄鹤楼公园、武昌公园、首义文化公园、紫阳公园等构成的武昌集聚区。近年来，由于青山区受城市发展政策以及基础设施建设等因素的影响，武汉新的城市公园集聚区正逐渐形成。

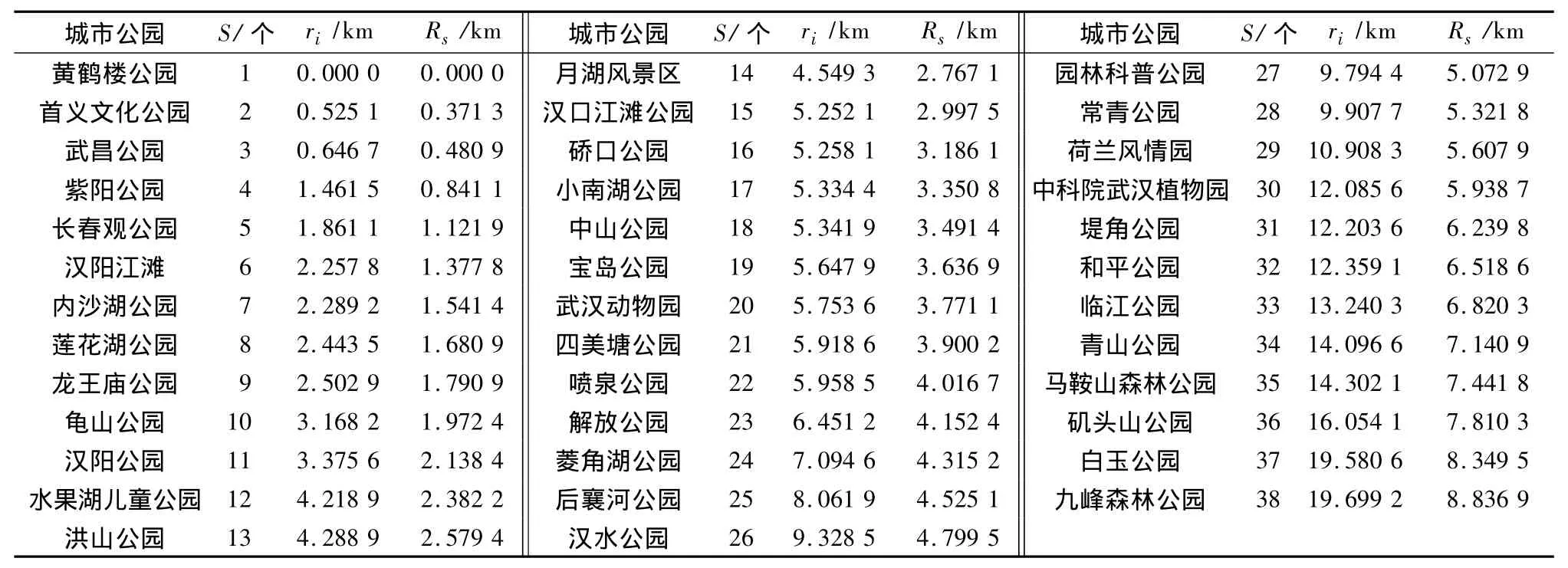
表1 武汉城市公园系统集聚数维测算数据Tab.1 The determining data of aggregation dimension of Wuhan city parks system

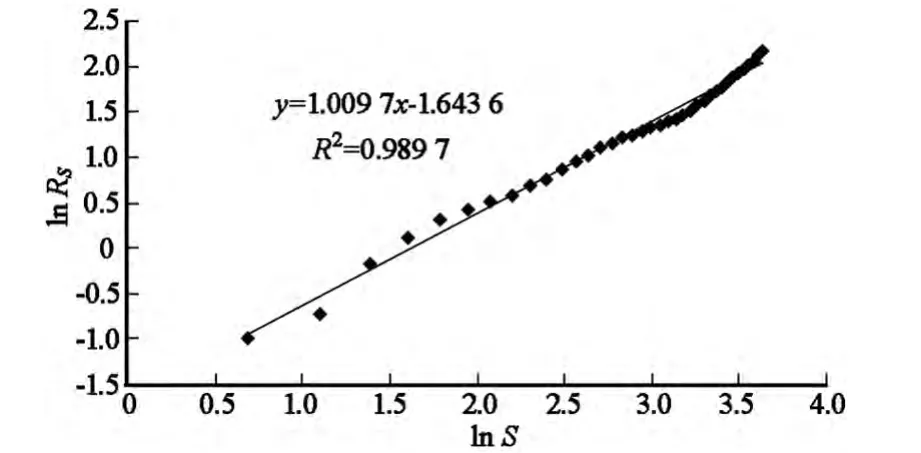
图2 武汉城市公园系统集聚维数双对数散点图Fig.2 The ln-ln plot for the aggregation dimension of Wuhan city parks system

3.2 网格维分析

在武汉城市公园系统空间分布矢量化图上取一矩形，区内含有主城区38个城市公园，可视矩形区域边长为1个单位，分别将各边分成K等分，则研究的区域被分成K2个小区域。统计城市公园所占据的网格数N(r)，统计每个网格内的城市公园个数Nij(r)，算出概率Pij(r)。随着r取值的变化，可以得到相应的N(r)和Pij(r)，并通过公式(5)计算便可得到相应的I(r)(表2)。将(N(r)，K)和(I(r)，K)绘成双对数坐标图(图3)，通过最小二乘法求出武汉城市公园系统的容量维和信息维数值。

表2 武汉城市公园系统网格维数测算数据Tab.2 The determining data of grid dimension of Wuhan city parks system

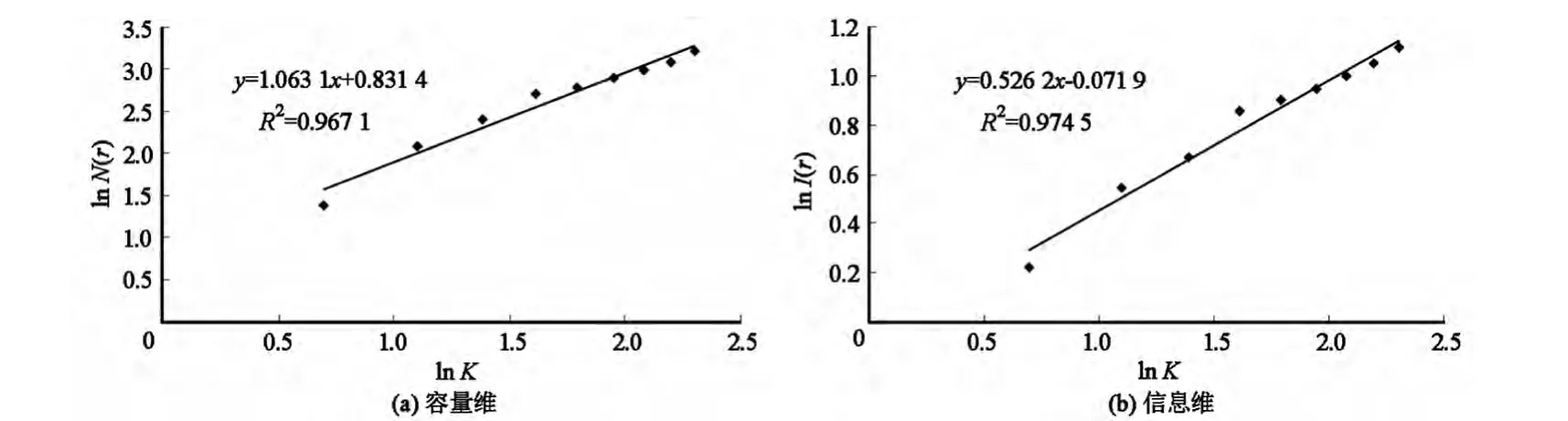
图3 武汉城市公园系统网格维数双对数散点图Fig.3 The ln-ln plot for the grid dimension of Wuhan city parks system

由图3可知，武汉城市公园系统在一定测算尺度上具有明显的无标度区(1.098 6～2.302 6)，城市公园系统空间结构分形特征明显。容量维数值D为1.063 1(测定系数为0.967 1)，接近于1，说明武汉城市公园系统在自组织演化过程中具有向某一地理线集中的趋势。信息维数值D为0.526 2(测定系数为0.974 5)，信息维小于容量维，且相差较大，表明武汉城市公园系统在空间上呈不等概率分布态势，空间分布不均匀性强，分形结构较为复杂。结合武汉城市公园系统空间分布及核密度图可进一步看出，武汉城市公园系统具有向长江、龟山、蛇山等资源禀赋较好的地区集聚以及沿武珞路、汉阳大道、琴台大道、新华路、建设大道等交通轴线分布的特征，受资源禀赋以及交通因素的影响较大。

3.3 关联维分析

利用ArcGIS 10空间分析工具和Google Earth分别测算武汉主城区38个城市公园之间的乌鸦距离和乳牛距离，构建38×38乌鸦矩阵和乳牛矩阵。取步长Δr=2 km，随着所取码尺r的变化，取得一系列N(r)，按关联维模型计算便可得到相应的C(r)(表3，表4)。将(r，C(r))绘成双对数坐标图(图4)。通过最小二乘法求出武汉城市公园系统的乌鸦关联维数值D和乳牛关联维数值D。

从图4看出，武汉城市公园系统在一定码尺分割区间上存在明显的无标度区(1.386 3～3.178 1)，进一步反映出武汉城市公园系统是分形的。乌鸦维数值为0.916 8 ＜1，测定系数为0.937 9，线性拟合良好，表明武汉城市公园系统空间结构较为紧致，自组织演化能力强。武汉城市公园系统乳牛维数值为1.036 5，测定系数为0.963 2。牛鸦维数比ρ接近于1，表明武汉城市公园系统的交通网络通达性好，城市公园之间关联度高。

4 结论与讨论

运用分形理论的集聚维模型、网格维模型、关联维模型对武汉城市公园系统空间结构分析，表明武汉城市公园系统空间结构具有分形特性。武汉城市公园系统在空间上呈相对集聚的分布态势，圈层衰减特性明显。武汉城市公园系统存在汉口、汉阳、武昌3个较为明显的集聚区。武汉城市公园系统分形结构较为复杂，具有向长江、龟山、蛇山等资源禀赋较好的地区集聚和沿武珞路、汉阳大道、琴台大道、新华路、建设大道等交通轴线分布的特征。武汉城市公园系统空间自组织演化能力强，交通网络通达性好，城市公园之间的空间联系紧密。

表3 基于乌鸦距离的武汉城市公园系统关联维数测算数据Tab.3 The determining data of correlation dimension of Wuhan city parks system based on crow distance

表4 基于乳牛距离的武汉城市公园系统关联维数测算数据Tab.4 The determining data of correlation dimension of Wuhan city parks system based on cow distance

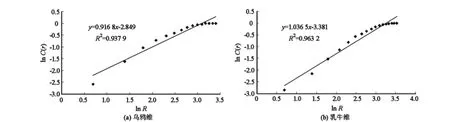
图4 武汉城市公园系统关联维数双对数散点图Fig.4 The ln-ln plot for the correlation dimension of Wuhan city parks system

将分形理论运用于城市公园系统空间结构研究，有助于精确刻画城市公园系统空间结构，揭示城市公园空间分布规律，对城市公园建设以及国民旅游休闲设施的完善具有参考价值。

［1］ 毛小岗，宋金平，杨鸿雁，等.2000—2010年北京城市公园空间格局变化［J］.地理科学进展，2012，31(10):1295-1306.

［2］ 徐秀玉，陈忠暖.基于休闲需求的城市公园服务等级结构及空间布局特征——以广州市中心城区为例［J］.热带地理，2012，32(3):293-299，320.

［3］ Oh K，Jeong S.Assessing the Spatial Distribution of Urban Parks Using GIS［J］.Landscape and Urban Planning，2007，82(1/2):25-32.

［4］ Chiesura A.The Role of Urban Parks for the Sustainable City［J］.Landscape and Urban Planning，2004，68(1):129-138.

［5］ Peters K，Elands B，Buijs A.Social Interactions in Urban Parks:Stimulating Social Cohesion?［J］.Urban Forestry＆ Urban Greening，2010，9(2):93-100.

［6］ Sugimoto K.Quantitative Measurement of Visitors’Reactions to the Settings in Urban Parks:Spatial and Temporal Analysis of Photographs［J］.Landscape and Urban Planning，2013，110:59-63.

［7］ Iojǎ C I，Rozylowicz L，Pǎtroescu M，et al.Dog Walkers’vs Other Park Visitors’Perceptions:The Importance of Planning Sustainable Urban Parks in Bucharest，Romania［J］.Landscape and Urban Planning，2011，103(1):74-82.

［8］ Chang H S，Liao C H.Exploring an Integrated Method for Measuring the Relative Spatial Equity in Public Facilities in the Context of Urban Parks［J］.Cities，2011，28(5):361-371.

［9］ Brown G，Weber D.Public Participation GIS:A New Method for National Park Planning［J］.Landscape and Urban Planning，2011，102(1):1-15.

［10］ Zucca A，Sharifi A M，Fabbri A G.Application of Spatial Multi-criteria Analysis to Site Selection for a Local Park:A Case Study in the Bergamo Province，Italy［J］.Journal of Environmental Management，2008，88(4):752-769.

［11］ 赵天，王月杰，全丽娜.自然和历史交融的城市公园绿地规划探索——以吉林市玄天岭公园规划为例［J］.规划师，2008，24(12):99-102.

［12］ 李小马，刘常富.基于网络分析的沈阳城市公园可达性和服务［J］.生态学报，2009，29(3):1554-1562.

［13］ 马琳，陆玉麒.南京市主城区公园绿地景观格局分析［J］.地域研究与开发，2010，29(3):73-76.

［14］ 李建伟，熊鹏，张競予，等.基于女性主义的城市公园游憩行为时空分异特征研究——以西安市丰庆公园为例［J］.人文地理，2011，26(5):60-64.

［15］ 黄泰，保继刚，刘艳艳，等.城市游憩场点系统结构分形及优化——以苏州市区为例［J］.地理研究，2010，29(1):79-92.

［16］ 黄泰，保继刚，戴学军.苏州城市游憩场点系统空间结构分形［J］.地理科学进展，2009，28(5):735-743.

［17］ 黄泰.国民休闲设施系统结构分异的信息维透视——以苏州为例［J］.旅游学刊，2011，26(9):59-65.

［18］ 陈涛.城镇体系随机聚集的分形研究［J］.科技通报，1995，11(2):98-101.

［19］ 刘继生，陈彦光.城镇体系空间结构的分形维数及其测算方法［J］.地理研究，1999，18(2):171-178.

［20］ Kaye B H.A Random Walk through Fractal Dimensions［M］.Berlin:Wiley-VCH，1989.