从计算机的运算过程刍议四则运算的化归

张 铭，张 红

(1. 扬州职业大学，江苏 扬州 225009;2. 扬州市翠岗中学，江苏 扬州 225009)

文献［1］阐述了“除法是减法的简便运算”，更准确地说，除法的意义是相同数连减的简便运算。文献首先根据形式逻辑的类比推理，初步得出上述结论，然后从四个方面给予解释和说明:一是数形结合的说明;二是古典算经的例证;三是古代汉语的训释;四是计算机运算器的运算机制的佐证。但文献对计算机运算器的运算机制(四则运算部分)，未展开论述。另外除法运算化归为减法运算，及其数学方法论意义，也未及深入讨论。本文根据计算机的运算机制，将除法运算最终化归为加法运算。

1 计算机除法的减法运算过程

关于定点数的原码和补码除法，在计算机的运算器中有两种运算方法:恢复余数法和不恢复余数法。它们的运算机理是相同的:将n 位除法转换成若干次“加减——移位——再加减——再移位……”循环，然后通过硬件或软件来实现。由于计算机的数值数据都是采用二进制的形式，因此其除法运算的加减特性表现得更加淋漓尽致。当商上0 时，表示被除数不够减;当商上1时，表示被除数够减。除的过程，就是连续做加减，然后移位(左移位)的过程。

1.1 恢复余数法

人工做除法时，有一个试商(或者估商)的判断过程，实际上就是判断被除数(或是中间过程中的余数)是不是够减。在计算机的除法运算中，机器是默认试商是1 的。如果减下来的结果是正，表示被除数是够减的，也就是说，试商1 是正确的。如果减下来的结果是负，表示被除数是不够减的，试商1 是错误的，需要改成正确的商0。不仅仅是商需要改正，这时被除数(或中间的余数)已经经过运算而变化了，它也是需要改正的，否则是不能继续往下运算的，为此，必须“恢复”其原来的状态，于是出现了“恢复余数法”的情况。

计算机中恢复余数的过程是:利用减法运算出现的符号位的负脉冲，触发商值取反，即由1 变成0(这是一个逻辑运算)。同时，在余数上再加上原来的除数，从而恢复到正确的余数状态［2］。

1.2 不恢复余数法

不恢复余数法是在恢复余数法的基础上产生的另一种算法。在前面的除法运算中，当商上1而被除数不够减时，只需将商从1 改为0，而不急于恢复“正确”的余数。它只需在下一步运算时，作适当地调整，即通过“有问题的余数”左移位，然后加上除数，就可以继续往下运算了。这是一种“艺高人胆大”的算法。由于除法的减法过程中，穿插了加的过程，所以这种不恢复余数法又称为加减交替法。注意，虽然这一算法在计算过程中不需要恢复余数，但在计算的最后一步，有时还是要恢复余数的。详见下文的例1 和例4。现在的计算机中一般都采用加减交替法［3，4］。

不管是恢复余数法算法，还是不恢复余数法算法，计算机的除法运算过程，实际上就是一连串的减法过程。这种算法的根本依据就是因为除法的实质是减法。

在化归方法中［5］，人们常用的方法有分割法、变形法、映射法等。文献［1］将除法的实质归结为减法时，主要遵循了映射法;将除法运算最终化归为加法运算时，计算机中采用了变形法。

2 四则运算的一次化归:除法化归为减法

除法化归的映射结构见图1。

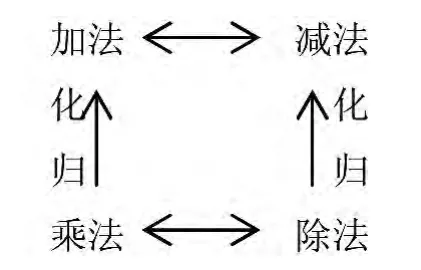
图1 除法与一次化归

从四则运算的起源和发展过程来看，乘法起源于加法。从运算的角度来看，加减是互逆的，乘除也是互逆的。图1 中显示，加减与乘除之间的关系在结构上存在一定的对应关系和类比关系。这种类比关系正是采用映射化归的重要依据。根据映射关系，既然乘法可以化归为加法，那么除法也应该能够化归为减法。经过这样的化归，四则运算之间从整体上体现出逻辑上的自洽性，图1也因此而显得整饬、闭合。

为了更好地理解除法化归为减法，以十进制数的原码运算来说明。

解:

由于是用十进制数举例说明的，因此这里没有特别地显示存储被除数的寄存器的左移位现象，同时也没有显示二进制数除法运算过程中的恢复余数现象。例4 也是这样处理的。

试商(或者估商)是判断被除数(或是中间过程中的余数)是不是够减的过程。在计算机的运算过程中，只会出现0 和1，这里的商4，不是一次性得到的，而是通过4 次减法运算逐步得到的。

3 四则运算的二次化归:除法化归为加法

除法的二次化归的目标和路径如图2 所示。在二次化归中，除法将化归为加法。它是基于减法化归为加法后顺理成章地实现的。为什么会出现这个问题呢?原来这是适应计算机中运算器的运算要求而产生的。

文献［1］中提到:在计算机的运算器中有一个核心部件——加法器，它完成了算术运算和逻辑运算。这就是说，算术运算的四则运算(加减乘除)都是由加法器完成的，四则运算最终都变成了加法运算;减法运算变成加法运算，并不是简单地‘加’一个负数，而是要将数值数据变成补码形式，然后以‘模’运算的方法进行加法运算。

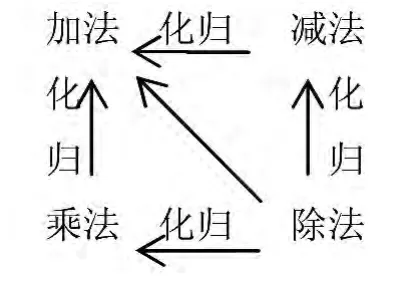
图2 二次化归的目标及路径

“变成补码”正是二次化归的“变形法”的具体体现。它的数学思想是，正数的补码就是它自身，而负数则需要用一个与它等价的正数来代替，从而将减法变成加法。与负数“等价”的正数是什么意思呢?这就涉及到“模”和“同余”的概念了。［6］可以通过下列案例说明。

例2:试用补码计算9 -4 =?

解:因为9 和4 都是个位数，为了使运算最简单、最直观，所以取它们最小的同模10，这时与-4等价的补码是+6，于是

例3:试用补码计算32 -7 =?

解:因为32 的模是100，7 的模是10，同模才能相互加减运算，因此取它们最小的共模100，这时-7 的补码(即等价的正数)是93。

在计算机中，前两步运算早在数据的编译、存储时就已经完成了(计算机中数值数据都是以补码存储的)，最后两步运算，特别是“去模”过程是通过超出模的字长所产生的“溢出”而一次性实现的。之所以采用补码来运算，是因为这样做可以方便地确定减法运算的结果并判断最终的符号。

小学数学教学中没有直接出现“模”的概念，但是存在与之相关的概念，比如“十以内”和“百以内”的加减运算、“单位相同的量”才能进行加减运算等概念，这些概念都是“模”的前概念。

既然减法化归为加法了，那么业已化归为减法的除法，就可以自然而然地化归为加法了。从图2 所示的四则运算的关系来看，除法化归为加法似乎有两条路径:

3.1 路径一：除法-乘法-加法

需注意:(1)数学表达式的每一步变化都伴随着运算意义的变化;(2)示例中的化归，表面上绕过了除法，而实际上显然没有绕过。那个1/3还是要运算的!

3.2 路径二：除法-减法-加法

“除法-减法-加法”的化归路径正是计算机的运算器里实际使用的路径。将除法运算最终化归为加法运算时，计算机中采用了变形法。这里的变形是指负数变成了补码的形式。

在计算机中，数值数据是以补码形式存储的。它是为了避免机器数0 的重码和减法运算的符号判断而提出的优化方案。借助于补码，符号位可以一起参加运算。既然减法变成了加法，对应地，除法运算也就化归为加法运算了。我们可用十进制数的补码运算来说明。

解:取共同的模100，-8 的补码是92，于是

4 结语

以上从数学化归的角度再次研究了除法与四则运算的相互关系。化归思想是数学中的重要思想方法之一，它将复杂问题化归为简单问题，是将复杂运算化归为简单运算，而乘除法运算“化归”为初等的加减法运算后，计算的工作量显然变得繁杂了，这一现象恰恰说明:乘除运算是相同数加减运算的简便运算。

［1］ 张红，张铭.“除法是减法的简便运算”浅说［J］.中小学数学:小学版，2012(5):40 -41.

［2］ 王爱英.计算机组成与结构［M］.北京:清华大学出版社，2001.

［3］ 张铭.计算机与结构中的时间运筹简论［J］.扬州教育学院学报，2008(3):43 -47.

［4］ 张铭.计算机与结构中的空间运筹简论［J］.扬州教育学院学报，2007(3):39 -41.

［5］ 史久一.化归与归纳类比联想［M］.南京:江苏教育出版社，1988.

［6］ 洪修仁. 初等数论［M］. 成都:成都科技大学出版社，1997.