基于ANSYS14.0的数控机床切削加工仿真及关键技术研究

王素粉，秦 冲

(三门峡职业技术学院，河南 三门峡 472000)

随着非线性有限元技术的发展和广泛应用，特别是在数值仿真成功地应用于工程领域之后，一些数值分析已经在切削过程中得到了广泛应用，能够更准确的预测应力、切削温度等一些技术参数，数值分析的核心问题主要是切削形成过程的问题.而近几年，随着自动化程度的发展，智能化数控机床也成为了一种发展趋势，即利用传感器技术对数控机床的加工工艺参数进行自动调整，而在这一技术应用过程中对数控车床切削过程中的一些关键技术参数的分析与实验验证是该技术应用的理论基础，本文利用强大的有限元分析软件ANSYS对数控机床的切削过程进行模拟，不但解决了粘接区的切削分离问题，而且得到了数控机床加工过程中的切削应力变形云图，并预测了切削过程中的切削热、切削力、切削应力的、摩擦力的一些变化曲线，并通过实验验证了实际生产与分析结果的一致性，为进一步数控机床的加工工艺参数的选择与调整打下一定的理论基础，为数控机床的智能化研究提供了一定的研究依据.

1 刀具切削加工有限元模型建立

1.1 几何模型的建立

模型如图1所示，该模型由加工工件、切屑和刀具三部分组成，几何尺寸如下：L1=40mm，L2=2mm，H1=10mm，H2=2mm，H3=9mm，刀具前角α=20°，刀具后角β=5°.工件材料的弹性模量为70GPa，泊松比是0.3，其中屈服应力为400MPa、切线模量为15MPa.刀具选用PLANE182单元类型，弹性模量为210GPa,泊松比是0.3，其应力-应变关系式为[1]9,[2]32-35：Y0=265+180.0ε-0.5.

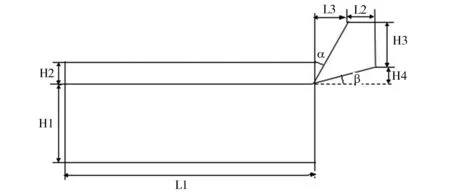
图1 刀具切削加工模型

1.2 摩擦力数学模型的建立

摩擦力数模型如图2所示，根据索瑞夫摩擦理论可以得到，刀具在进行工件切削时候，刀具和切屑的接触面部分可以分为两个部分，如图3所示，也就是粘接区和滑动区，当τf>τmax则位于粘接区，此区域的摩擦系数是不变的，也即是τ=τchip，此时的μi=kchip/σn，而当τf≤τmax时，处于滑动区部分，摩擦力是按照库伦摩擦规律进行的，在计算的过程中，为了能够简化计算过程，根据有限元的特点，引入罚函数，本文把摩擦因数看成是前刀面的正压力函数.其表达式为：

当σ0=kchip/μ时，为摩擦粘接区与滑动区的分界点，也即为库伦摩擦与剪切摩擦的分界点.通过多次的仿真，直至仿真的结果与实测值一致.

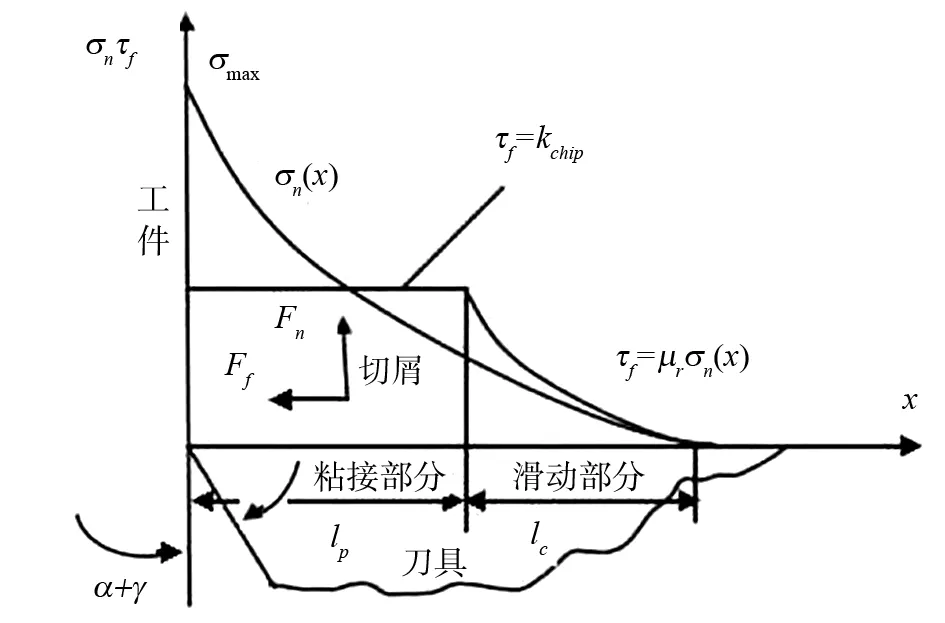
图2 金属切削数学模型

1.2 有限元网格划分

本切削模拟过程中选用单元PLANE182来定义刀具单元类型，使用接触单元CONTA171和TAGGE169定义切屑和金属件之间的粘接，使用接触向导定义刀具与工件及切屑之间的接触，并假设各个接触面的摩擦因数为0.待平面模型建立之后进行网格划分，其中，把工件部分划分成700个单元，刀具划分成16个单元，约束部分为整个工件的底面部分，对于刀具的约束主要是Y向自由度，并且对刀具施加沿着刀具向左向的载荷.刀具切削的有元模型网格划分结果如图3所示。

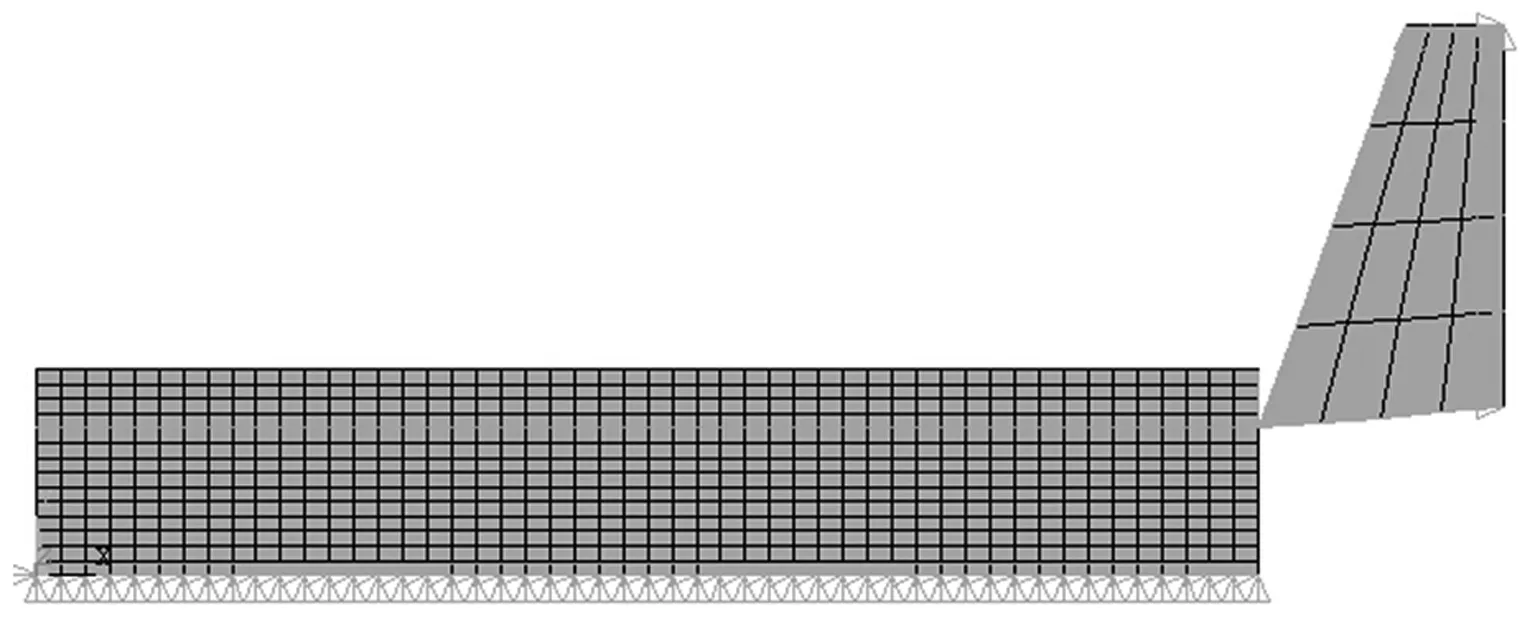
图3 刀具切削模型网格划分

3 刀具切削加工模拟仿真与分析

通过文中1部分模型建立后，定义加载求解，在求解之前控制输出计算结果、设置计算时间和子步，子步为600，载荷加载方式为斜坡加载，并设置自动时间步，激活预测器进行计算处理，计算结束后，提取第10步、30步、60步、100步、200步、235步的子步等效应力云图，并对其温度、切削力进行预测分析.

3.1 切削应力仿真与分析

从图4中的(a)、(b)、(c)、(d)、(e)、(f)6个图中可以看出粘接区模型可以很好地模拟刀具与切屑的分离现象，并且最大等效应力发生在与刀尖相接处的切屑处，最大为472MP.从子步200和子步235可以看出，刀具的后刀面颜色较重，是磨损严重区，当切削过程中，从材料发生塑性变形开始，进入稳定的切削阶段，等效应力基本保持不变[3]248-260.

3.2 切削温度分析

虽然有很多数学计算方式来预测切削中的平均温度变化情况，但是都不能很精确的来预算，而ANSYS14.0有限元分析软件却能较为准确的预测切削温度，在ANSYS14.0有限元软件中，不但能够模拟切屑在流动过程中的应力分布，还能预测刀具切削温度的变化情况，对刀具在切削过程中的磨损以及失效等方面的研究和控制提供了有效的理论参考价值.

3.3.1 加工工件切削温度有限元分析

本文在已经加工好的工件表面进行研究，得出加工表面温度-时间曲线，分别选择的点有节点46、节点50、节点55，如图5所示，通过对图6的切削热传导过程可以发现：在前刀面切屑保持不变时，切削温度还在不断的增加.除此之外，还对其已经加工好的表面的X、Y方向进行了温度变化-时间分析，得出其变化关系，如图7、8所示，通过对图7和图8的分析可以得到，在已加工表面上，X、Y方向的温度变化也是不同的，并且在Y方向的温度变化要比X方向的温度变化明显，从而可以说明在切削过程中的温度扩散量最大的是在垂直于加工表面的方向上.因此，在利用有限元软件进行切削模型简化的时候可以把X方向的温度变化简化为0,这种思想和结论为数控机床金属切削的有限元进一步分析提供了一定的理论基础.

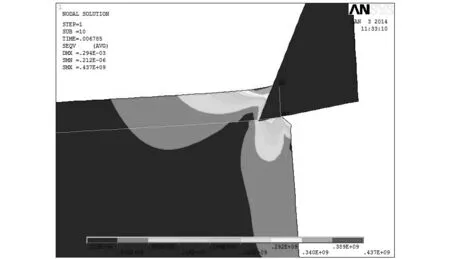
(a)子步为10时的等效应力云图

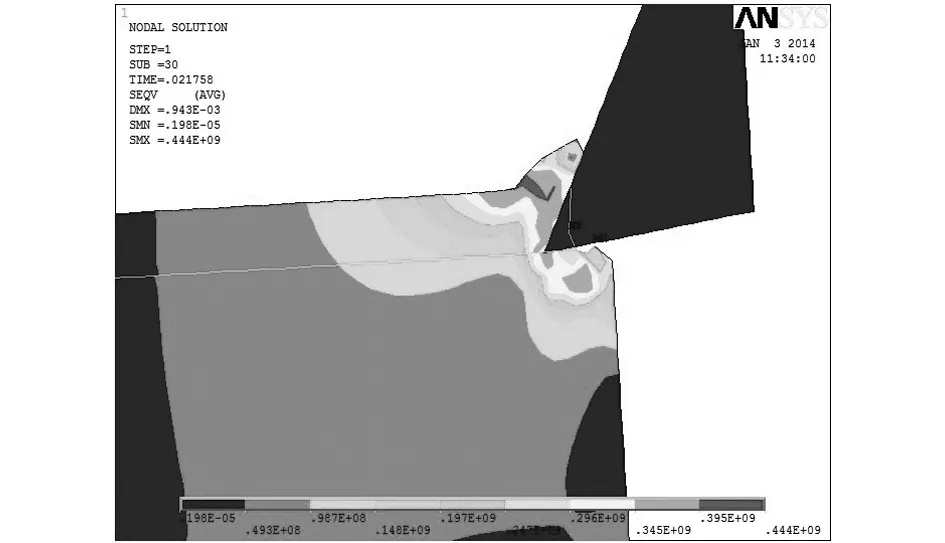
(b)子步为30时的等效应力云图

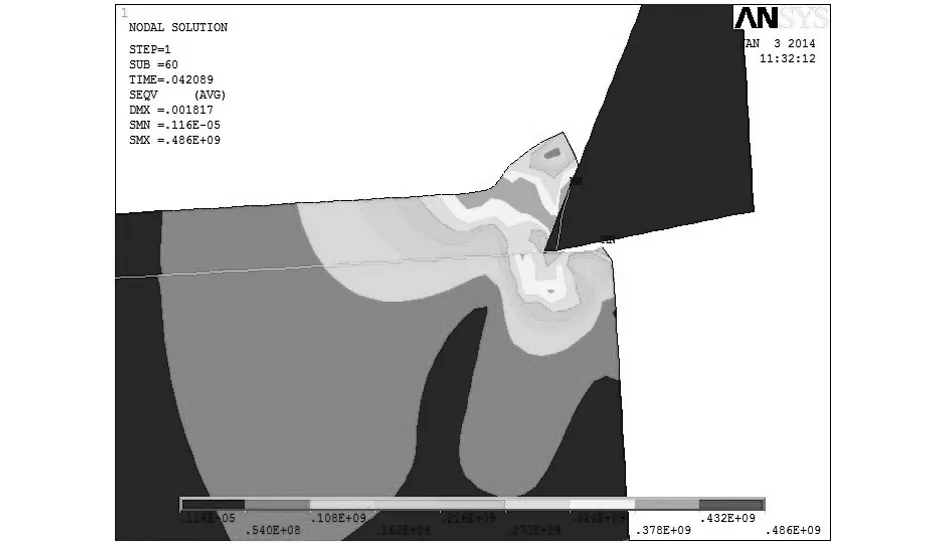
(c)子步为60时的等效应力云图

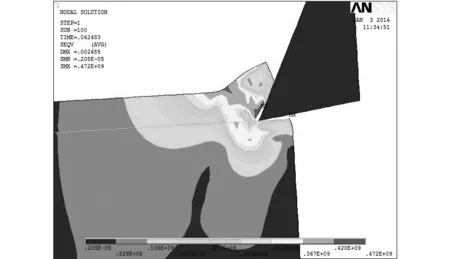
(d)子步为100时的等效应力云图

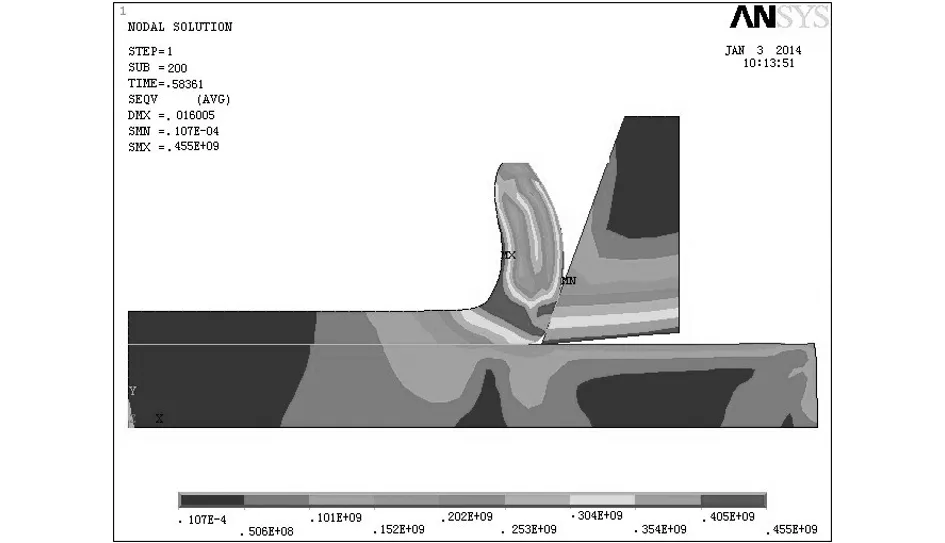
(e)子步为200时的等效应力云图

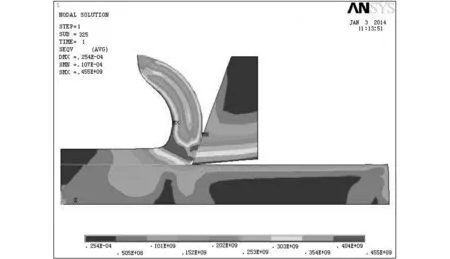
(f)子步为325时的等效应力云图

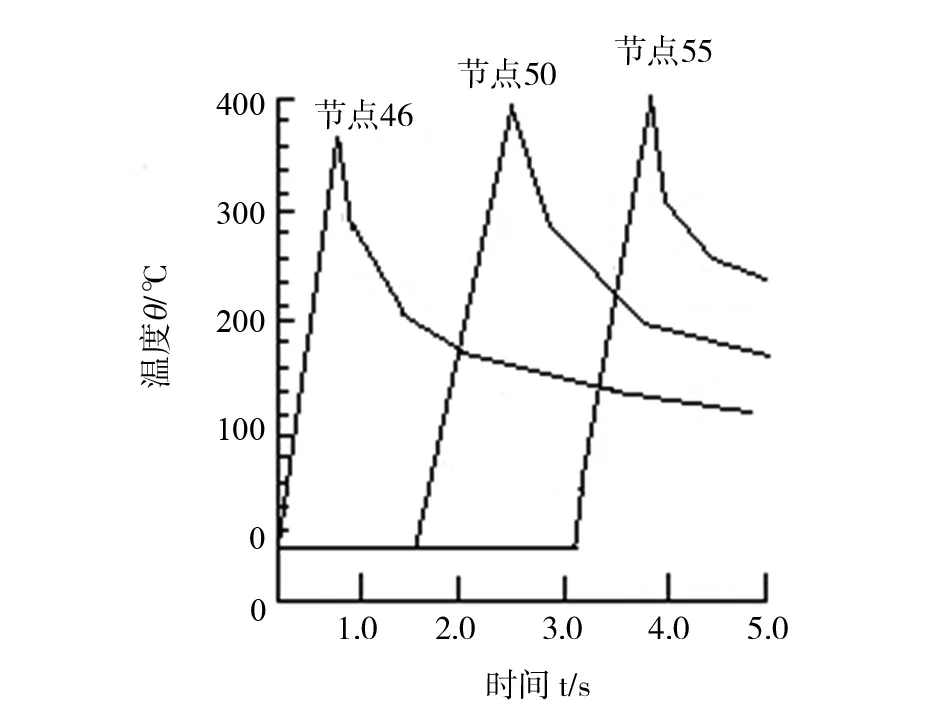
图5 已加工表面温度θ/时间t变化曲线图

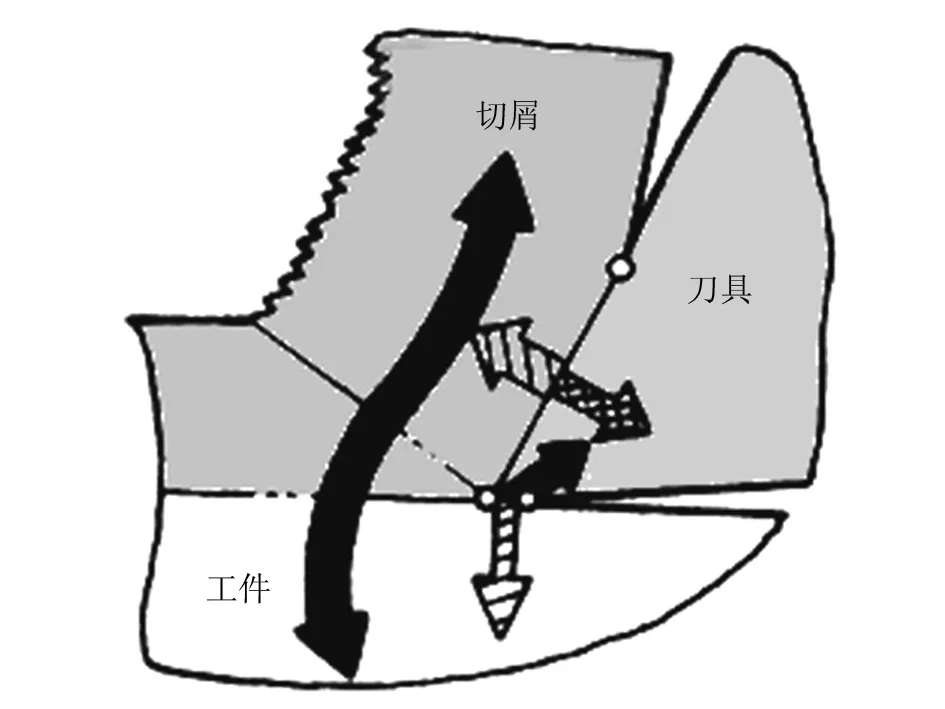
图6 切削加工热量的产生和传导

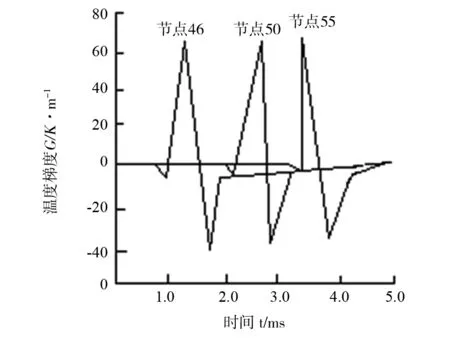
图7 已加工表面在X向温度梯度变化曲线

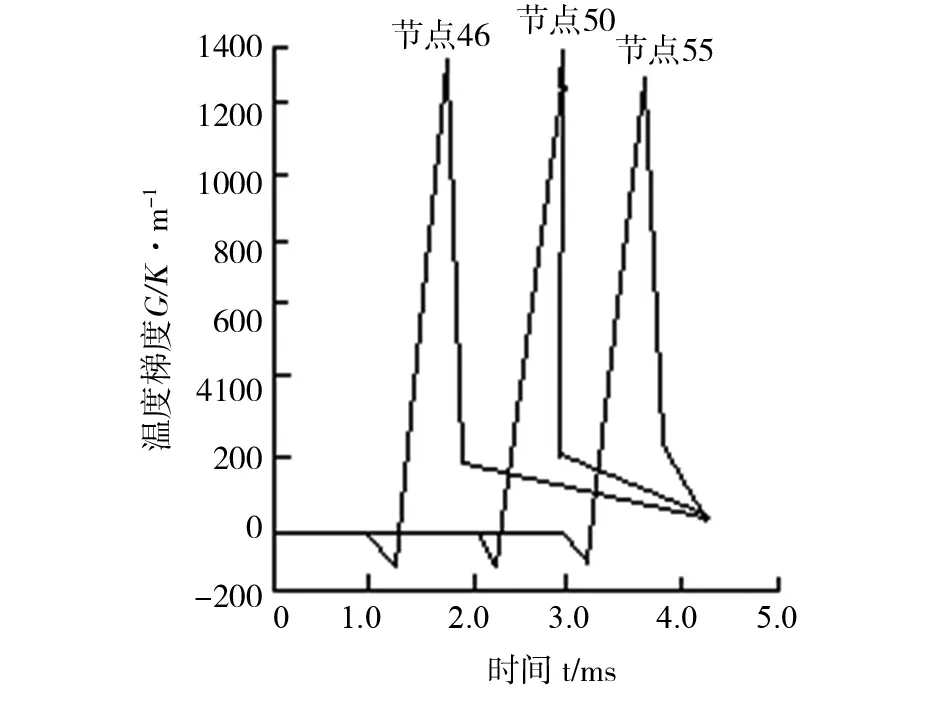
图8 已加工表面在Y向温度梯度变化曲线

3.3.2 切削温度实验与分析

为便于对机床切削过程中温度的变化研究，本文利用热电偶自测传感器建立刀具、工件温度检测系统，通过热电偶传感器感知的到并利用此传感器的进行温度感知与测量，传感器得到的信号经过采集与放大后，通数据传输传给计算机系统，通过改变不同的技术参数得出温度变化与参数之间的关系，便于数控机床工艺的进一步智能化研究.见图9.

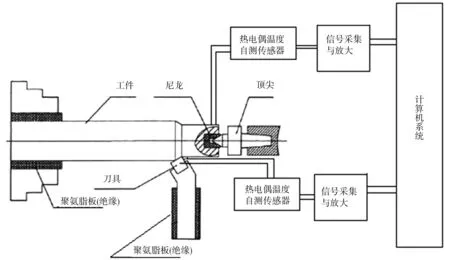
图9 金属切削温度测试系统

从表1中可以看出，前刀面的温度变化随着切削速度的增加而升高，并且测得的温度值与ANSYS仿真值基本一致，此外，分别保持切削速度、进给量不变，改变切削深度和保证切削速度、切削深度不变，改变进给量，对刀具的前刀面进行实际测量温度分析及实际测量温度与仿真值对比，通过分析可以发现：传感器实际测量温度与仿真温度值基本保持一致，前刀面实际温度随着切削速度、切削深度、进给量的增加而增加.这些数据的得出为刀具切削过程的参数控制与智能化研究提供了一定的理论依据.

表1 同一刀具在不同的参数下的热电偶切削温度测量结果

3.3 切削力分析与实验研究

3.3.1 切削力有限元分析

为了分析切削力的变化情况，本文在ANSYS中提取了切削力的变化曲线，分别是进给抗力变化曲线、主切削力变化曲线、切深抗力变化曲线，如图10所示：

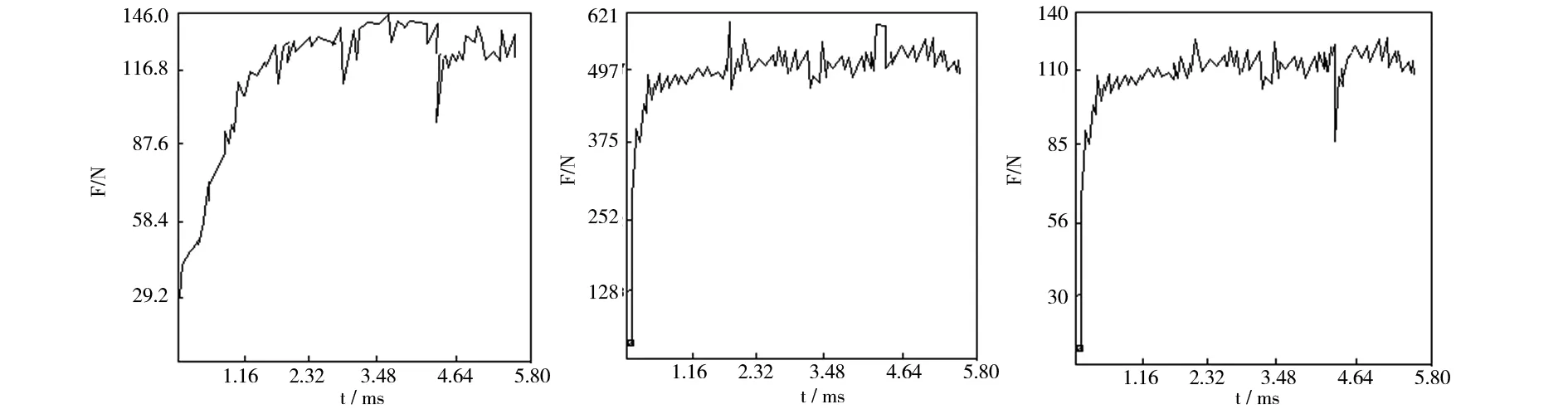
(a)进给抗力变化曲线 (b)主切削力变化曲线 (c)切深抗力变化曲线图10 切削力变化曲线

根据图10结合实际切削过程，可以发现，当刀具刚切入工件的时候，工件发生的是塑性变形阶段，摩擦力是不断增加，从而切削力也呈现不断增大的趋势，然而，当切屑进入成型阶段，切削力逐渐稳定.

3.3.2 切削力实验与分析

为了验证有限元仿真切削力的仿真结果的正确性，本文也对切削过程切削力的测试进行了实验与分析，实验选择的是硬质合金刀具与45#钢工件进行实验研究，并利用压电式三向动态测量仪进行测量，经电荷放大器放大信号后，把信号通过数据线与计算机进行相连，采集信息，得到的信息进行回归分析获得了一些切削用量和技术参数对切削力的影响情况，并经过实验值与仿真值进行对比.其测量结果如图11所示[4]28-33：

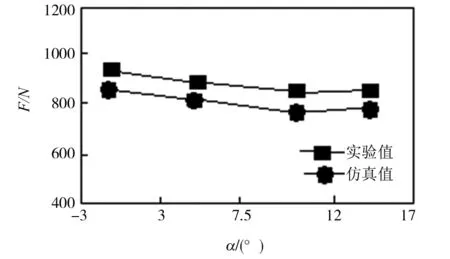
(a)前角对主切削力的影响曲线

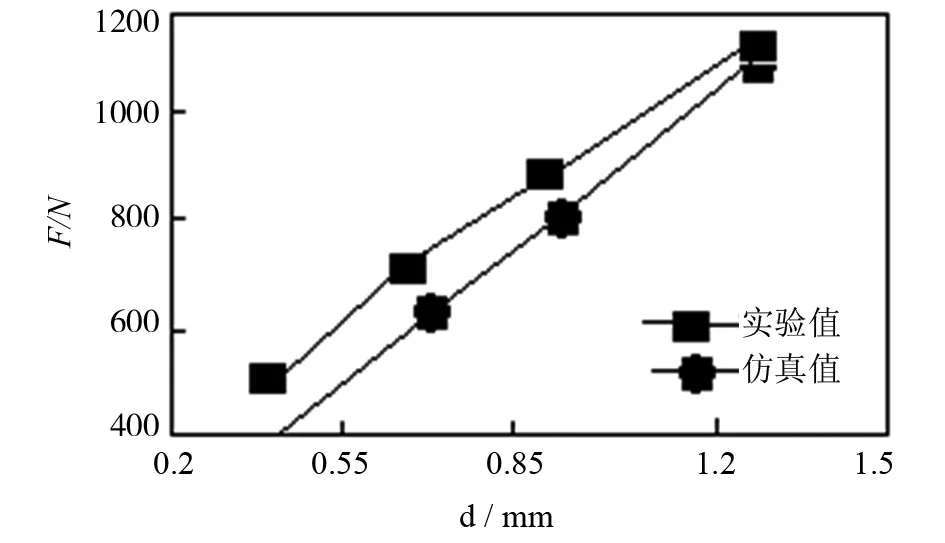
(b)切削深度对主切削力的影响曲线

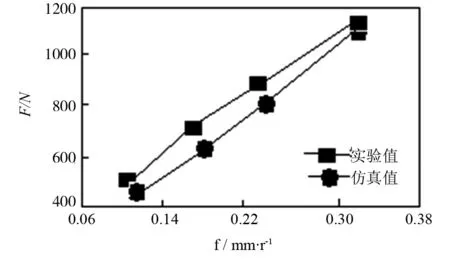
(c)进给量影响下的主切削力变化曲线

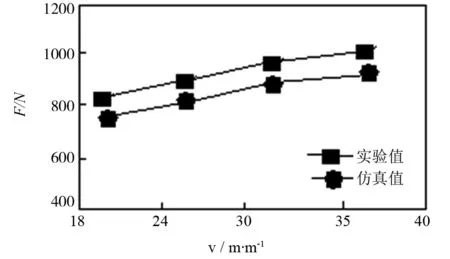
(d)切削速度影响下的主切削力变化曲线

通过图11的实验数值与仿真数值对比可以发现，实验数值与仿真数值基本一致，最大误差不超过19%，并且从图11也可以发现，随着刀具前角的降低、各切削参数的增大，主切削力呈上升趋势.这对数控机床切削过程中的工艺研究提供了理论依据.

4 结语

本文首先利用有限元仿真软件ANSYS14.0对CK6140数控车床刀具切削过程进行仿真，并得出子步应力云图，可以分析最大切削应力发生在与刀尖相接处的切屑处，还通过本软件得出的结论对刀具切削力、切削温度等进行的分析和预测，为了验证刀具温度影响因素、切削力影响因素，本文还引入了传感器技术进行实验研究与分析，通过对切削深度、切削用量、切削速度、刀具前角等参数的变化得出了其对切削温度及切削力的影响规律，并结合仿真值进行对比，得到的结果是两者基本吻合，这些都为数控机床的切削工艺优化及智能化系统的建立提供了一定的理论依据.

[1] 朱江新.切削-挤压成形过程分析与建模方法研究[D].西安:西安理工大学,2006.

[2] 朱江新.基于ANSYS的金属切削过程模拟[J].制造业自动化，2010(11).

[3] 张洪才.ANSYS14.0工程实例解析与常见问题解答[M].北京：机械工业出版社,2013.

[4] 李初晔.金属切削过程有限元模拟[J].航空制造技术，2010(22).