超AKNS方程族和AKNS方程族的一致性探究

牛华伟，白二彪

(1.平顶山教育学院 数学系,河南 平顶山 467000； 2.郑州大学 数学系，河南 郑州 450001)

在研究发展方程对称的过程中，人们发现在物理中提炼出来的非线性发展方程及其所属的方程族(例如KdV[1]1-7，[2]51-57和AKNS[3]，[4]方程族)都有无穷多对称这样的一个共性.由此，人们认为发展方程具有无穷多对称是方程可积的一个特征.如此推来，关于发展方程对称的研究必将推动代数几何中发展方程可积性质的发展，也正是基于这样的原因，对称的研究得到了相当的重视.通过研究人们发现，可积发展方程同时具有K对称和τ对称，并且这些K对称和τ对称通常还能构成一个向量场Lie代数的Lie子代数,他们具有简洁的统一形式.人们进一步认识到对称与发展方程具有深层次的联系.在孤立子发展方程蓬勃发展的过程各种研究对象及其讨论的范围得到了大力的扩充，其中超空间超变量是其中的一方面，超空间是欧式空间的一种推广，包含两种变量，这两种变量分别刻画了量子力学中的波色子和费米子的性质，这个研究方向创世于上世纪中叶，后来形成了超对称理论.经过几十年的发展，形成了寻找方程的对称并构建其Lie代数结构的理论体系.理论研究中大部分只研究一般方程的对称，或只研究超方程的性质而没有将两者结合起来.本文正是基于这种情形，研究了超AKNS方程族和AKNS方程族的对称及其Lie代数结构，发现他们的一致性[1]1-7,[2]51-57,[3]15，[4]4.

考虑如下3×3的Lax对的特征值问题：

其中ξ是一个特征参数，q,r,α,β,A,B,C,ρ,δ是变量x,t的函数.其中函数q,r, A,B,C是偶的，α,β,ρ,δ是奇的.通过相容性原理，可以得到超AKNS方程族：

其中

定理2 超AKNS方程族的方程ut=φnKo，l=0,1,2,…有对称：

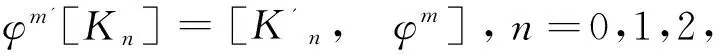
(Ⅱ)φm'[τln]=[τl'n,φm]+mφm+n-1，n=0，1，2，….，m=0,1,2,…，

定理3 超AKNS方程族(2)的对称(5)构成一个Lie代数：

[Km,Kn]=0，

[Km,τln]=mKm+n-1，

[τlm,τln]=(m-n)τlm+n-1，

l=1，2，3，…,m,n=0,1,2,…，

当取2×2的Lax对:

相应可得到AKNS方程族：

其中

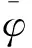
l=1，2，3，…,m,n=0,1,2,…

通过上面的讨论可以发现，超变量的引入没有影响超AKNS方程族对称及其Li代数结构的讨论，从而超AKNS方程族和AKNS方程族的对称和Lie代数结构在形式上是一致的.

[1] 王宝勤，张飞军.源于KdV方程的延拓结构的方程与对称[J].新疆师范大学学报(自然科学版)，1998,17(02).

[2] 斯仁道吉尔.组合KdV方程的强对称、对称及其Lie代数[J].内蒙古师大学报(自然科学汉文版)，1992,(s1).

[3] 陈守婷.半离散AKNS系统的对称及代数结构[D].上海：上海大学，2011.

[4] 袁洪芬.超空间上Dirac型方程解的性质[D].石家庄：河北师范大学，2012.