基于BP神经网络的磁罗盘误差补偿研究

邵婷婷,樊延虎,吕浩北,郭 娜

（延安大学 物理与电子信息学院，陕西 延安 716000）

磁罗盘是利用地磁场来实现定向功能的装置，广泛应用在航空、航海、车载定位、地质勘探、深海探测等领域[1]。随着微处理器技术的发展，尤其是单片机技术的广泛应用，结合利用先进加工工艺生产的磁阻传感器，为导航系统的数字化提供了有利的帮助，是未来磁罗盘的发展方向[2]。本文基于磁阻传感器HMC1052/1051Z和MEMS加速度计ADXL203研制了一款磁罗盘样机，分析了样机工作过程中可能存在的误差及其来源，建立了以测量航向角为输入、补偿后的航向角为输出的三层BP神经网络模型，经该算法补偿后的样机航向角精度可提高至±0.50以内。

1 测量原理与误差分析

本文研制的磁罗盘框图如图1所示。该系统主要基于磁阻效应，根据磁场大小来确定方向。

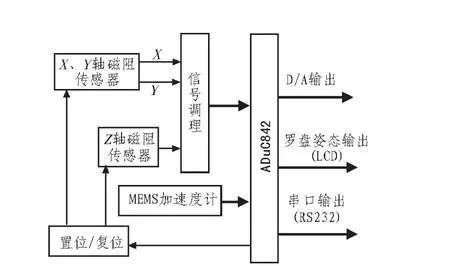
图1 磁罗盘结构框图Fig.1 Assumption diagram of magnetic compass

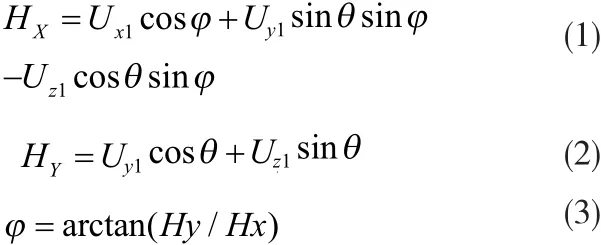
MC1052/HMC1051Z分别感测载体坐标系下地球磁场X、Y、Z轴的分量 Ux1,Uy1,Uz1，MEMS加速度计ADXL203通过感知地球重力加速度在其测量轴上的分量大小而确定俯仰角φ和翻滚角θ，根据理论公式(1)、(2)[3]，可求得折算到地平坐标系中相同航向下地磁场在X轴和Y轴的分量Hx和Hy，则航向角φ可根据公式(3)求得。据罗盘坐标系和水平坐标系变换的分析以及样机的实际运行情况，根据文献[4]介绍的方法对航向角作相应的处理，使之能在00～3600的范围表示。

磁罗盘的误差主要可以分为两类[5]：第一类是系统自身存在的误差，包括制造误差、安装误差，该部分对系统精度影响较小；第二类是由磁罗盘周围工作环境因素造成的误差，主要指罗差，罗差对电子罗盘系统的精度影响最大，可达几十度。本文在软件上首先采用中值滤波算法对数据进行预处理，基于BP神经网络，建立以测量航向角为输入、补偿后的航向角为输出的三层BP神经网络模型，对误差进行补偿校正。

2 BP神经网络误差补偿模型建立

2.1 BP神经网络

前馈神经网络是一种基于监督学习的人工神经网络，它能够通过学习已知样本而掌握经验，从而对未知样本做出判别，适合于曲线拟合、模式识别等领域[6]。BP神经网络是一种多层的前馈型神经网络，一般包括一个输入层、若干个隐层和一个输出层。BP网络采用梯度下降的误差反向传播算法对样本进行训练[7]，网络训练分为批处理模式和递增模式，本文采用的是批处理模式。

2.2 误差模型的建立

对设计的样机在水平状态时，航向角从00～3600每隔150共24个实验点获取训练样本，未经补偿的航向角误差在00～3600近似于正弦曲线，且绝对值最大可达三十几度，如图2所示。本文以此为训练样本，利用MATLAB 神经网络工具箱进行BP神经网络模型的建立。并采用贝叶斯归一化学习算法训练网络，以确定网络参数。

图2 航向角样本误差图Fig.2 Magnetic course angle sampling error diagram

1)BP神经网络结构的确定

数学上已经证明了BP神经网络可实现任何复杂的非线性映射，理论上，一个三层的神经网络，能够以任意精度逼近给定的函数[8]。本文采用以测量航向角为输入、补偿后的航向角为输出的三层BP神经网络结构，隐含层传输函数采用S型函数logsig，输出层传输函数采用线性函数purelin。

2)输入、输出量的处理

在工程领域中，使用BP神经网络好坏的关键是输入量训练样本的优劣，为提高训练样本集的代表性，加快网络训练的收敛性，本文将输入的实测航向角用公式(4)做了归一化处理，使航向角训练样本能够集中在区间[-1，1]中。

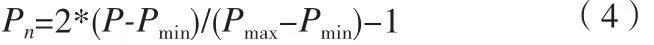
式中，Pn为归一化后的航向角测量值，Pmax，Pmin为测量值的最大值和最小值，P为航向角的原始测量值。训练后对输出量采用公式(5)作反归一化处理。

3)隐层神经元个数的确定

隐层神经元个数的确定是BP神经网络模型建立的关键技术之一，可根据+（0～10）来确定。本文输入层和输出层节点数均为1，经过不同隐层神经元个数的尝试，本文最终确定网络的隐层神经元个数为6。

3 仿真实验及结果分析

网络模型建立并训练完毕之后，让样机在水平状态下，航向角从 每隔 共24个实验点再测得一组航向角，将该数据作为建好的BP网络模型的输入，经仿真后得到补偿后的航向角。表1为磁罗盘样机采用该BP神经网络算法，误差补偿前后的航向角和误差。

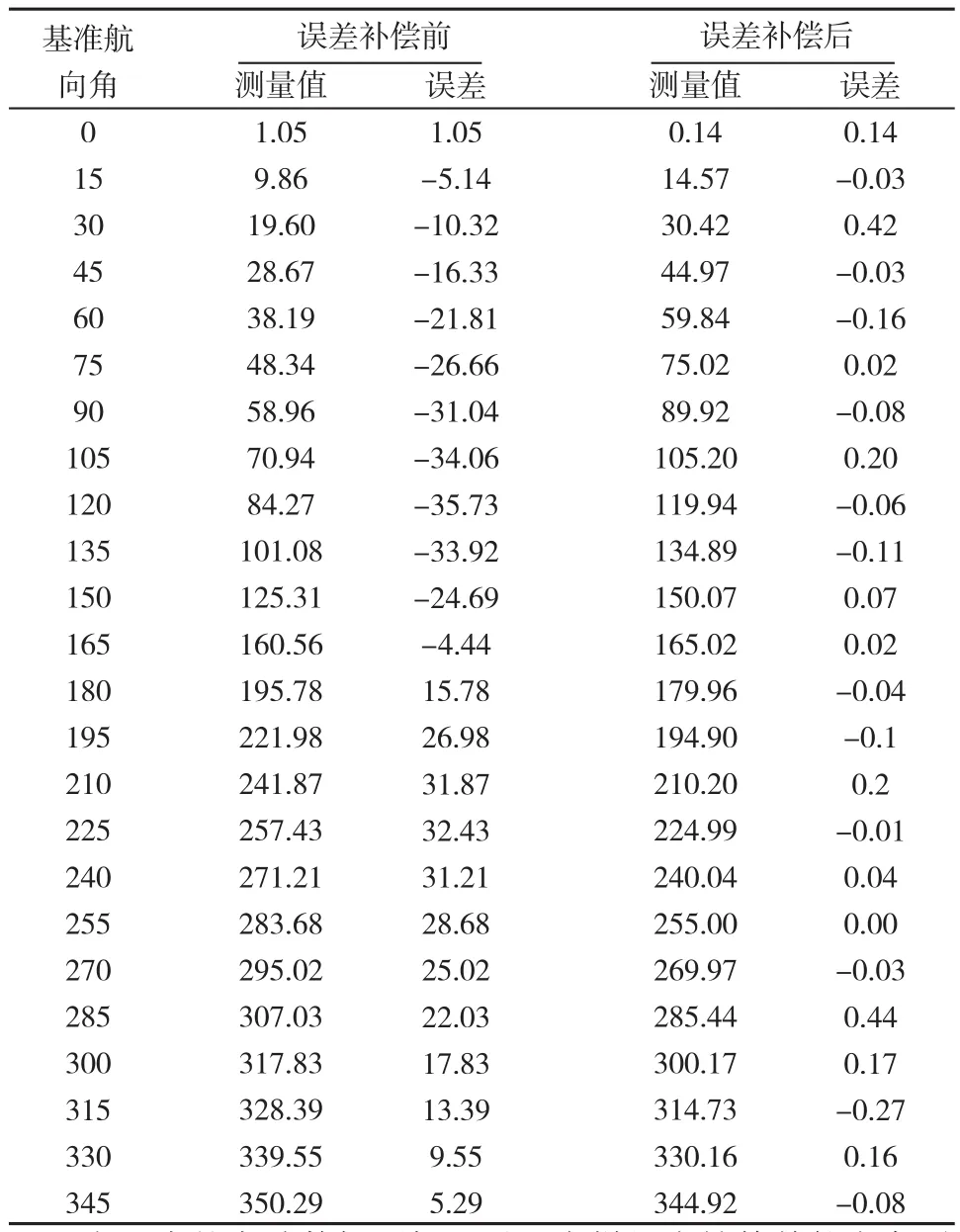
表1 航向角测量数据Tab .1 Course angle measurement data

由上表的实验数据可知，磁罗盘样机在补偿前航向角误差最大可达±35.73°，经过该BP神经网络算法补偿后航向角误差大大减小，实验点的航向角误差均在±0.5°以内。

4 结束语

基于磁阻传感器HMC1052/1051Z和MEMS加速度传感器ADXL203研制的磁罗盘样机，系统成本低、体积小、功耗低。利用地球磁场测量航向，易受外界磁场干扰，利用前馈神经网络算法，建立了以测量航向角为输入、补偿后的航向角为输出的三层BP神经网络模型，并用样机的采样数据进行仿真验证，实验证明，该BP神经网络误差补偿仿真稳定，补偿效果好，航向角精度可提高至±0.5°以内，研制的样机可应用于普通导航领域。

[1] Vcelak J , Ripka P , Kubik J , Platil A , Kaspar P. AMR Navi2gation Systems and Met hods of Their Calibration[J ] . Sensors and Actuators 2005 ,1222128.

[2]王勇军, 李智, 李翔. 三轴电子罗盘的设计与误差校正[J].传感器与微系统, 2010, 29(10): 110-112.WANG Yong-jun, LI Zhi, LI Xiang. Design and error calibration of three-axis electronic compass [J]. Transducer and Microsystem Technologies, 2010, 29(10): 110-112.

[3] 金海红, 吴东升, 田柳. 倾斜补偿式地磁传感器的设计与误差补偿方法[J]. 传感器与微系统, 2010, 29(10): 33-36.JIN Hai-hong, WU Dong-sheng, TIAN Liu. Design and error compensation method of tilt compensated earth magnetism sensor [J].Transducerand Microsystem Technologies, 2010, 29(10): 33-36.

[4]邵婷婷,马建仓,胡士峰,等.电子罗盘的倾斜及罗差补偿算法研究[J].传感技术学报,2007, 20(6)：1335-1337.SHAO Ting-ting, MA Jian-cang, HU Shi-feng. Research ontilt and environment error compensation based on electronic compass[J]. Chinese Journal of Sensors and Actuators, 2007, 20(6): 1335-1337.

[5] 马建仓, 胡士峰, 邵婷婷. 三轴磁阻电子罗盘设计[J]. 火力与指挥控制, 2009, 34(3): 142-144.MA Jian-cang, HU Shi-feng, SHAO Ting-ting ,et al. Design of A 3-axes magnetoresistive electronic compass [J]. Fire Control and command control, 2009, 34(3): 142-144.

[6]曲建岭, 高峰, 李富荣,等. 基于人工神经网络的磁航向误差校正方法[J]. 计测技术, 2006, 26(3): 8-9.QU Jian-ling, GAO Feng, LI Fu-rong ,et al. Error revising method for magnetic course based on artificial neural network [J].Metrology& Measurement Technology, 2006, 26(3): 8-9.

[7]王璐, 赵忠, 邵玉梅,等. 磁罗盘误差分析及补偿[J]. 传感技术学报,2007, 20(2)：439-441.WANG lu, ZHAO Zhong, SHAO Yu-mei , et al. To analyze and compensate errors of magnetic compass [J]. Chinese Journal of Sensors andActuators, 2007, 20(2): 439-441.

[8] 徐晓东，赵忠,等. 基于BP网络的激光陀螺刻度因子的精确建模[J] . 传感技术学报, 2005, 18 (2) :3982400.XU Xiao-dong, ZHAO Zhong，et al. The accurate modeling of LaserGyro scale factor based on BP network [J]. Chinese Journal of Sensors and Actuators, 2005, 18(2): 398-400.