弧形闸门泄流特性分析

赫振平，王 东

（册田水库管理局，山西大同，037300）

0 引言

水闸是水利水电工程中用来控制水工建筑物泄洪流量的重要设备，其设计计算直接影响到水库等级的确定以及水库正常的兴利调度和调洪运用。在大坝安全事故中,因溢洪道运行不当造成的约占27%，溢洪道容量不足为主要因素的约占22%，因此，闸门的正常运行、可靠度对保证大坝安全起着极其重要的作用。

在水库除险加固泄流能力复核计算中，发现过去应用的“水位-泄量”关系曲线与《水力计算手册》、《溢洪道设计规范》、《水闸设计规范》、水力学计算数据相互之间相差较大，同时正常溢洪道一直沿用建设初期由模型试验结果点绘而成的“水位-泄量”关系曲线，原模型试验以及2010年水库除险加固时重做的水工模型试验均按敞泄设计，未考虑闸门局开时“水位-开度-泄量”三者之间的数学关系。水库正常运用时，小泄量、小开度运用频繁，在防洪调度时，敞泄的情况也不多见，在防洪调度以及其他情况需泄水时,闸门开度多大才能达到相应的泄量、泄量是否准确等问题给水库运行带来一定的不便和盲目性，在水库防洪时存在一定的隐患，因此有必要对闸门的泄流特性进行研究。

1 基本情况

1.1 工程概况

册田水库始建于1958年，位于桑干河中上游，属海河流域永定河水系，总库容5.8亿m3，坝址以上控制流域面积16 700 km2，占下游官厅水库流域面积38.5%，大坝为均质土坝，最大坝高42 m，是一座多年调节的大（2）型水库。水库承担着“21世纪初期首都水资源可持续利用项目”中为北京市输水的任务，是山西省唯一一座全国重点防汛水库。

水库正常溢洪道位于大坝左坝肩，为岸边潜孔式正槽溢洪道，包括闸前防渗段、闸室控制段、泄槽段及挑流鼻坎消能段4部分，全长492.7 m。其中，闸前防渗段长18.0 m，宽38.6 m，底高程为943.3 m；闸室控制段长28.0 m，总宽度38.6 m，设4孔带胸墙的弧形钢闸门泄洪孔口，孔口宽8.0 m、高6.0 m，闸墩厚2.2 m，原设计最大泄量2 490 m3/s，溢流堰为无底坎宽顶堰，堰顶高程943.3 m。

1.2 正常溢洪道泄量数据比较

多种情况下正常溢洪道的水位-泄量关系数据见表1。由表1知，堰流阶段数据较有规律，而在闸孔出流时相互间相差较大（见图1）。

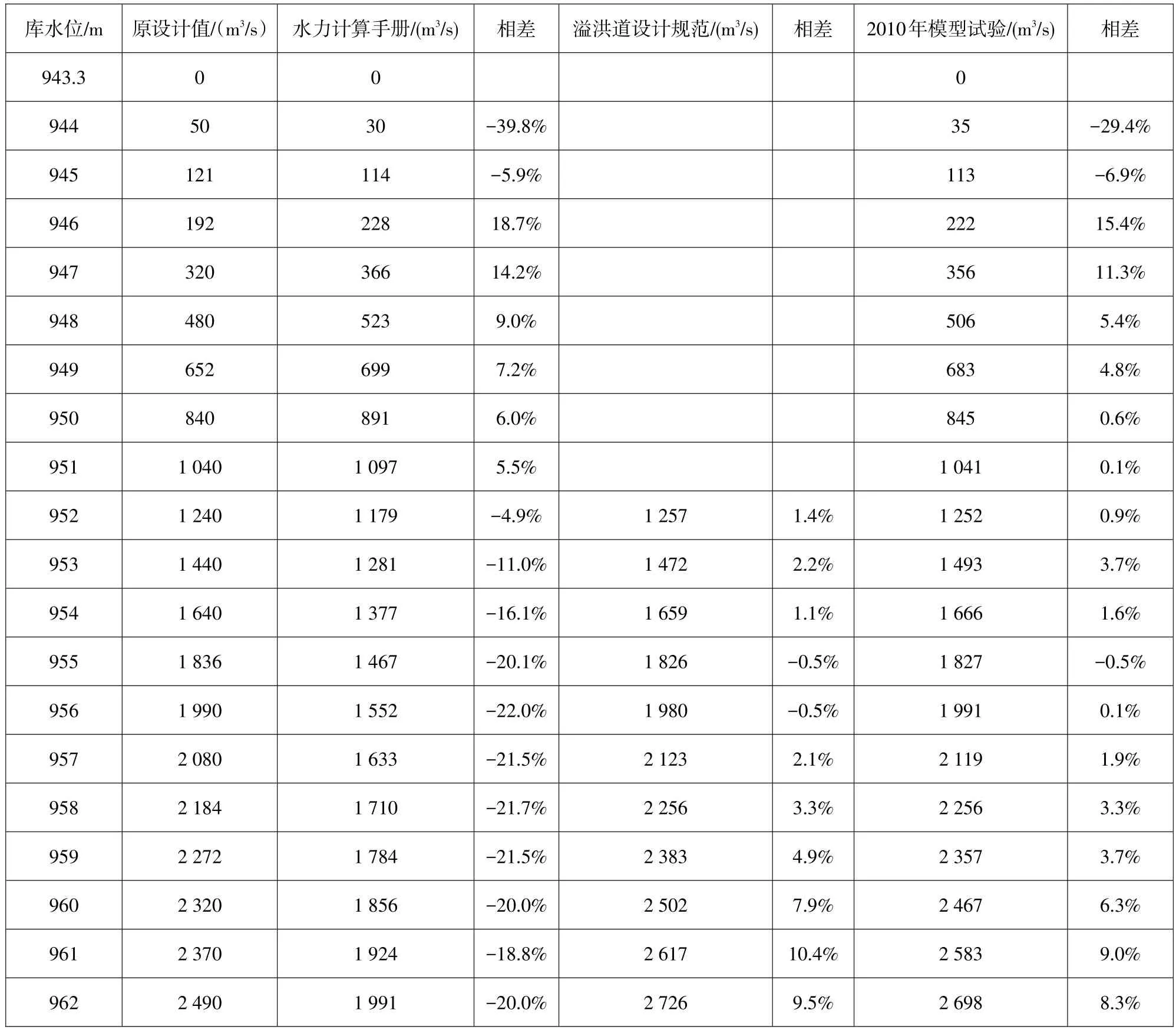
表1 正常溢洪道水位-泄量数据表Table 1 Relation between reservoir level and flow for the normal spillway

表1中原设计值为历年来一直采用数据；2010年模型试验，由于库水位数据比较零散，故在表1中采用了二次回归插值化整，在图1中未做调整；水力计算手册、水力学以及水闸设计规范中弧形闸门流量由能量方程式推求而得，由能量方程式推导出的计算公式基本相同，推导过程在此不再重复。在表1中，堰流时综合流量系数m’采用0.362 5，闸孔自由出流时流量系数μ采用推荐公式求得；溢洪道设计规范中无底坎带胸墙平底宽顶堰闸门在孔流时的计算公式中，流量系数采用推荐值μ＝0.90。

1.2.1 堰流流量的计算公式

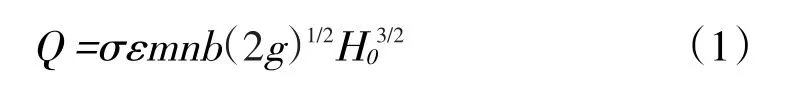
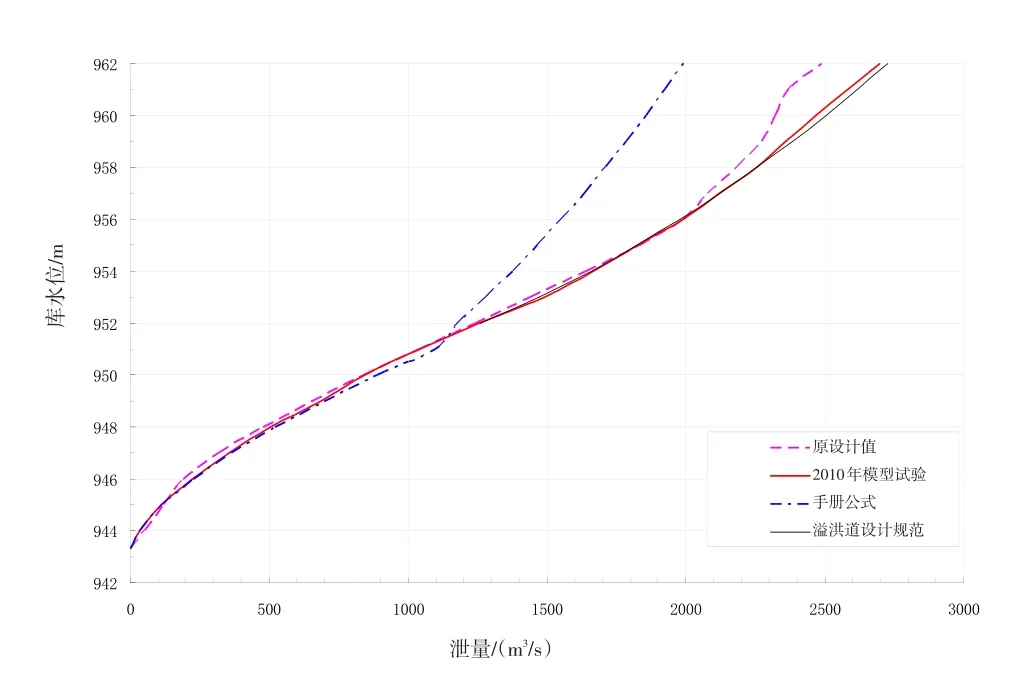
图1 水位-泄量关系曲线图Fig.1 Relation between reservoir level and flow

式中：Q为堰流流量，m3/s；σ为堰流淹没系数，自由出流取1.0；ε为堰流侧收缩系数；m为堰流流量系数；n为闸孔孔数；b为闸孔总净宽，m；g为重力加速度；H0为计入行近流速水头的上游能头，m。

式（1）中，σ、ε可由孔径、堰型、墩型、上下游水位关系等按有关经验公式或相关图表得出，规范中规定堰流流量系数m可取0.385，此值为进口局部能量损失为0时的堰流流量系数值，即最大值。查表后采用综合流量系数m'＝0.362 5。

1.2.2 闸孔出流流量公式

式中：μ为闸孔自由出流流量系数；e为闸门开启高度。式（2）中，对于弧形闸门流量系数μ，可由下式求得：

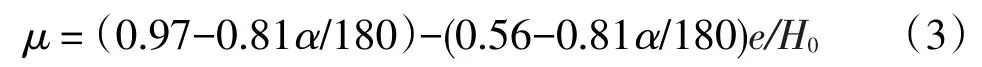
式中：α为闸门下缘切线与水平方向夹角；其他符号同上。

2 数据分析

2.1 堰流时模型数据的选用与公式流量系数的修正

手册、规范与水力学中对于宽顶堰：当e/H≤0.65时，为孔流；e/H＞0.65时，为堰流。在敞泄时对应的库水位为952.53 m。分析时，952～953 m数据暂不考虑，即以库水位小于952 m为堰流，954 m及以上时为闸孔出流。

首先，由原设计和2010年模型流量数据采用式（1）公式反推求得综合流量系数m'（此系数包括了侧向收缩、垂直收缩等有关系数）；然后，采用最小二乘法确定最优综合流量系数并比较模型流量数据的优劣。计算结果见表2。

从表2可知，堰流时2010年模型试验数据较优，此时综合流量系数m'=0.344 8。

2.2 闸孔出流时模型数据的选用与公式流量系数的修正

闸孔出流时应用方法基本同2.1，计算结果见表3。由式（3）可知,闸孔出流时在闸门开启高度不变时，流量系数为相对开度的一次函数，流量系数采用回归分析方法求得，并通过相关指数来比较模型流量数据的优劣。

从表3、图2可知，在闸孔出流时2010年模型试验数据较优，此时综合流量系数μ=0.9198-0.5701e/H，相关指数R2=0.995。

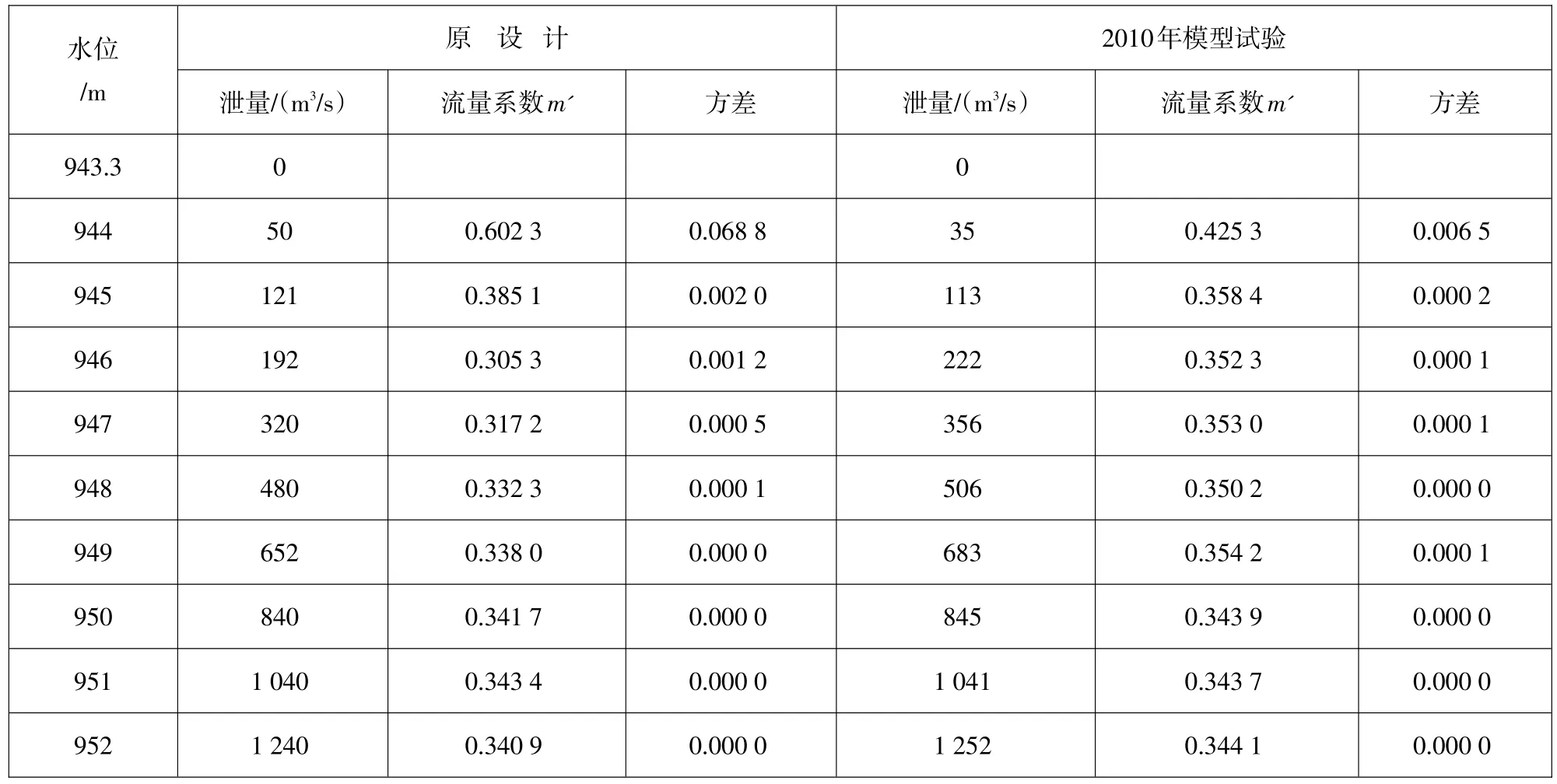
表2 堰流时综合流量系数计算与比较表Table 2 Comparison of the weir flow coefficients in original design and in model test

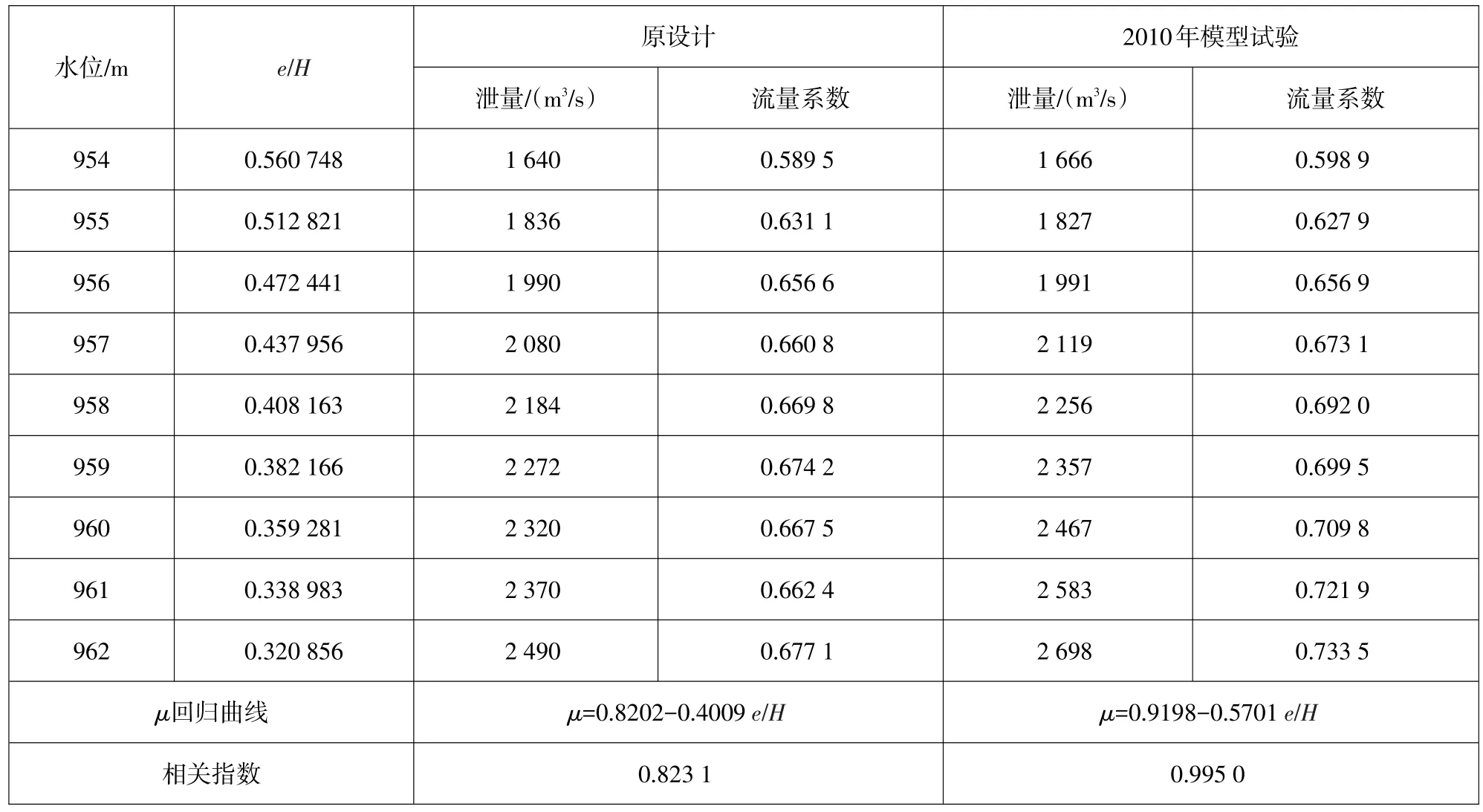
表3 闸孔出流综合流量系数计算与比较表Table 3 Comparison of the orifice flow coefficients in original design and in model test

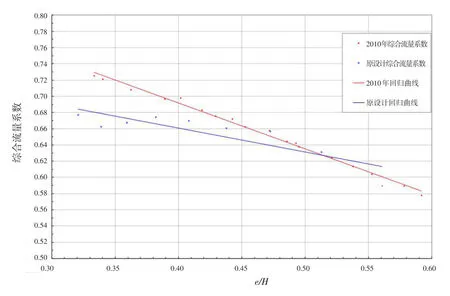
图2 闸孔出流综合流量系数μ-e/H关系图Fig.2 Relation betweenμand e/H as orifice flow

2.3 溢洪道设计规范中带胸墙平底宽顶堰公式精度分析

在溢洪道设计规范中，有专门针对密云水库、册田水库、石山口等水库无底坎带胸墙平底宽顶堰闸门在孔流时的公式：

式中，Q为流量，m3/s；μ为孔口自由出流流量系数，从0.7～0.9不等，圆滑孔口设计时，推荐值μ＝0.90；A为孔口面积，m2；Ho为自闸底板算起的计入行进流速水头的上游总水头，m；D为孔口高度，m。

流量系数采用公式（4）反推求得,计算结果见表4。由表4可知，采用最优流量系数μ＝0.897 4时，公式计算与模型试验流量数据误差多数在1%以内，而μ与推荐值0.90相差不足3‰，说明计算无底坎带胸墙平底宽顶堰闸门在孔流时，应用溢洪道设计规范中的公式（4）有较高的精度。

2.4 堰流与闸孔出流界限的划定

对于宽顶堰来说，堰流与孔流的界限，规范中的界限定为0.65，由此计算敞泄时对应的库水位为952.53 m，在2010年模型试验中，采用953 m作为堰流与孔流界限。

依据优化后的堰流、孔流计算公式以及2010年模型试验数据，计算结果是孔流与堰流的界限e/H=0.592 2，此时对应的库水位为953.431 m，见图3所示，比规范计算的高，这也从一个侧面印证了模型实测数据比理论公式计算数据偏大。

3 不同开度时泄量公式中流量系数的推导

原设计以及2010年的模型试验均未考虑闸门局开时的泄量关系,在不同库水位时，闸门开度多大才能达到防洪或供水要求的泄量、泄量精度是否能满足要求是亟需解决的问题，如果采用手册中闸孔出流公式，由表1数据可知，在敞泄时误差很大，因此，手册中闸孔出流公式不能直接运用。

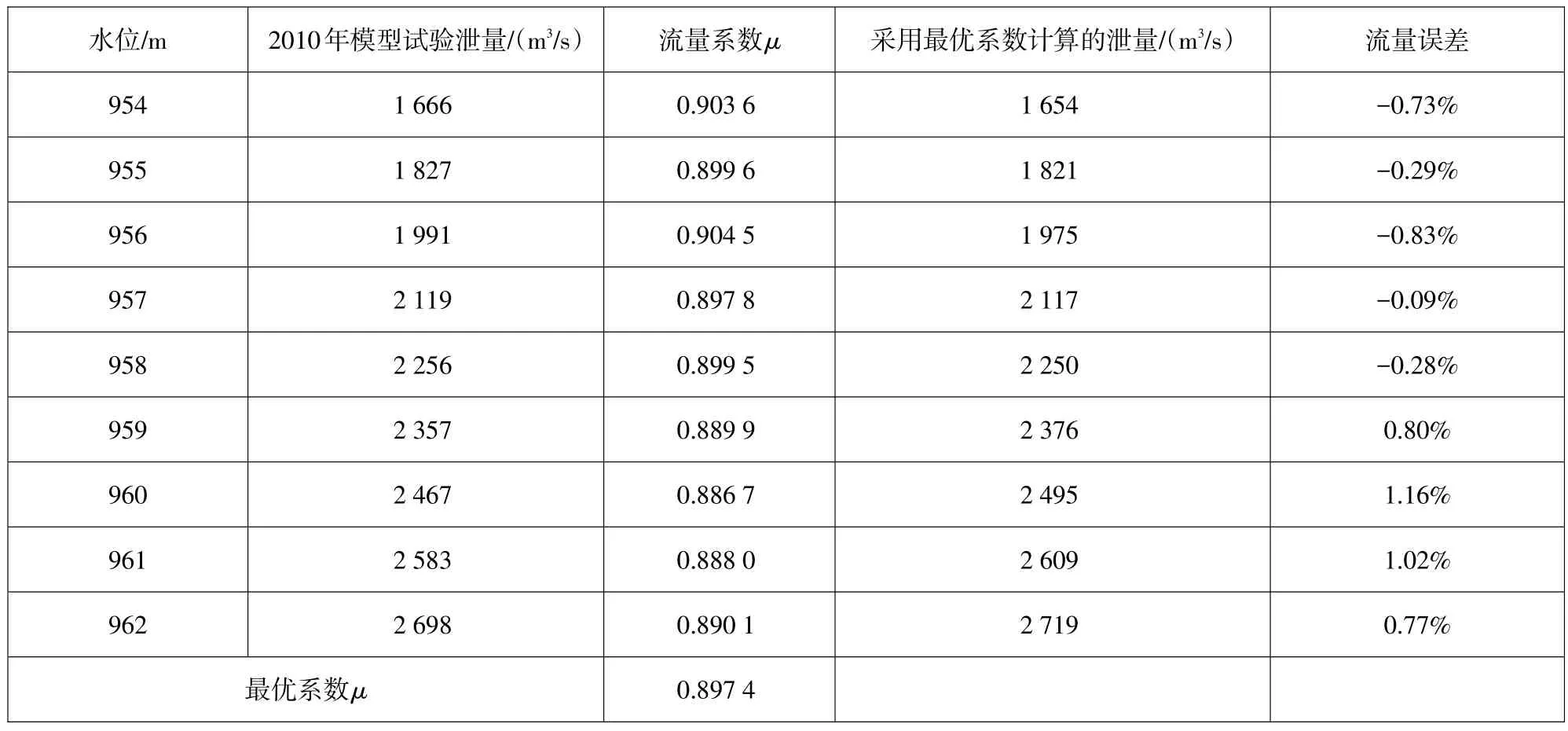
表4 溢洪道设计规范公式与2010年模型试验比较表Table 4 Comparison of the discharge flows calculated by design code for spillway and in the model tests

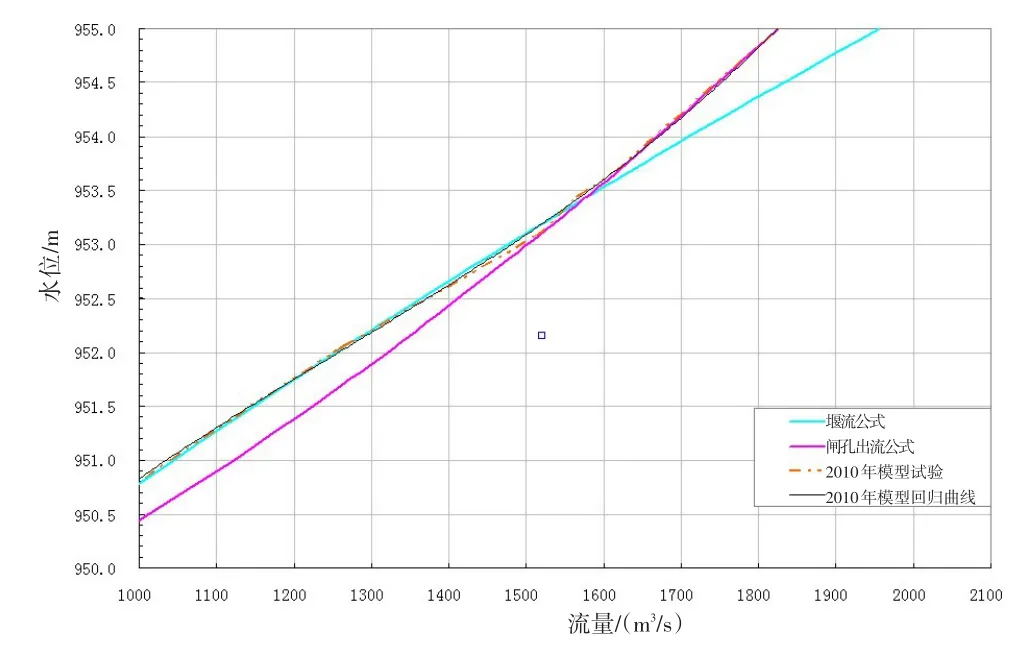
图3 堰流与孔流分析图Fig.3 Comparison between the weir flow and the orifice flow

两者产生较大误差的原因，主要是由于流量系数μ受较多边界条件的影响较大。具体分析认为，闸门的上游左侧导墙在原设计时留有5×5个直径1.2 m的减压孔，泄流时由于左侧导墙内外存在压差，泄流时左侧导墙外的水同步从减压孔流入，因而引起模型实测流量值大于公式计算。

由于模型试验缺少闸门局开时的泄量数据，为了求出闸门不同开度时的流量系数函数关系，现将手册中闸孔出流公式中流量系数公式（3）的形式变换为：

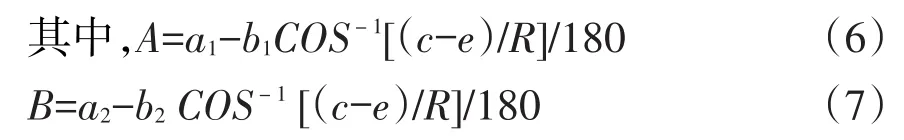
式中，A、B为函数的系数；a1、b1、a2、b2为待定系数；c为闸门门轴高度；e为闸门开高；R为弧门半径。

由式（6）、（7）知，A、B仅是闸门开高e的函数。根据近年来向北京市输水情况可知，库水位为951～949 m、小泄量时（e＜1 m，Q＜100 m3/s）采用手册流量系数推荐公式计算与实测流量误差不大。因此，当e=0 m时，由手册流量系数公式（3）求得流量系数：

μ=0.7837-0.3737e/H，即有A0=0.7837，B0=0.373 7；（A0、B0下标为开高值，下同）。

当e=6m时，采用计算推求的最优流量系数求得：

μ=0.9198-0.5701e/H，即 有A6=0.919 8，B6=0.570 1。

不同开高时A的中间值由下式计算（B值计算相同不再列出）：

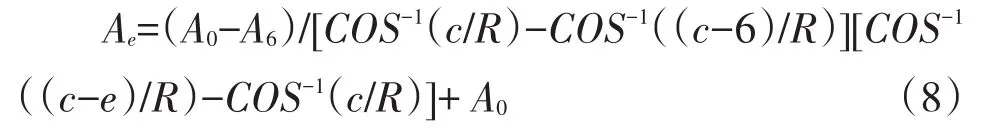
不同开高时A、B取值分布见表5，最后求解出待定系数a1、b1、a2、b2，计算成果见表5（仅列出部分开高e），优化后的流量系数理论关系式为：

由闸孔出流计算公式式（2）和优化后的流量系数关系式（9）计算的水闸部分开高成果见图4。

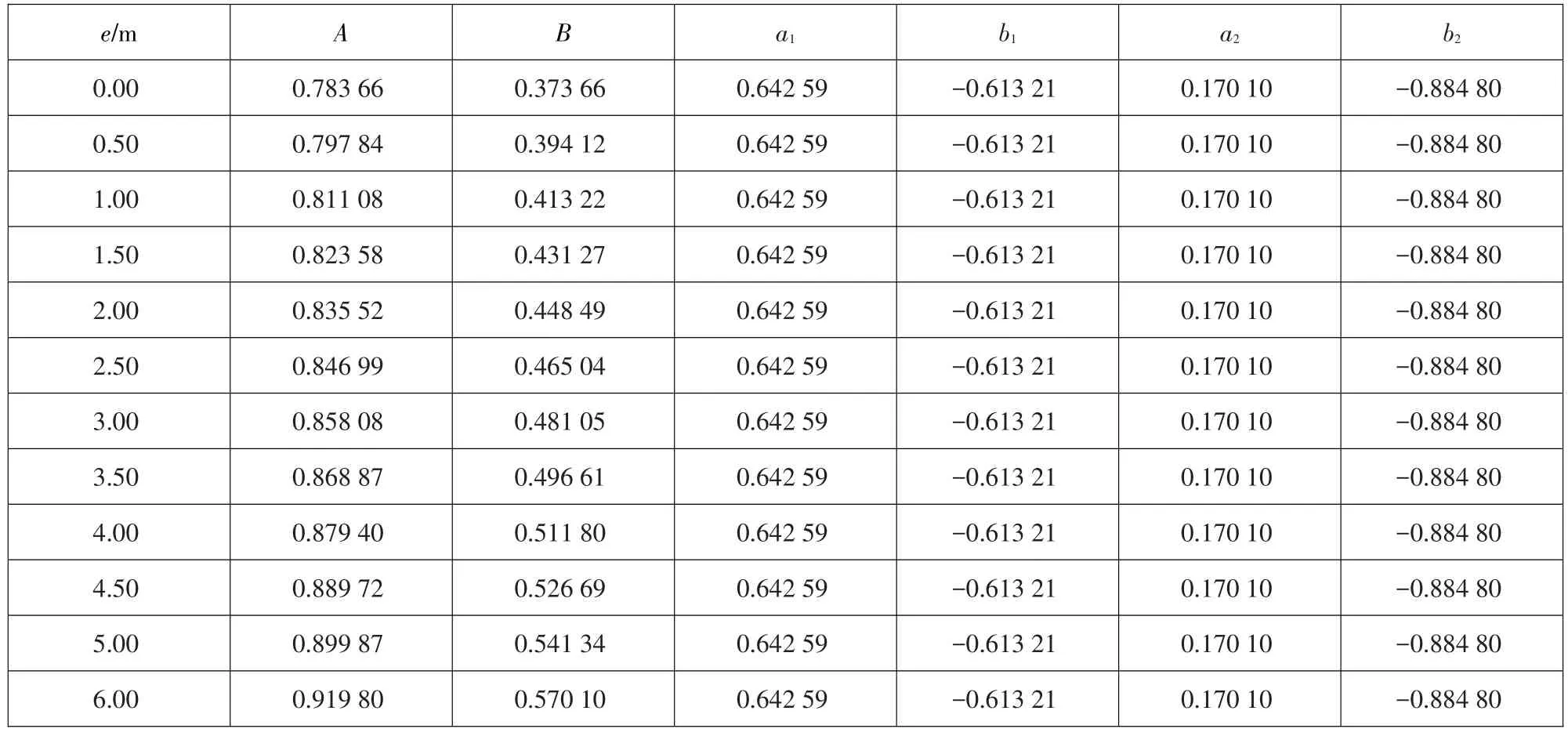
表5 不同开高时流量系数的待定系数计算表Table 5 Calculated undetermined coefficients for flow coefficients with different gate opening

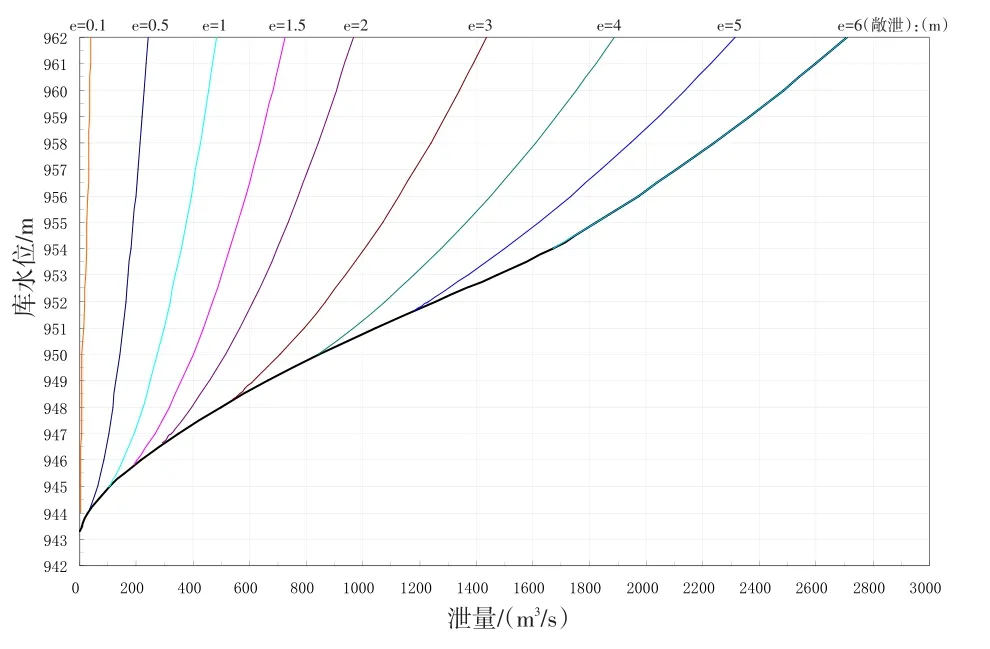
图4 闸门不同开度库水位-泄量关系曲线图Fig.4 Relation between reservoir level and flow with different gate opening

4 结论与建议

（1）在堰流时，采用优化后的综合流量系数m'=0.344 8精度较高，也可以直接应用2010年模型试验率定的流量值；

（2）在闸孔出流时，溢洪道设计规范推荐的公式虽然能够满足精度要求，但仅仅在敞泄时适用。手册中虽然有弧形闸局开流量公式，但是误差较大，采用优化后的流量系数公式（9）后，能够较好地减小使用手册推荐流量系数公式带来的误差，但其精度需模型试验或原型观测进一步验证；

（3）堰流与孔流界限的确定，应以规范中宽顶堰流时的相对开度e/H=0.65作为初步计算设计时的参考，而以模型试验数据分析后的界限值作为优化后公式的界限。必要时在模型试验中加密数据，增加一个过渡段另行计算流量系数，那么精度会进一步得到提高；

（4）为了水库防洪安全与正常运用，水闸局开时的“水位-开高-泄量”关系应作为水闸水工模型试验时的必设项目；

（5）必须做好水库的原型观测，可以说原型观测是最有力度、最为精确的水工模型试验，通过其测量值可以对理论公式进行重新率定和修正。

[1]吴持恭.水力学[M].北京：高等教育出版社，2008.

[2]李炜.水力计算手册（第二版）[M].北京：中国水利水电出版社，2006.

[3]DL/T5166-2002，溢洪道设计规范[S].北京：中国电力出版社，2002.

[4]SL265-2001，水闸设计规范[S].北京：中国水利水电出版社，2001.

[5]王挺力，侯振伦，王晖.册田水库溢洪道水力特性物理模型试验[J].科学之友，2012.（1）:59-61.