岩心三维图像修复算法

岳桂华，滕奇志，何小海，陈冬冬

（四川大学电子信息学院，610065，成都）

在石油地质分析过程中，通常需要获得三维岩心结构来定量地研究渗流的微观机理，但在实际工作中，有很多种因素造成岩心的缺失或缺损，导致很难获得完整的可供分析的岩心三维图像。如CT（computed tomography）机在岩石三维成像的应用中，其分辨率和样本尺寸是相矛盾的，为了得到高分辨率的孔隙结构图像，扫描的样本尺寸受到很大限制，使岩样的代表性有所欠缺。针对这一问题，目前的主要解决方案是以二维薄片为基础的三维重建［1-3］，得到具有与薄片特性相近的三维图像。但是，该方法是基于图像局部特性的数学建模，重建结果与真实岩心的形态结构存在一定差异，且对于多相、非均质以及原始灰度的岩心三维图像的重建存在较大的困难。将大尺寸样本切割为多个小样本，用CT分别对小样本进行扫描，再将获取的小样本的高分辨率图像拼接成较大的三维图像，能有效地解决这一问题。然而，由于物理切割导致三维图像存在较大范围的信息缺失，在小样本图像拼接成大样本图像的过程中需要恢复缺损的信息。因此，可考虑采用图像修复的方法修复出缺损的信息，从而保持原始岩心三维图像的结构和细节特征。

图像修复［4］目前多针对二维图像，对于三维图像修复的研究还较少，且主要是针对医学图像小范围信息缺失的三维图像修复以及视频的修复。目前应用较多的就是基于偏微分方程的图像修复算法和基于样例的图像修复算法。基于偏微分方程的三维图像修复算法［5］只适合小范围缺失且细节信息较少的三维图像修复，对于较大范围缺失图像的修复会存在明显的模糊现象，且不能修复图像的纹理，因此不适合大范围缺失的岩心三维图像修复。基于样例的图像修复算法［6-10］对于存在较大范围缺失的二维图像和视频图像取得了很好的效果，其中的Criminisi算法［6-7］及其改进算法通过计算边界点的优先级值来决定填充的顺序，能够有效地修复较大范围缺失的图像。目前的基于样例的图像修复算法较多地应用在视频修复中，然而视频中每一帧都是具有完整结构和细节的二维图像，算法主要是逐帧进行，修复过程是针对二维结构和纹理的修复［9-10］。岩心三维图像的三维空间结构与视频序列图像存在本质的区别，因而不能采用传统的针对视频的基于样例的图像修复方法来修复岩心三维图像。

本文针对存在较大范围信息缺失的岩心三维图像，提出了一种基于样例的三维图像修复算法，采用三维空间结构的模板同时填补三维图像缺失部分的结构和细节，通过计算边界体素相应模板的优先级值来决定填充的顺序。同时，通过空间中的等照度面对优先级值的影响，优先合成与传播图像的结构，实现三维图像结构的连接，且避免了对于等照度线方向的讨论。针对Criminisi算法中采用全局搜索方法计算量大的问题，本文使用匹配中心因子和最大距离来限制匹配块搜索范围，结合了局部搜索和全局搜索的优点，大大减少了计算量。该算法不仅保持了原始岩心三维图像的结构和细节形态特征，而且保持了岩心的微观统计特性［11］。

1 岩心三维图像修复算法

本文提出的岩心三维图像修复算法的基本思想是：从待修复区域（目标部分）Ω的边界δΩ上选取边界体素p（p∈δΩ），以p为中心，设定固定大小的立方体模板Ψp，在p的匹配中心因子和最大距离限定的搜索范围内搜索其最优匹配块Ψq，并用Ψq中的已知体素填充Ψp中相应位置上的未知体素。

对于原始三维图像中的每一个体素q都存在一个灰度值（当体素没有被填充时为空）和置信度C（q）。C（q）表示q的灰度值的可信度，初始化为C（q）=0，∀q∈Ω和C（q）=1，∀q∈Φ。每一个边界体素p的模板（边界模板）Ψp都有一个优先级值P（p）。本文提出的算法使用了Criminisi算法的关键思想，即由边界模板的优先级值来决定边界体素的填充顺序。文中提及的体素指三维数据场中的采样点。Ψp的最优匹配块Ψq就是与Ψp最为相似的样本块，即

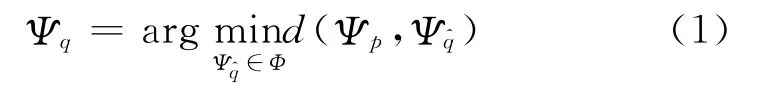
式中两图像块的距离d（Ψp，Ψ^q）为边界模板Ψp与样本块Ψ^q对应位置的已知体素的灰度值之差的平方和。

1.1 填充顺序

与Criminisi算法利用等照度线的传播来引导纹理合成的过程［6-7］类似，为了向目标区域传播大尺度的结构，本文的算法根据三维图像的等照度面给边界体素设定相应的填充顺序。等照度面指三维图像中相同亮度或强度的面，等照度线指相同亮度或强度的线。边界体素的填充顺序由其相应的边界模板的优先级值大小决定，每次都搜索优先级值最大的边界模板进行填充。边界模板Ψp的优先级值定义为

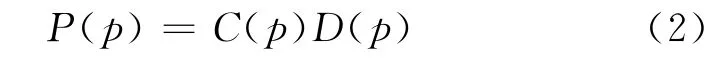
式中：D（p）为数据项，表示等照度面在边界面处的强度；C（p）为边界模板的置信度，用于衡量体素p周围模块范围内可靠信息的数量，表示为

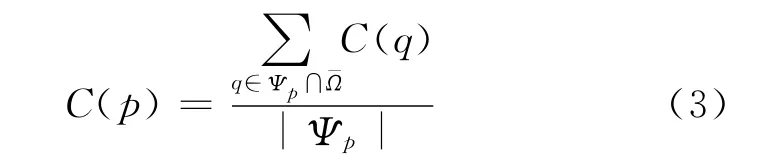
其中q∈Ψp∩表示Ψp中已被填充的体素，|Ψp|表示Ψp的体积。

在二维图像修复中，Criminisi算法取等照度线在边界垂直方向上的强度作为数据项D（p），等照度线的方向被定义为梯度方向的垂直方向。在三维图像中，等照度线的轨迹是模糊不清的，且垂直于梯度的是一个平面，存在无限多个可能的方向［12］。如图1所示，在某一小块的三维空间中存在一连续的等照度面S，取以体素q为中心的任一等照度面块ds，当区域足够小时，ds为平面或存在切面T 与梯度向量▽Ip垂直，等照度面切线方向具有不确定性，如都为ds切线，且都与▽Ip正交。在连续的边界面上，取足够小的区域得到边界平面δΩ，如图2所示，其与边界体素p所在的等照度面存在一定的夹角θ，则δΩ的法线np与梯度向量▽Ip的夹角也为θ。同时，等照度面的强度||等于梯度▽Ip的大小|▽Ip|。因此，等照度面在边界面法线方向上的强度可表示为

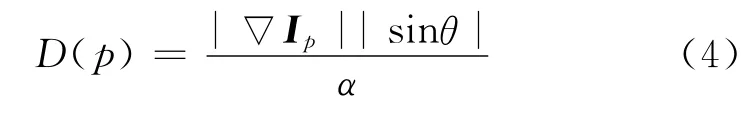
式中：α为归一化因子，取灰度等级为255，这样就避免了等照度线方向的讨论。当等照度面越强且与边界面越接近垂直状态，数据项D（p）越大，算法会优先选择这样的边界体素进行填充，即算法对结构性较强的地方会优先修复。数据项D（p）在算法中起着根本性的作用，通过D（p）实现了等照度面对填充顺序的影响，使得图像的结构（也伴随细节）优先得到合成与传播，从而将破损的结构连接起来，达到视觉上的连续性。

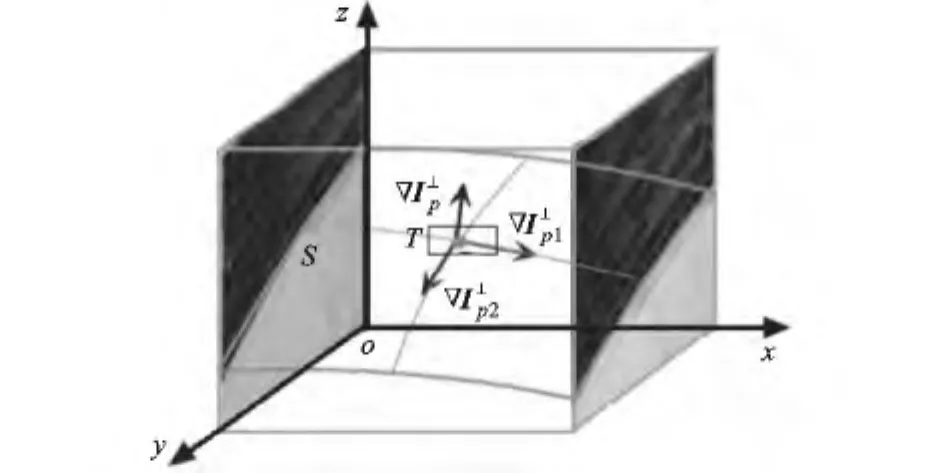
图1 三维空间中的连续等照度面

图2 D（p）的说明图

图3 匹配中心因子的原理和设置说明图

1.2 匹配中心因子和最大距离

通常图像的结构具有连续性［13］，图像的某个体素值与其周围的体素值存在一定的相关性，即图像的某个体素（或像素）的邻域具有充分的信息决定该体素值（或像素值）［8］。因此，若Ψq为边界模板Ψp的最优匹配块，p′为Ψp填充后产生的边界体素，则相应的边界模板Ψp′在Ψp周围，如图3所示，那么相应的最优匹配块Ψq′也通常在Ψq的周围，即体素q′通常在q的周围。另一方面，填充Ψp后，新的边界体素p′的边界模板Ψp′中有1／8至1的已知体素与Ψp重叠，若Ψp与Ψq完全匹配，那么Ψp′与Ψq邻近的相应位置的样本块Ψq′的匹配度为1／8至1。当修复图像的结构时，图3中的p、p′1、p″，新产生的边界模板中的所有已知体素都由刚填充的模板决定，与图中相应位置的样本块完全匹配。修复过程中，图像的结构和细节将不断地向目标区域传播，新的边界模板的信息将由周围已填充的模板决定。因此，本算法提出了采用匹配中心因子来限定匹配块的搜索范围，将匹配块搜索限定为局部搜索。匹配中心因子（MCF）是边界体素相应的匹配块局部搜索区域的中心体素。当MCF存在时，边界体素的匹配块局部搜索区域为以MCF为中心、大于或等于两倍模板大小的立方体区域。在初始化时，各边界体素的MCF为空，需全局搜索最优匹配块。当填充边界模板Ψp后，Ψp的最优匹配块Ψq的中心体素q即为新产生的边界体素p′的匹配中心因子。

匹配中心因子的原理和设置过程如图3所示。图3a中的δΩ为初始边界（白色缺损部分），算法会优先修复图像中结构性较强的地方（如p点），p的MCF初始化为空，匹配块的搜索区域为整个图像的已知区域，搜索得到的最优匹配块是以点q为中心的样本块Ψq。填充完Ψp后，如图3b所示，新的边界点p′（如p′1和p′2）的 MCF设置为q，局部搜索得到的最优匹配块为以q′（如q′1和q′2）为中心的Ψq′。对于整个图像而言，Ψq′为Ψp′的最优匹配块。匹配中心因子将匹配块搜索限定为局部搜索，大大缩小了匹配搜索范围。随着修复的进行，如图3c所示，填充Ψp′后新产生的边界体素p″的 MCF为q′1，最优匹配块为Ψq″。

最大距离表示在边界体素p的匹配中心因子不为空的情况下，局部搜索得到的最优匹配块与其边界模板的距离的最大范围，作为跳出局部搜索的条件限制。即当局部搜索得到的最优匹配块与边界模板的距离大于最大距离时，表明此处的图像结构发生了突变，该匹配块将不能作为其最优匹配块，需重新全局搜索其最优匹配块。边界体素p′的最大距离表示为

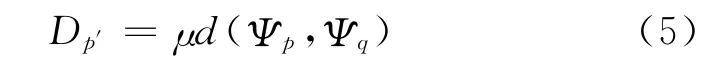
式中：μ为比例参数，通常设定为1或临近的值；p′为填充边界模板Ψp后新产生的边界体素，根据Ψp和其最优匹配块Ψq的距离，设置p′的最大距离。在设置p′的匹配中心因子的同时，设置其最大距离。该方法结合局部搜索和全局搜索的优点，大大缩小了匹配搜索范围，同时保证了匹配结果的准确性。

1.3 三维图像修复算法的主要步骤

步骤1：设定模板大小、局部搜索区域大小，并提取待修复区域Ω的初始边界δΩ0。

步骤2：计算边界轮廓上所有体素的边界模板的优先级值P（p）。

步骤3：搜索最大优先级值的边界模板Ψp。

步骤4：根据边界体素p的MCF和最大距离搜索最优匹配块Ψq，并填充相应体素的灰度值。

步骤5：更新或设置置信度、边界、新产生的边界体素的MCF和最大距离，以及边界模块的优先级值的相关信息。

步骤6：重复步骤3～5直至δΩ=∅。

选取的模板具有三维空间结构，通常为固定大小的立方体，其大小设定需有一定经验。实验中，我们将局部搜索区域设置为2倍模板大小的立方体区域。Ψp中新填充的体素的置信度设置为Ψp模板的置信度，即

当填充完边界模板Ψp后，只有Ψp周围体素的缺损情况和信息发生了变化，其余边界体素不变，因此只需搜索Ψp内及其相邻体素产生的新的边界体素，并去除已填充的边界体素，从而得到新的边界，然后计算在以p为中心、2倍模板大小的立方体邻域内的所有边界体素的模板的优先级值。整个三维图像修复算法的主要过程就是对步骤3～5的迭代，只需在算法的开始设定模板大小和局部搜索区域大小，并提取出初始边界，修复过程将会自动进行直至修复完成。

2 实验结果

首先将算法应用于存在较大范围信息缺失且结构较为简单的三维图像的修复，从而展示算法的修复过程和结果，以此验证算法的正确性。在此基础上，再对存在较大范围信息缺失的岩心三维图像进行修复。为了更加直观、准确地评估岩心三维图像的修复结果，将真实的岩心CT序列图人为地去除中间部分，模拟岩心三维图像的信息缺失，并将修复结果与真实的原始岩心CT序列图进行直观地对比观察。同时，用文献［5］中的三维图像修复算法对岩心三维图像进行了相应的修复实验，将实验结果与本文提出的算法的实验结果进行了简单、直观的对比。岩心三维图像的修复不仅要保持视觉上的连续性，达到图像修复的目的，同时要保持原始岩心的微观统计特征。由于实际应用中时常需要获取岩心三维图像的孔隙特性，且为了定量地统计分析各组实验的岩心微观统计特征，本文计算了修复结果的孔隙结构的两点能量，以及对比了修复结果与原始岩心三维图像的绝对孔隙度和有效孔隙度。

图4 结构简单的三维图像的修复过程图

2.1 结构简单的三维图像

图4为简单规则的三维图像的修复过程图，第1幅图为原始缺损图，最后1幅图为修复结果，其大小为64×64×64体素，缺失大小为20×64×64体素，设置的模板大小为7×7×7体素。由图4的修复结果可以看出，三维图像的缺失部分得到了很好地修复，保证了三维图像空间结构的连续性，视觉上几乎看不出原有的缺损，从而证明了算法对于三维图像结构修复的准确性。图4中的系列图是按照一定的时间间隔选取的，清晰地展示了算法的修复过程，可以看出等照度面强度对于填充顺序的影响，算法优先选择图像的结构进行填充，很好地传播了等照度面，有效地修复了图像的结构。同样，由于置信度的影响，在等照度面的影响相同的情况下，算法将会优先填充可靠信息较多的边界模块。

图5 岩心三维图像修复实验

2.2 岩心三维图像

我们对多组存在较大范围缺失的岩心三维图像进行了相应的修复实验，图5展示了其中1组比较典型的岩心三维图像的修复。完整的原始岩心三维图像的三维显示和各个方向的切片如图5a所示，其大小为128×128×128体素，该岩心图像噪声量较大，结构不清晰，且有一定的纹理信息，是具有一定代表性的岩心三维图像。目标部分（缺失）大小为192 704体素，其结构不规则，缺失后的图像如图5b，其中的zy切片为全白色，表示信息全部缺失的情况。图5c为本文算法得到的修复结果，使用的模板大小为9×9×9体素。图5d为采用基于PDE的三维图像修复算法所得到的修复结果，其中的迭代步长dt=0.001，迭代次数为104。由图5d可以看出，基于PDE的三维图像修复算法对大范围缺失的岩心三维图像的修复结果会存在明显的模糊现象，且不能修复图像的纹理细节，严重影响到岩心的纹理分析和渗流特性分析，直观地说明了该算法不适用于大范围缺失的岩心三维图像修复。本文的修复结果很好地填充了缺失部分，保证了三维图像空间结构的连续性，保持了原始三维图像中已知部分的结构和细节特征。

表1给出了使用本文算法进行的8组修复实验的各项统计数据，其中的有效孔隙度［14］在一定程度上表示了孔隙的连通性。两点概率函数S（r）常用于描述岩心孔隙结构的统计特征，表示三维图像中任意相隔距离为r体素的两点都为同一相的概率。两点能量［2-3］相当于修复结果和原始三维图像的两点概率函数的差的平方和，在一定程度上描述了修复结果与原始三维图像的微观统计特性的差异。图6展示了修复结果与原始三维图像在x、y、z各个方向上的两点概率函数S（r）。由表1中的两点能量和图6的两点概率函数比较可以看出，修复结果与原始岩心图像的两点概率十分相近，修复结果保持了原始完整岩心图像的统计特征，说明此三维图像修复算法对于岩心三维图像的修复是准确有效的。

表1 8组实验的各项统计数据

图6 表1中第3组实验两点概率函数

3 结 论

本文提出的三维图像修复算法能够修复较大范围缺失的岩心三维图像，修复结果保持了三维图像的空间连续性以及原始图像的结构和细节特征，修复结果与真实完整的三维图像的形态结构和统计特性都极为相似。

［1］ XU Zhi，TENG Qizhi，HE Xiaohai，et al.A reconstruction method for three-dimensional pore space using multiple point geology statistic based on statistical pattern recognition and microstructure characterization ［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2013，37（1）：97-110.

［2］ TANG Tang，TENG Qizhi，HE Xiaohai，et al.A pixel selection rule based on the number of different-phase neighbours for the simulated annealing reconstruction of sandstone microstructure［J］.Journal of Microscopy，2009，234（3）：262-268.

［3］ YEONG C L，TORQUATO S.Reconstructing random media：II Three-dimensional media from twodimensional cuts［J］.Physical Review：E，1998，58（1）：224.

［4］ 史金钢，齐春.一种双约束稀疏模型图像修复算法［J］.西安交通大学学报，2012，46（2）：6-10.

SHI Jingang，QI Chun.An image inpainting algorithm based on sparse modeling with double constraints［J］.Journal of Xi’an Jiaotong University，2012，46（2）：6-10.

［5］ MORITA S.Three dimensional image inpainting ［M］.Berlin，Germany：Springer，2006：752-761.

［6］ CRIMINISI A，PEREZ P，TOYAMA K.Object removal by exemplar-based inpainting ［C］∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway，NJ，USA：IEEE，2003：721-728

［7］ CRIMINISI A，PEREZ P，TOYAMA K.Region filling and object removal by exemplar-based image inpainting［J］.IEEE Transactions on Image Processing，2004，13（9）：1200-1212.

［8］ TANG Feng，YING Yiting，WANG Jin，et al.A novel texture synthesis based algorithm for object removal in photographs［M］.Berlin，Germany：Springer，2005：248-258.

［9］ PATWARDHAN K A，SAPIRO G，BERTALMIO M.Video inpainting under constrained camera motion［J］.IEEE Transactions on Image Processing，2007，16（2）：545-553.

［10］谷伊，韩军.基于样本的图像修补方法在视频修复中的应用 ［J］.应用科学学报，2010，28（2）：163-169.

GU Yi，HAN Jun.Video restoration using exemplarbased inpainting ［J］.Journal of Applied Sciences，2010，28（2）：163-169.

［11］TENG Qizhi，YANG Dan，XU Zhi，et al.Training image analysis for three-dimensional reconstruction of porous media ［J］.Journal of Southeast University，2012，28（4）：415-421.

［12］VAN DEN ELSEN P A，MAINTZ J B A，POL E J D，et al.Automatic registration of CT and MR brain images using correlation of geometrical features ［J］.IEEE Transactions on Medical Imaging，1995，14（2）：384-396.

［13］JARVIS R A.A perspective on range finding techniques for computer vision［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1983（2）：122-139.

［14］杨胜来，魏俊之.油层物理学 ［M］.北京：石油工业出版社，2004.