基于极限学习机的上证指数预测与分析

谭立云,刘海生,谭 龙

(1.华北科技学院基础部,北京 东燕郊 101601;2.武汉大学经济与管理学院,湖北 武汉 430072)

0 引言

证券市场是金融市场中最具魅力的市场，每位投资者都想从证券交易中获取高额利润。然而证券市场是一个典型的具有随机性、时变、波动性较大的非线性系统，难以建立精确的数学模型，多年来，人们一直在寻找有效方法试图对证券市场建立精确的预测[1]。许多学者采用传统回归分析和时间序列方法对证券市场进行了预测和分析，通过证券价格的历史时间序列挖掘其变化趋势[2-5]。然而这些传统预测方法是假设证券价格是呈线性趋势变化的，不能反映描述实际证券市场非线性特点，预测结果可靠性不高。

80年代以来，神经网络算法得到了不断发展，由于神经网络具有自组织、自学习能力，不需要考虑数学模型的内部结构，可以对非线性系统进行无限逼近和拟合，为证券市场预测和分析的深入研究开拓了新的空间[6-7]。然而神经网络自身存在难以克服缺陷，如网络结构复杂、过拟合、泛化能力不强等，预测结果与期望值之间有一定差距。极限学习机是近十年刚提出的一种单隐层前馈神经网络的学习算法，相对于传统神经网络,该方法具有训练误差小、权重范数小、训练速度快、泛化性能强的优点[8-10]，目前极限学习机已经在许多领域的中长期预测中得到广泛应用。但尚未有应用于证券指数预测的研究报道。本文利用1991年1月2日到2014年3月19日的上证综合指数历史数据作为样本，构建了基于极限学习机的神经网络模型，为证券指数预测提供新的思路和方法。最后，将这种方法的估算结果与BP网络的估算结果作对比，结果显示该算法具有估算速度快、泛化性能强，估算精度高的优势。

1 ELM极限学习机基本理论

ELM极限学习机是单隐含层前馈神经网络(SLFN)的一种改进的新算法，2004年由南洋理工大学黄广斌副教授提出。传统的神经网络学习算法(如BP算法)需要人为设置大量的网络训练参数，并且很容易产生局部最优解。极限学习机只需要设置网络的隐层节点个数，在算法执行过程中不需要调整网络的输入权值以及隐元的偏置，并且产生唯一的最优解，与传统的训练方法相比，该方法具有学习速度快、泛化性能好的优点。

该算法是源于Huang等人提出的下面的两个定理：

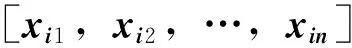
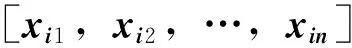
由定理1可知，若隐含层神经元的个数与训练样本个数相等，则对于任意的ωi∈Rn和bi∈R，SLFN都可以零误差逼近样本。

然而，当训练样本数较大时，为了减少计算量，隐含层神经元个数K通常要比Q小的多，定理2可知，SLFN的训练误差可以逼近一个任意的ε>0。

因此，当激活函数无限可微时，SLFN的参数并不需要全部进行调整，权值ω和阈值b在训练前可以随机选择，且在训练过程中保持不变。而隐含层与输出层间的连接权值β可以通过求解以下方程组的最小二乘解获得：

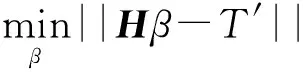
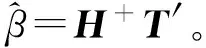
ELM在训练之前可以随机产生权值ω和阈值b，只需确定隐含层神经元个数及隐含层神经元的激活函数(无限可微)，即可计算出β。具体地，ELM学习算法主要过程分为三步：

(1) 确定隐含层神经元个数，随机设置输入权值ω及偏置；

(2) 选择一个无限可微函数作为隐含层神经元的激活函数，进而计算隐层输出矩阵H；

(3) 计算输出权值β。

2 基于Matlab的极限学习机程序实现

按照ELM的算法步骤，可以方便地利用Matlab实现ELM学习算法。

EIM训练函数elmtrain：调用格式为

[IW,B,LW,TF,TYPE]=elmtrain(P,T,N,TF,TYPE)

其中，P为训练集的输入矩阵；T为训练集的输出矩阵；N为隐含层神经元的个数(默认为训练集的样本数)；TF为隐含层神经的激活函数，TYPE为ELM的应用类型，取0(默认)表示回归拟合，取1表示分类；IW为输入层与隐含层间的连接权值；B为隐含层神经元的阈值；LW为隐含层与输出层的连接权值。

ELM预测函数elmpredict：调用格式为

Y=elmpredict(P,IW,B,LW,TF,TYPE)

Y为测试集对应的输出预测值，其它各变量含义解释同上。

3 实证分析

本文研究对象是1991年1月2日到2014年3月19日共计5677个交易日内每日的上证综合指数，指标包括开盘价、最高价、最低价、收盘价、成交量四个变量，选取每日的开盘价、最高价、最低价、收盘价、成交量作为自变量，第2日的开盘价为因变量。选取前5577个数据为训练集，后100个数据为测试集，考察极限学习机的预测效果，因为数据本身是时间序列的数据，因此所选样本均按自然时间排列，不再进行随机抽样。为了减少变量差异较大对模型性能的影响，在建立模型之前先对数据进行了归一化处理，隐含层的神经元选取20个，激活函数选取‘sig’，其他选取默认值。

限于篇幅，我们选取了测试数据的最后20个，基于极限学习机的开盘价预测值及相对误差见表1。

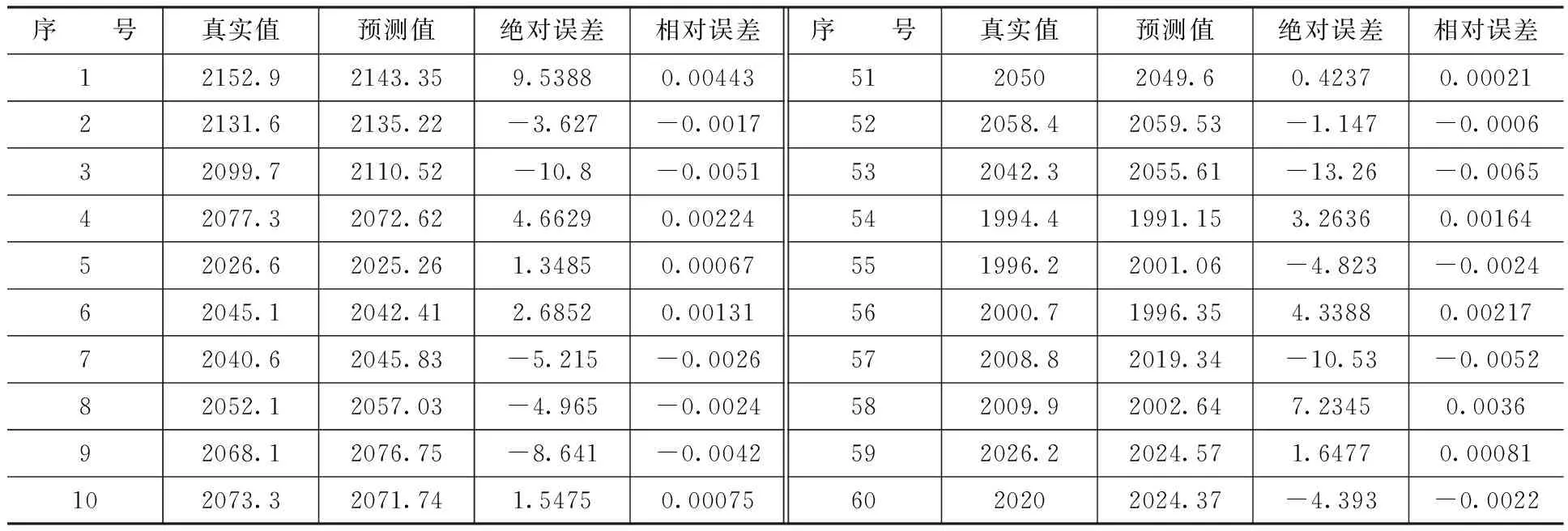
表1 ELM预测预测误差比较表

ELM预测值与真实值的对比图如1所示。

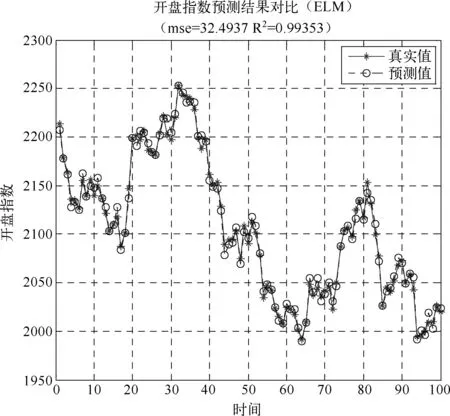
图1 上证开盘指数真实值与ELM极限学习机预测值对比图

用极限学习机网络总的均方误差MSE=32.49，复相关系数R2=0.9935。从这两个指标来讲，可见极限学习的预测精度非常高，从图形上也可以看出来预测效果非常好，精度非常高。

隐含层神经元个数对ELM性能的影响如图2所示，我们选择隐含层神经元个数20-200，计算结果显示其复相关系数都在0.992～0.994之间，没太大的区别，200之后的多个值我们也进行了计算，发现基本没变化，因此综合考虑，我们在最后的计算中隐含层神经元个数选择20个。

为了验证ELM模型的优点，本文将ELM的估算结果与BP网络的预测结果进行了对比。在同一台计算机上的MATLABR2009a中调用BP神经网络程序，隐含层取20，用Levenberg-Marquardt (LM)规则算法的BP算法对相同的样本进行训练估算，用BP神经网络预测总的均方误差MSE=581.1，复相关系数R2=0.9888，与极限学习机网络预测相比，预测效果不理想，如图3。

图2 隐含层神经元个数与复相关系数关系图

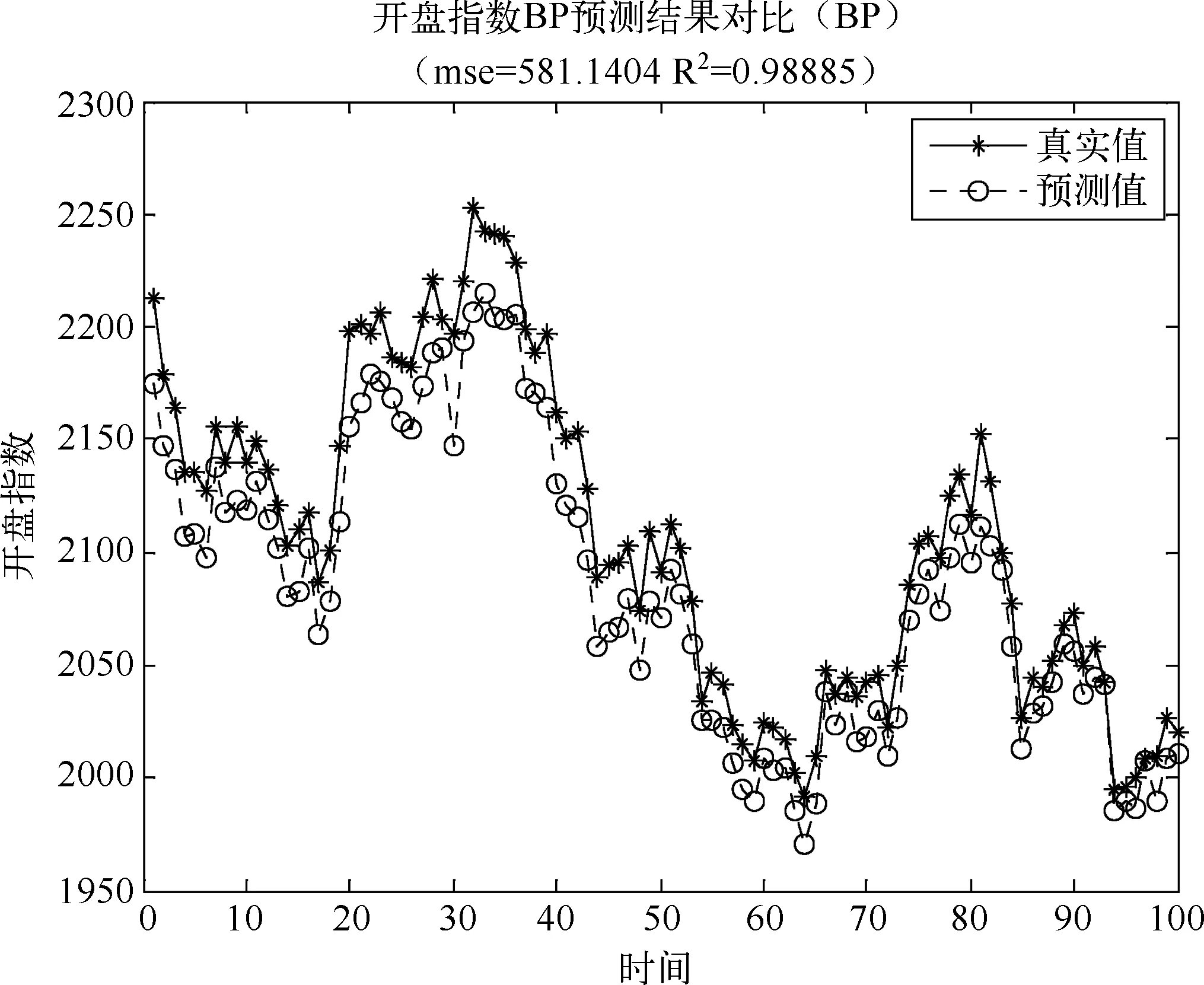
图3 BP神经网络预测对比图

4 总结

本文根据1991年1月2日到2014年3月19日上证综合指数的原始数据，建立了基于极限学习机的上证开盘指数预测模型，验证了该预测方法的可行性和有效性。通过与传统神经网络算法的比较，发现了极限学习机用于指数预测领域，预测精度和泛化能力非常令人满意，且具有简单易实现、算法稳定、估算速度快的优越性。极限学习机是一种预测精度高、误差小的证券指数预测算法，预测结果可以为用户提供有价值的参考意见。

[1] 胡杉杉，等．中国证券市场的可预测性研究[J]．财经科学，2001，(3):35-39．

[2] 周广旭． 一种新的时间序列分析算法及其在股票预测中的应用[J]．计算机应用，2005，25( 9): 2179-2184.

[3] 余敏,等．上证指数、深圳指数预测的马尔柯夫链预测模糊模型[J]．数学的实践与认识，2003，33( 9): 30-34．

[4] 马军海,等.混沌时序重构及上海股票指数预测的应用研究[J]．系统工程理论与实践，2003，12: 86-95．

[5] 谭华,等．基于模糊粗糙集挖掘方法的证券价格预测研究[J]．运筹与管理.2008,17( 4):118-124．

[6] 陈可,等．BP神经网络在证券分析预测中应用[J]．计算机工程.2001,27(11):95-97．

[7] 陈英葵．基于支持向量机的上证指数预测和分析[J]．计算机仿真.2013,30(1):297-301.

[8] 崔东文．极限学习机在湖库总磷、总氮浓度预测中的应用[J]．水资源保护真．2013,29(2):61-66.

[9] 王小川，等．Matlab神经网络43个案例分析[M]．北京:北京航空航天大学出版社,2013.

[10] 史峰,等．Matlab智能算法30个案例分析[M]．北京: 北京航空航天大学出版社,2011.