磁谐振式无线电能传输频率特性数值研究

杨东平，刘凌云，李 珊

（湖北工业大学电气与电子工程学院，湖北 武汉430068）

无线电能传输作为一种利用电磁波或电磁场进行能量传输的新技术［1］，一经提出就受到人们的广泛关注。近几年，随着科学技术的发展和生活水平的提高，尤其是伴随着MP3、智能手机、笔记本电脑等电子设备的普及，传统的有线电源供电模式已经不能满足人们对便携式设备的需求，无线电能传输引起了人们极大的研究兴趣［2－5］。无线电能传输具有能量传递便捷、无电源线困扰等特性，在小型移动设备上具有较大的应用潜力［6］。

自从特斯拉提出无线电能传输的概念［7］以后，无线电力传输一直是人们追逐的梦想，科学家们提出了许多实现无线电力传输的方法。无线电能传输主要分为3类［8］：第1类是电磁感应式，该技术相对比较成熟，传输距离近（毫米级）、效率低，电力变压器之间的能量传递就是利用此原理；第2类是电磁辐射式，主要利用微波或激光传递能量，传输距离远、传输功率大，但传输较远距离时需要高方向性天线和高效整流天线，其研制难度较大；第3类是电磁共振式，即目前主要研究的磁耦合谐振式无线电能传输技术，它采用频率在兆赫兹（MHz）范围的谐振频率，来实现电能在一个波长范围内的中等距离高效率传输，它是对感应式的突破，由美国麻省理工学院（MIT）的Marin Soljacic科研小组提出，他们也称之为 WiTricity技术［9－11］。该技术应用电磁场近场理论［12］，通过合理设计振荡器，建立了基于强磁耦合的共振能量传输系统，近区交变磁场即无线能量传输的媒介。共振是该技术实现能量传递的必要条件，可以通过设置谐振电路的谐振频率来实现。但振荡器系统的电磁性能往往与其结构单元有很大不同，因此研究振荡器系统组分之间的相互作用，对共振频率的设置具有重要意义，它影响着无线电能传输的效率。然而，迄今大多数研究都是侧重于对无线电能传输线圈参数的改进，对于组分之间相互作用对谐振频率影响的研究很少。根据近区场特性，作为发射源的天线在近距离内（米级范围）充满了不向外辐射的交变磁场，电场被大大地抑制，此时磁场强度远大于电场强度，因此可以将系统的垂直螺旋天线看作是偶极子天线。

本文从电磁学的角度出发，采用偶极子对相互作用理论，对耦合线圈之间相互作用对谐振频率影响的物理本质进行解释，并采用电磁仿真软件在兆赫兹频段对耦合线圈相互作用的物理机制进行仿真验证。仿真结果与理论分析相符，表明该理论对无线电能传输的谐振频率分析具有一定的指导意义，它相比于传统的电路分析理论更加简单易懂，为谐振频率分析开辟了一个新的思路。

1 螺旋线圈的设计

本文采用以有限元积分技术（FIT）［13］为基础的三维结构电磁场分析仿真软件。其三维模型如图1a所示。线圈的尺寸参数为：匝数N＝5、直径d＝302mm、高度h＝22mm、临近线圈圆心之间的距离p＝3mm、导线直径w＝2mm。采用的谐振单元是由漆包铜线绕制而成的螺旋线圈，电导率σ＝5.88×107S／m。衡量所选尺寸合理性的一个重要指标是品质因素Q，它与能量损耗成反比，Q值越高，能量的损耗越低，越有利于提高能量传递效率。因此对于磁共振系统，高品质因数是提高能量传输效率的关键。谐振时线圈的品质因数

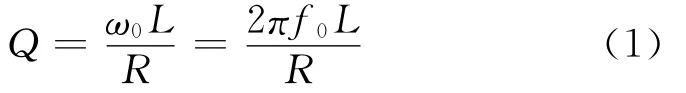
线圈参数L、R 可由下式［14－15］确定：

μ0＝4π×10－7H／m为真空磁导率。由于国际电信联盟分配给工业、科学和医学设备的自由辐射频率为13.56MHz、27.12MHz、40.68MHz、2.45GHz等，电磁辐射强度在此频率范围内不受控制［16］，因此在设计中等距离磁耦合谐振式系统模型时，应使电路的谐振频率在此范围之内（一般是1～50 MHz），此时线圈辐射电阻远小于欧姆电阻，只考虑线圈的欧姆电阻R，则

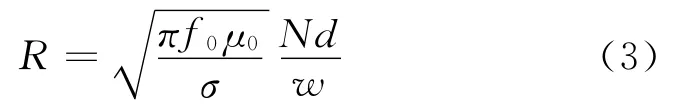
本文激励频率为10～25MHz，电磁波沿X轴方向入射，电场E沿Z轴方向，磁场H沿Y轴方向，螺旋线圈的散射参数见图1b，S11表示端口2匹配时，端口1的反射系数、S21表示端口1匹配时，端口2到端口1的反向传输系数。

图1 单螺旋线圈的仿真参数

从图1b观察到，在15.46MHz附近同时出现波谷和波峰，即谐振频率f0＝15.46MHz，线圈发生谐振是因为松散的螺旋线圈本身存在分布电容C，它与线圈电感L、欧姆电阻R构成振荡电路。将相关参数代入公式（1）（2）（3）可大概估算品质因数Q的大小为4 800左右。品质因数很高，仿真实验所选线圈尺寸大小合适。

2 螺旋线圈对之间相互作用研究

对无线功率传输模型进行数值仿真研究，线圈A、B之间的距离g＝100mm。数值仿真条件与上文一致，散射参数见图2a，从图2a可观察到：系统模型在13.51MHz附近出现波谷和波峰，系统的谐振频率（13.51MHz）小于线圈固有的谐振频率（15.46MHz），二者出现明显的偏差。由于磁耦合谐振无线电能传输技术是利用电磁场近场区的磁场传递能量，因此在近场区内，作为发射源的线圈接受到一个高频的交变电流，在近距离内（米级范围）充满了不向外辐射的交变磁场，而电场则被大大的抑制，此时磁场强度远大于电场强度，即螺旋线圈可以看做是低电压大电流的场源，可以将螺旋天线A、B看作是两个磁偶极子天线。因此用偶极子的相互作用理论可以对这一现象进行合理的解释。偶极子在入射电磁波的激励下，可以看做一个具有固有谐振频率的磁偶极子。螺旋天线对A、B在沿磁场方向上纵向排列，由图2b沿天线对轴线Hz平面上谐振时磁场的分布图可知，耦合线圈A、B的电流同相，两个磁偶极子线圈的极化方向相反，异性磁荷互相吸引，磁偶极子的回复力下降，所以图2a的谐振频率相比于图1b有所降低。

图2 双螺旋线圈的仿真实验

3 单增强线圈相互作用研究

在螺旋线圈A、B之间插入一个无源的中继线圈谐振器C，线圈A和C之间的距离是30mm，线圈C的各项参数与线圈A、B的参数保持一致。线圈C在线圈A和B能量传输过程中起到一个中转站的作用，它可以有效提高能量的传输效率。选择该模型，是由于它属于典型的交叉耦合模型，谐振频率会出现分裂现象，与前文相互对比，能更好的验证偶极子对相互作用理论在分析磁耦合谐振式共振频率方面的正确性。而对于多线圈传输机理的特性，则有待进一步的研究。数值仿真条件与前文保持一样。其散射参数如图3a所示，此时它们受到的激励磁场具有一个相位差，其谐振频率发生劈裂，出现低频（11.32MHz）和高频（15.97MHz）两个谐振点。在11.32MHz时，A、B和C天线中的电流为同相的感应电流，此时Hz平面上磁场分布如图3（b）所示，其磁场方向的变化情况与图2b一样，但图3b中磁场强度的最大值（23.7A／m）大于图2b磁场强度的最大值（18.6A／m），图3b中异性磁荷互相吸引力大于图2b，磁偶极子的回复力下降速度快，所以耦合线圈为同相电流时，图3a的谐振频率小于图2（a）。在15.97MHz时，线圈 A、C为同相电流，B的感应电流与二者相反，观察此时天线对轴线Hz平面的磁场强度分布图3c，磁偶极子线圈极化方向相同，同性磁荷互相排斥，磁偶极子的回复力增大，故谐振频率升高。综上所述，采用偶极子对的相互作用理论，能够很好地解释耦合线圈之间相互作用所引起的谐振频率变化现象，数值仿真实验与理论研究具有较好的一致性。

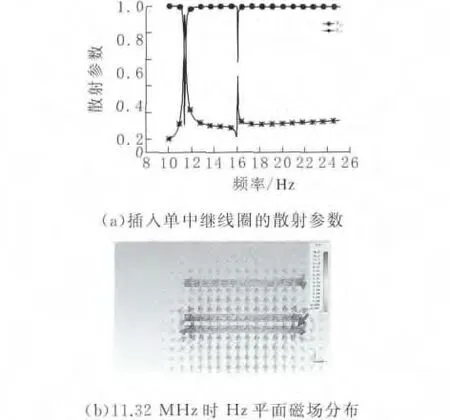
图3 插入单中继线圈的仿真实验

4 结论

本文利用数值模拟方法对基于磁耦合共振的耦合线圈相互作用机制，以及它们对谐振频率的影响进行了研究，并利用偶极子对相互作用原理对这种物理现象进行了解释，得出如下结论：当耦合线圈之间的极化方向相反时，线圈之间相互吸引，它们之间的回复力减小，谐振频率下降；当线圈的极化方向相同时，线圈之间相互排斥，它们之间的回复力增大，谐振频率升高。本研究为无线电能传输的谐振频率分析提供了新的方向。

［1］ 张茂春，王进华，石亚伟.无线电能传输技术综述［J］.重庆工商大学学报：自然科学版，2009，26（05）：485－488.

［2］ Karalis A，Joannopoulos J D，M Soljacic.Efficient wireless non－radiative mid－range energy transfer［J］.Annals of Physics，2008，323（01）：34－48.

［3］ Yuan Q，Chen Q，Li L，et al.Numerical analysis on transmission efficiency of evanescent resonant coupling wireless power transfer system ［J］.Antennas and Propagation，IEEE Transactions on，2010，58（5）：1751－1758.

［4］ Pinuela M，Yates D C，Lucyszyn S，et al.Maximizing DC－to－load efficiency for inductive power transfer［J］.Power Electronics，IEEE Transactions on，2013，28（05）：2 437－2 447.

［5］ Zhao Y，Vutipongsatorn V，Leelarasmee E.Improving the efficiency of wireless power transfer systems using metamaterials［C］／／Electrical Engineering／Electronics，Computer，Telecommunications and Information Technology（ECTI－CON），2013 10th International Conference on.IEEE，2013：1－4.

［6］ 高君宇，崔士弘，李 超.基于磁耦合共振的能量无线传输性能分析［J］.电气自动化，2013，35（03）：39－41.

［7］ Tesla N.Apparatus for transmitting electrical energy：US，1／119，732［P］.1914－12－1.

［8］ 杨庆新，陈海燕，徐桂芝，等.无接触电能传输技术的研究进展［J］.电工技术学报，2010，25（07）：6－13

［9］ Karalis Kurs A，Moffatt R，et al.Wireless power transfer via strongly coupled magnetic resonances［J］.Science，2007，317（5834）：83－86.

［10］Li Y，Yang Q X，Chen H Y，et al.Basic study on improving power of wireless power transfer via magnetic resonance coupling［J］.Advanced Materials Research，2012，459：445－449.

［11］Liu X，Zhang F，Hackworth S A，et al.Wireless power transfer system design for implanted and worn devices［C］／／Bioengineering Conference，2009IEEE 35th Annual Northeast.IEEE，2009：1－2.

［12］Bhag Singh Guru，Huseyin，Hiziroglu R.Electromagnetic field theory fundamentals［M］.周克定，张肃文，董天临，译.北京：机械工业出版社.2000.8.

［13］Weiland T.A discretization method for the solution of Maxwell’s equations for six－component fields：Electronics and Communication，（AEU），1977，31：116－120，.

［14］卡兰塔罗夫ПЛ，采伊特林ЛА，陈汤铭，等.电感计算手册［M］.北京：机械工业出版社，1992：219－227.

［15］Grandi G，Kazimierczuk M K，Massarini A，et al.Stray capacitances of single－layer solenoidair－core inductors［J］.Industry Applications，IEEE Transactions on，1999，35（05）：1 162－1 168.

［16］IEEE Std C95.1TM－2005.IEEE Standard for Safety Levels with Respect to Human Exposure to Radio Frequency electromagnetic Fields，3kHz to 300GHz.