干旱区矿区水资源综合利用和优化配置研究
连会青 ,夏向学,冉 伟 ,晏 涛
(1. 华北科技学院,北京 东燕郊 101601;2. 中国矿业大学(北京), 北京 100083)
0 引言
目前,神东矿区煤炭资源开发规模逐渐增大,矿井排水、生产、生活、工业用水量也逐年增加,出现了矿区煤炭工业及其它能源化工产业发展与区域水资源开发利用,采煤与矿区生态环境保护等诸多矛盾。因此,对神东矿区水资源现状、动态特征、变化趋势、水资源开发利用潜力及其可靠性进行评价,进而为本区水资源的合理开发,综合利用和科学管理提出科学的、具有可操作性的战略决策和技术路线,是矿区持续开发必须解决的重要课题。
1 研究区范围及可用水资源
1.1 研究区范围
研究区位于鄂尔多斯市南部的伊金霍洛旗与陕西省神木县的交界处,地理坐标约为东经110°4′到110°11′,北纬39°20′到39°30′。研究区的北部,东部,南部均为分水岭边界,西部为人为刻画的水头边界,包括大柳塔矿、活鸡兔井、上湾矿、补连塔矿、哈拉沟矿、煤液化供煤系统、石圪台矿、乌兰木伦矿。
1.2 可用水资源
研究区可用水资源主要由两大类水资源供水工程提供:自来水和复用水供水工程,其中复用水工程又包括绿化复用水和工业复用水工程。
1) 自来水供水工程
自来水供水工程主要有考考赖净水厂、哈拉沟净水厂、乌兰木伦矿地面强排孔、大柳塔井下净水工程、活鸡兔大口井、小柳塔水源供水工程和石圪台净水厂等。其中集中联网供水的水源目前有5处,即考考赖沟、公捏尔盖沟、哈拉沟、乌兰木伦矿地面强排孔(清)水和大柳塔矿井下(清)水。
到2005年底,研究区自来水供水工程现最大供水能力为37500 m3/d,枯水期供水能力为30800 m3/d。
2) 复用水工程
复用水工程包括绿化复用水和工业复用水工程。其中绿化复用水工程有大柳塔生活污水处理厂、黑炭沟生活污水处理厂、大柳塔井下水处理厂和活鸡兔井下水处理厂;工业复用水工程为各矿井即“六矿七井”井下水复用工程,主要来源于各矿井的矿井涌水。
2 规划期内需水量和供水量的预测分析
近年来,随着研究区自来水和复用水工程的扩建和增加,供水量也在增强。根据本次调查及对收集的资料分析,研究区总供水量由2005年的47293 m3/d增长到2010年的62693 m3/d,增长了15400 m3/d。
2.1 预测方法
本次水资源优化配置,采用等维灰数递补动态GM(1,1)模型建模预测2015、2020年各用户的需水量和各供水工程的可供水量。
a. 设有原始数列x(0),共有n个观察值:x(0)(1),x(0)(2),……,x(0)(n)
b. 为了减少误差,先对原始数列作平滑处理:

(k=2,3,…,n-1)
c. 对平滑处理过的数列作一次累加生成:
d. 对于数列x(1),建立预测模型的白化形式的微分方程:

式中:a,u为待估参数,a为发展灰数,u为内生控制灰数。
e. 求解GM(1,1),得到
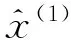
(k=1,2,……,n)
f. 下式将预测数据还原可得预测值:
(k=1,2,……,n)
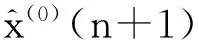
(k=1,2,……,n)
以此作为一个新的原始数列重复上述步骤1-7,直到求得最终预测结果为止。所得数据作为优化配置使用的用户需水量和供水工程可供水量。
2.2 需水量和供水量预测结果
按照上述计算方法,以2005~2010年已有的用水量数据为基础,分别对2015、2020年各用户的需水量和各供水工程的可供水量进行了预测。2015年各子区各用户需用水量是102990 m3/d,2020年各子区各用户需用水量是99290 m3/d。
3 多目标多水源多用户水资源优化配置
3.1 优化配置思路和方法
按照神东矿区规划目标,制定了模型建立准则,构建了多目标、多水源、多用户、不同水质规划模型目标函数,决策变量,目标约束以及约束条件;利用MATLAB函数fgoalattain实现了本模型的优化算法;以不同规划水平年为基准进行了水资源优化调配,提出了不同水源不同用户之间水资源综合利用调配的最优技术方案,达到了水资源供给保证率最大、用水费用最低的目的。
3.2 多目标多水源多用户水资源优化配置模型
资源多目标优化配置模型由模型、决策变量、目标函数和约束条件四部分构成。
3.2.1 数学模型
水资源多目标优化配置模型表达式为[1-6]:

其中:


V-min—极小化向量目标函数,对于极大化向量目标函数的情况,用V-max表示;

3.2.2 模型建立的准则
为实现矿区水资源的充分利用,并在保证供水满足需求的基础上,实现成本的最小化,本模型的建立原则如下:
1) 根据用户进行优先级排序,即优先满足生产的需求,其次为生活、工业、绿化。
2) 根据各水源水质的不同,各水源对不同用户供水。
3) 根据不同的用户对水质不同需求。
3.2.3 决策变量的选择
根据模型的目标把Xijk即第i个水源向第k子区第j个用户的供水量做为决策变量。
1) 把研究区划分8个子区,大柳塔、补连塔、上湾矿、煤液化供给系统、哈拉沟矿、乌兰木伦、石圪台及活鸡兔的子区标号(k)分别是1、2…8。
2) 把用户分为4种类型,即生产、生活、工业、绿化,其标号为1、2、3、4。
3) 根据水源的水质,把水源划分为三种类型,即联网自来水、工业复用水及绿化复用水编号分别是1、2、3。
所以,研究区决策变量应为8×4×3=96个。
3.2.4 目标函数的建立及目标约束
目标1:全区供水量最大限度满足各子区各用户需水要求
式中:i—用户类型编号,i= 1,2,3,4;
j—水源类型编号,j= 1,2,3;
k—子区编号,k= 1,2,3,4,5,6,7,8;
xijk—即第i个水源向第k子区第j个用户的供水量;
f1(x)—全区供水量。
目标2:全区供水量费用最小
为了克服严重的经济困难,纠正“大跃进”运动和人民公社化运动中出现的“左”倾错误,毛泽东在1961年初号召全党大兴调查研究之风。这次全党范围的调查研究,对于恢复党的实事求是的思想路线,对于制定一套具体的方针、政策和办法,对于改变“一大二公”的人民公社体制、调整农村生产关系,促进生产力的发展,起到了至关重要的作用。它是党探索社会主义建设规律的一次有益实践。
式中:i—用户类型编号,i= 1,2,3,4;
j—水源类型编号,j= 1,2,3;
k—子区编号,k= 1,2,3,4,5,6,7,8;
xijk—即第i个水源向第k子区第j个用户的供水量;
αj—第j种水源供单位水量的成本系数;
f2(x)—全区供水量费用。
3.2.5 约束条件的确定
本模型有以下四类约束:
1) 水量需求约束
水量需求约束是在满足各用户各水源需求的基础上,最大的供给量不能大于需水量的120%,以节约用水并降低用水成本。
(1) 各子区生产水量需求约束
QK生产需水≤x11k+x21k≤1.2*QK生产需水
其中:k—子区编号,k=1,2,…,8;
(2) 各子区生活水量需求约束
QK生产需水≤x12k≤1.2*QK生产需水
其中:k—子区编号,k=1,2,…,8;
(3) 各子区绿化水量需求约束
QK生产需水≤x14k+x24k+x34k≤1.2*QK生产需水
其中:k—子区编号,k=1,2,…,8;
2) 各子区各水源供水能力约束
(1) 自来水供水能力约束:
即向各子区各用户提供的自来水水量之和不能大于自来水管网和各矿自有独立水源总的供水能力。
(2) 各子区工业复用水供水能力约束:
x21k+x23k+x24k≤Qk工供
其中:k—子区编号,k=1,2,…,8;
即向各子区各用户提供的工业复用水水量之和不能大于该区工业复用水总的供水能力。
(3) 各子区绿化复用水供水能力约束:
x34k≤Qk绿供
其中:k—子区编号,k=1,2,…,8;
即向各子区各用户提供的绿化复用水水量之和不能大于该区绿化复用水总的供水能力。
3) 决策变量非负约束
xijk≥0
参与优化计算的决策变量,即各种水源向各子区各用户的供水量应该大于或等于零。
4) 决策变量零约束
根据模型建立准则及分质供水原则,①式表示绿化复用水不用于生产、生活和工业,其对应变量为零且不参与优化计算;②式表示工业复用水不用于生活,其对应变量为零且不参与优化计算。
3.3 模型求解和水资源优化配置结果
3.3.1 模型的求解
本文选择了求解多目标达到问题的matlab工具fgoalattain。为了便于在Matlab程序中实现具体算法,将96个决策变量xijk统一转化为Matlab可识别的编号形式Xm,其对应关系如下,共设置了64个变量,以大柳塔为例(表1)。

表1 决策变量xijk与程序中变量Xm的对应关系
3.3.2 水资源优化配置结果及分析
通过上述所建立的优化配置模型可得出在规划年份全区各种水源向各矿井各用户的供水情况。为更形象地反映供水情况,特分析了2015年、2020年供水网络。
从分析结果可以得出:
1) 2015年,全区总供水能力为102290 m3/d,全区需水要求96075 m3/d。根据优化解算,水资源优化配置共提供水量96075 m3/d,富余6215 m3/d,说明总供水量能够满足要求;对优化解算结果分水源进行统计,如要满足2015年需水要求,需要自来水53538 m3/d,工业复用水36390 m3/d,绿化复用水6147 m3/d;2015年全区自来水供水能力为50900 m3/d,工业复用水供水能力36390 m3/d,绿化复用水供水能力15000 m3/;工业需水共计21947 m3/d,其中包含工业复用水7094 m3/d,自来水14853 m3/d,自来水供应量占总需水量的67.7%,完全可以满足工业需水对水质的要求。
2) 2020年,全区总供水能力为99290 m3/d,全区需水要求116826 m3/d。总供水量不能够满足要求,缺口为17536 m3/d。对优化解算结果分水源进行统计,如要满足2020年需水要求,需要自来水73320 m3/d,工业复用水36390 m3/d,绿化复用水7115 m3/d;2020年全区自来水供水能力为47900 m3/d,工业复用水供水能力36390 m3/d,绿化复用水供水能力15000 m3/d;说明2020年即使工业复用水全部用完,自来水供水能力仍有不足,缺口为25420 m3/d;绿化复用水富余量很大,富余7885 m3/d。为解决自来水供水缺口,有两种方案,其一,把本区的绿化复用水富余量进行处理,提高出水水质标准,能用于工业需求,从而在工业用水中节省部分自来水,来补足自来水的用水缺口;其二提高工业复用水供水率及使用率,从而节省部分自来水出来。
4 优化配置结果对矿区供用水的指导意义
以研究区最大的用水户-大柳塔矿井为实例,具体阐明各用水户在规划年份水资源的优化配置。
大柳塔井区2015和2020年各用户水资源优化配置结果(见表2)。
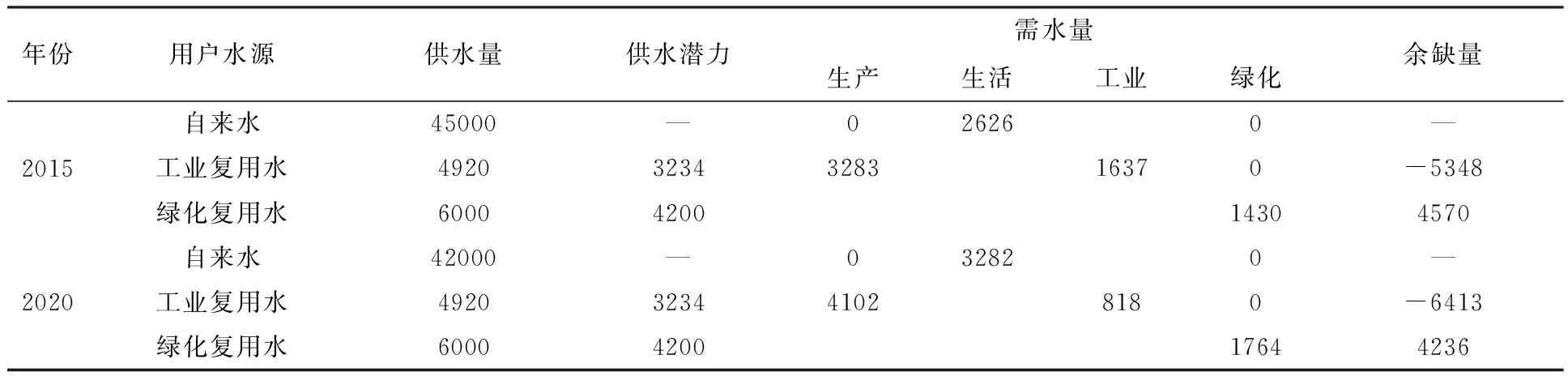
表2 大柳塔井区不同规划水平年水资源优化配置结果 m3/d
附注:自来水来自联网自来水水源;工业复用水来自大柳塔井下水直接复用和大柳塔井下水处理厂;绿化复用水来自大柳塔生活污水处理厂和大柳塔井下水处理厂;自来水供水量指面向全区的供水量。
由表中数据可以进行以下分析:
1) 供水水源及其不同水平年供水量分析
从大柳塔井区各用水来源来看:自来水来自研究区联网水源,2015年供水量为45000 m3/d,2020年供水量为42000 m3/d。工业复用水来自大柳塔井下水直接复用和大柳塔井下水处理厂, 2015和2020年供水量都为4920 m3/d。绿化复用水来自大柳塔生活污水处理厂和大柳塔井下水处理厂,2015和2020年供水量都为6000 m3/d。
2) 不同水平年水资源供需平衡分析
就工业用水而言, 2015和2020年该井区剩余的工业复用水全部用于工业用水后,还分别缺5348 m3/d和6413 m3/d。
就绿化用水而言, 2015和2020年绿化用水全部使用该井区自有的绿化复用水水源,可以满足其需水要求。
3) 水资源开发利用建议
通过上述对水资源供需平衡和供水潜力分析可以看出:就工业用水而言,单纯使用剩余工业复用水量,不能满足其需水要求。可以通过如下途径解决:一、通过提高工业复用水的供水管网能力,增加部分供水潜力,二、改进水处理工艺,提高水质标准,满足对水质要求高的工业用户。就绿化用水而言,随着未来用水量的加大,其生活污水水量也相应增加,加大对生活污水的处理力度,将为规划期绿化用水提供有力的保障。
5 结论
本文以神东矿区为例,通过水资源问题进行了深入的调查,阐述了矿区水资源多目标规划模型的理论基础,接着针对本项目规划目标及任务,制定了模型建立准则。达到了水资源供给保证率最大、用水费用最低的目的,提出了不同水源不同用户之间水资源综合利用调配的最优技术方案。按照优化配置方案,为最经济、高效的利用好现有水源,应该采取分水质、分用户分级供水的方案。在最大可能利用好现有工业复用水和绿化复用水的情况下,主要存在的问题是自来水的短缺。建议深入开展采空区及其积水水量和水质的探测和分析研究,进一步确定其分布范围、积水规模、水质状况。
[1] 张志忠, 武强, 翟德权. 徐州市岩溶水资源管理模型[J].辽宁工程技术大学学报(自然科学版), 2001, 20(6):754-760.
[2] 马振民, 武强, 付守会. 地下水资源可持续利用管理模型 研究[J]. 水利学报, 2004,(9): 1-6.
[3] 王玮, 李云峰, 侯东辉. 肥城盆地石横电厂水源地岩溶水系统地下水管理模型[J].地球科学与环境学报, 2004, 26(3): 32-38.
[4] 尹尚先,刘月琴.Application of the Boundary Element Method to Groundwater Resources Management[J]. 华南理工大学学报(自然科学版), 2002, 30(5): 86-90.
[5] 章光新, 邓伟, 何岩,等. 基于生态用水的地下水系统模拟 与优化管理模型[J]. 地理学报, 2002, 57(5): 611-618.
[6] 武强, 朱斌, 徐华.基于数字信号处理技术的地下水资源 管理模型研究—以西北某水源地规划管理模型的建立为例. 中国矿业大学学报, 2005, 34(2): 160-166.
[7] 王浩, 汪林. 水资源配置理论与方法探讨[J]. 水利规划与设计, 2004, (3): 50-56.
[8] 张发旺, 赵红梅, 宋亚新, 陈立. 神府东胜矿区采煤塌陷对水环境影响效应研究[J]. 地球学报, 2007, 28(06): 521-527.
[9] 姬亚东. 陕北煤矿区矿井水资源化及综合利用研究[J]. 地下水, 2009, 31(01): 84-90.
[10] 沈媛媛, 蒋云钟, 雷晓辉, 王明娜. 地下水数值模型在中国的应用现状及发展趋势[J]. 中国水利水电科学研究院学报, 2009, (01): 57-61.

