基于0-1序列的三相并网逆变器孤岛检测方法

王晓寰，张修北，董 杰，张纯江

（燕山大学电气工程学院，秦皇岛 066004）

引言

孤岛指主电网断网后，太阳能、风能、燃料电池等新能源并网发电系统仍向本地负载供电的现象，其分为计划孤岛和非计划孤岛［1-2］。计划孤岛指根据新能源并网的容量和故障前的运行状态、本地负荷的大小，事先确定合理的孤岛区域，在与主电网断开后，能够保证小系统的稳定运行；非计划孤岛指由于故障跳闸等偶然原因形成的孤岛。非计划孤岛发生时，由于系统供电状态不确定性和偶然性，将造成以下不利影响：可能危及电网线路维护人员和用户的生命安全；干扰主电网的正常合闸；不能控制孤岛中的电压和频率，从而损害配电设备和用户设备。由此新能源并网发电系统须安装孤岛检测装置，快速、有效地检测出孤岛状态，一旦非计划孤岛发生，立即采取相应措施，消除非计划孤岛运行可能产生的危害［3-4］。UL1741规定电网发生故障后光伏并网逆变器必须2 s内停止运行，实现孤岛保护［5］。

当微电网概念提出后，提出要充分利用孤岛效应［6］，鼓励分布式电源在主电网出现故障时，系统应该继续为用户供电，以减小停电面积，位于检测盲区内的孤岛运行条件是不应该被破坏的，否则会影响电能质量。而目前大多数的主动式检测方法对于微电网的孤岛检测都会或多或少地影响模式切换，因此，目前绝大多数的主动检测法对于微电网孤岛检测都不再适用。

经过20多年的发展，国内外基于逆变器并网的孤岛检测技术成果丰富，目前孤岛检测方法主要有被动检测法、主动检测法以及开关状态监测法3种［7］。被动式孤岛检测方法主要是检测电网的电压、频率、相位偏移以及关键电量变化率来判断有无孤岛发生［8-9］。被动式检测易于实现，对电网无干扰，不会对输出电能质量造成影响。但它在负载与逆变器输出功率匹配的时候存在较大的检测盲区，一般需和主动式检测配合使用。主动式孤岛检测方法通过对逆变器控制信号加入很小的电压、频率或相位干扰等信号，对逆变器输出进行检测［10］。当前常用的主动式方法基本思路是将电压幅值或频率等变量偏离至故障运行范围，从而判断孤岛的产生，如主动频率偏移法、滑模方式频率偏移法、带正反馈的主动频率偏移法和自动相位偏移法等［11-14］，其本质属于破坏性孤岛检测方法。为了克服传统孤岛检测方法这一缺点，本文以三相并网发电系统为研究对象提出一种新型的孤岛检测方法。该方法对并网系统的调制波进行幅值调制，实时采集并网公共点电压，提取输出电压的方差值。并网时逆变器输出电压的特征量值为零；孤岛运行时，即使在功率匹配情况下，输出电压的特征量仍是一个远远大于零的值，于是可判断孤岛发生。利用该方法检测孤岛时并网逆变器的电压和频率均在正常运行范围内，利于微电网的孤岛模式平滑转换。理论分析和实验结果证明了该方法的正确性和可行性。

1 三相并网逆变器系统

本文以三相并网逆变器为研究对象，系统带本地负载，可工作在独立和并网两种工作模式。本文的研究系统结构如图1所示，三相并网逆变器滤波器为LCL型。LCL滤波器在电压源并网逆变器中成为首选［15-16］。本地负载与输出电容并联，连接位置如图1所示。

图1 三相并网逆变器系统结构

2 基于0-1序列的孤岛检测方法

2.1 数学理论基础

方差是用来度量随机变量和其数学期望（即平均值）之间的偏离程度。方差用平方的方法消除了正负号，因而它是最常用、最重要的离散趋势统计量。标准差越大，表示变量值之间的差异越大，各数据距离均值越远。反之，标准差越小，表示变量值之间的差异越小，各数据距离均值较近。将工频周期平均分为n点（设定n=N），在每个设定时刻采集公共节点PCC点的电压（即滤波电容处电压），假设一个工频周期采样获得的电压样本分别为E （1），E（2），…，E（N）。对样本求平均值和一次方差，即样本的数字特征。计算平均值和一次方差值公式分别为

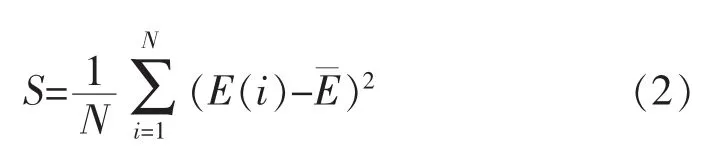
将一次方差S看成是一个随机变量，对其进行采样，继续进行样本分析，求其数字特征，经过两次求数字特征，即求取二次方差得

2.2 基于0-1序列的孤岛检测方法

本文所提出的方法属于主动式孤岛检测方法，其核心思想是对并网逆变器发电系统引入扰动，使并网逆变器输出电压发生变化，根据此变化判断孤岛，在进行孤岛判断的过程中为了不对并网发电系统的稳定性造成破坏，引入的扰动要尽量小，最好还要有一定的规律性，参考对并网逆变器发电系统引入M序列调制判断孤岛的方法，引入0-1序列，检测孤岛。M序列属于伪随机序列（伪噪声序列）的一种，是最长线性反馈移存器序列的简称，它是由带线性反馈的移存器产生的周期最长的一种序列，具有与随机序列同样的特性。0-1序列是M序列的一种特殊形式，主要有0、1两个元素，按照1001的顺序排列。0-1序列不仅具有M序列的所有优点，还克服了M序列的缺点：包含元素少，调制比较简单，操作性极强等。使用0-1序列对调制波进行调制的流程如图2所示。

在本文中取0-1序列周期为0.04 s，频率为25 Hz，利用0-1序列对调制波进行调制的具体步骤如下：

（1）将0-1序列的0，1这两个元素按 1001的顺序保存起来，并定义查询方式；

（2）调制波过零时查询0-1序列，元素为0，则将当前调制波的调制深度乘以0.99；元素为1，则将当前调制波的调制深度乘以1.01。假设三相并网系统a、b、c三相电流调制波表达式为

其中u、v、w分别代表各相0-1序列对应的当前值。每一相调制波均在过零点处调整调制深度，并维持到下一个调制波过零时刻。

调制波深度变化流程如图2所示。

图2 基于0－1序列的调制波深度变化流程

2.2.1 并网运行模式特征量计算

为具体研究孤岛产生前后特征值即二次方差值的变化，以任一相公共节点电压为例，假设PCC电压为

在理想并网工作模式下，VPCC受电网电压箝制，即使调制波幅值受到0-1序列的调制，节点电压不变。因此，并网模式的电压平均值和一次方差计算结果分别为

根据式（3）和式（4）计算二次方差值为0，即

2.2.2 孤岛运行模式特征量计算

当大电网出现断网故障，孤岛产生，此时VPCC将受到调制波调制的影响，输出电压为电流与负载的乘积，在负载固定的情况下，电压值与电流调制波有相同的幅值变化关系。为方便分析，假设从正向过零处开始调制 （系统随机检测过零点开始调制，调制起始点不同不影响分析得到的结论），其输出电压波形如图3所示。假设系统输入输出功率匹配，每一相 VPCC为公式（13）所示

图3 经过调制的输出波形

本文中设定0-1序列为100110011001…，因此实际0-1序列的周期是4π。假设以任意4π为周期计算VPCC平均值和一次方差，最终求得光伏并网逆变器公共节点电压VPCC在4π周期内的二次方差值为

根据式（12）和式（14）的计算结果，基于0-1 序列调制后的，并网系统在孤岛产生前后二次方差的变化较大。数据对比发现，当孤岛产生时，二次方差值会发生比较明显的变化，此值与VPCC的电压幅值和调制深度变化值Δ有关。

由原理分析还可以得出这样的结论：本文采用的方法是一个平均值的计算，可以有效地防止电网电压闪变时出现的伪孤岛现象。根据二次方差的变化判断孤岛，本文中选取每隔6.45×10-4s抽样一次，经过31次抽样正好是一个工频周期，这样抽得的随机样本也会具有一定的周期性，分布规律会更加明显，系统孤岛检测流程如图4所示。

本文提出一种基于0-1序列的孤岛检测方法，对电流调制波进行0-1序列调制，孤岛判定时PCC点的电压扰动在正常幅值的±1%，远远低于国际标准中设定电压正常范围的88%～110%。因此基于0-1序列的孤岛检测方法虽然通过扰动幅值来实现，但是在检测出孤岛前后均未使PCC点电压超出正常范围，属于非破坏性孤岛检测方法。

图4 孤岛检测方法流程

2.2.3 孤岛检测参数设计

基于0-1序列的孤岛检测方法属于主动式孤岛检测方法，系统参数Δ取值过大必然影响并网系统输出电流的质量。因此，需要对提出的这种主动孤岛检测方法进行谐波分析并确定Δ。傅里叶分解是谐波分析一种常用方法，经傅里叶分解获得并网电流表达式和计算系统THD（total harmonic distortion）表达式分别为

THD与调制波变化量Δ之间的关系如式（16）所示，Δ选取的越大，判断孤岛的阈值越大，越容易判断孤岛，但是Δ越大，对电流的畸变影响越大如表 1。 本课题中，选取 Δ=0.01，THD=0.4%，并网电流畸变远小于允许范围5%。

表1 建议方法Δ值与电流总畸变率的关系

与目前较为常用的主动式孤岛检测方法——主动移频（active frequency drift，AFD）方法对比，求得不同截断系数下AFD电流给定信号的各次谐波的幅值如表2所示［17］。在常用截断参数范围内，AFD方法对系统产生的THD值要大于本文提出的基于0-1序列数理统计的孤岛检测方法。

表2 AFD截断系数与电流总畸变率的关系

3 方法验证

为了验证本文所提孤岛检测方法的正确性，采用Matlab7.1对其进行仿真验证，仿真和实验平台均采用图1所示三相光伏并网系统。

图5所示为电网断开后，公共耦合点（PCC）的三相电压波形。从图中可以看出，电网断开后，公共耦合点电压幅值受调制波影响，按0-1序列有规律的变化，这为下面孤岛检测的数理分析提供了条件保证。

图5 公共耦合点（PCC）的三相电压波形

三相逆变系统输入输出功率不匹配时，孤岛在0.2 s产生，VPCC的二次方差在孤岛产生前后的变化如图6所示，二次方差值由0变化到6×105，图中纵坐标为二次方差值，横坐标为时间，单位为s。发电系统输出功率与负载消耗功率平衡情况是最难检测的情况，因此功率匹配作为检验孤岛检测方法有效性的标准之一。图7为系统输入输出功率匹配时，VPCC的二次方差在孤岛产生前后的变化，横纵坐标含义与图6相同。孤岛在0.5 s产生，二次方差值变化依然非常明显，由0变化到3.5×105。

图6 功率不匹配VPCC二次方差值

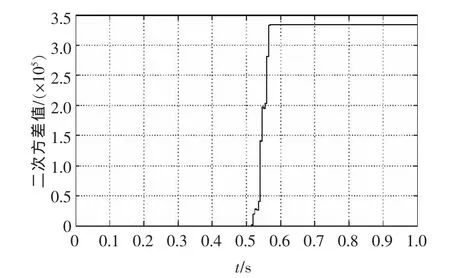
图7 功率匹配VPCC二次方差值

基于DSP TMS320F2812设计并搭建了三相光伏并网双模式逆变器实验样机。图8为从独立模式切到并网模式的二次方差波形，图9为从并网模式切到独立模式的二次方差波形。图中探头1和探头2为负载上的电压波形uLa，uLb，探头3为入网电流（ia），探头 4 为二次方差波形（F）。

图8和图9中所示逆变器工作模式进行切换，二次方差输出即产生变化，因此，根据二次方差在电网断开前后的变化即可快速地判断孤岛。

图8 独立模式切到并网模式二次方差

图9 并网模式切到独立模式二次方差

图10 为系统检测到孤岛后并网系统进行模式切换的a相负载电压实验波形。

图10 基于二次方差的孤岛检测实验波形

图10 中，ucontrol为孤岛检测后给出的模式切换指令，5 V/格，uc_a为 a 相负载电压，100 V/格。

图中t1时刻电网故障，逆变器输出电压处于电流型控制，出现明显的波动，t2时刻系统检测出孤岛，给出切换指令，系统切换到孤岛运行模式，检测时间大约为1.5个工频周期，符合国际孤岛检测允许时间要求。

4 结语

针对传统主动孤岛检测方法对电网和负载扰动大的问题，结合三相并网逆变器的特点，提出一种基于0-1序列的非破坏性主动式孤岛检测方法。该方法对系统PCC点调制波进行周期扰动并进行方差计算，根据方差值的变化判断孤岛。依据理论分析及与其他方法的对比，得出该方法具有非破坏性和对电网电流THD影响小的特点。通过仿真和实验验证了该方法适用于三相逆变器系统以及电网不平衡和输入输出功率匹配等情况，孤岛检测时间满足IEEE929—2000国际标准。

［1］Ackerman T，Anderson G，Seder L.Distributed generation：a definition［J］.Electric Power System Research，2001，57（6）：195-204.

［2］Bose B K.Energy，environment and advances in power electronics［J］.IEEE Trans on PE，2000，15（4）：688-701.

［3］王成山，肖朝霞，王守相.微网综合控制与分析［J］.电力系统自动化，2008，32（7）：98-103.

［4］Institute of Electrical and Electronics Engineers.IEEE Std 929—2000 IEEE Recommended Practice for Utility Interface of Photovoltaic （PV） Systems ［S］.New York，USA，2000.

［5］Underwriters Laboratories Inc.UL 1741 UL Standard for Safety for Inverters， Converters， and Controllers for Use in Independent Power Systems［S］.Northbrook，USA，2001.

［6］Standards Coordinating Committee 21.1547 IEEE standard for interconnecting distributed resources with electric power systems［S］.USA，2011.

［7］Yin Jun，Chang Liucheng，Diduch Chris.Recent developments in islanding detection for distributed power generation ［C］//IEEE 2004 Large Engineering Systems in Islanding Conference on Power Engineering（LESCOPE04）.Halifax，2004：124-128.

［8］Jeraputra C， Enjeti P N.Development of a robust anti-islanding algorithm for utility interconnection of distributed fuel cell powered generation［J］.IEEE Trans on PE，2004，19（5）：1163-1170.

［9］Jeong J B，Kim H J.Active anti-islanding method for Pv system using reactive power control［J］.IEEE Electronics Letters，2006，42（17）：1004-1005.

［10］Jang Sung-Ii， Kim Kwang-Ho.An islanding detection method for distributed generations using voltage unbalance and total harmonic distortion of current［J］.IEEE Trans on PE，2004，19（2）：745-752.

［11］Ropp M E，begovic M，Rohatgi A.Analysis and performance assessment of the active frequency drift method of islanding prevention［J］.IEEE Transactions on Energy Conversion，1999， 14（3）： 810-816.

［12］Hung Guo-Kiang， Chang Chih-Chang， Chen Chern-Lin.Automatic phase-shift method for islanding detection of grid-connected photovoltaic inverters ［J］.IEEE Trans on Energy Convertion，2003，18（3）：69-73.

［13］Doumbia M L， Agbossou K， Viet D T K.Correlation technique investigation for islanding detection of inverter based distributed generation［C］//IEEE Power Electronics Specialists Conference.2008：4556-4561.

［14］杨海柱，金新民.基于正反馈频率漂移的光伏并网逆变器反孤岛控制［J］.太阳能学报，2005，26（3）：409-412.

［15］Poh Chiang Loh.Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and currentsource inverters［J］.IEEE Transactions on Industry Applications，2005，41（2）：644-654.

［16］Liserre M，Blaabjerg F，Hansen S.Design and control of an LCL-filter-based three-phase active rectifier［J］.IEEE Trans on Industrial Applications，2005，41（5）：1281-1291.

［17］刘芙蓉.并网型户用光伏系统的孤岛检测技术研究［D］.武汉：华中科技大学电气工程学院，2008.