基于DSP的JPM-1型质子磁力仪研制

张 爽，周前伟，陈曙东，郭 欣，李海英

(吉林大学a.电子科学与工程学院;b.物理学院，长春130012)

0 引言

通过线圈中的直流电流产生的极化磁场将氢质子极化，利用极化后的氢质子在待测磁场中的拉莫尔进动制成的质子磁力仪是一种传统的静磁测量仪器，广泛应用于空间测磁、地质勘探和地震预测等领域［1-3］。质子磁力仪的相关研究在50～60年代国内外有大量报道［4，5］，目前已经有众多商业化产品，比如加拿大GEM公司的GSM-19T、美国的G856、北京地质仪器厂的CZM系列等。传统质子磁力仪虽然原理简单，易于实现，但要想在绝对精度、灵敏度、梯度容限、动态范围和工作温度等综合指标上达到先进水平却并非易事，需要不断地完善。

近些年，国内针对质子磁力仪的设计虽有相关报道，但很少给出详实的实验结果，而且提供的技术指标也缺乏实验验证［6-8］。笔者对JPM-1磁力仪的基本架构进行了概述，由于灵敏度是质子磁力仪的重要指标之一，而信号幅度和仪器噪声(信噪比)是影响这一指标的重要因素，因此笔者主要针对这两个方面进行了较为详细的研究，最后通过野外实验证明JPM-1型磁力仪的灵敏度可以达到0.27 nT。由于Overhauser磁力仪与传统磁力仪相比有很多共性，因此笔者的研究结果对研制Overhauser磁力仪［9-11］有一定参考价值，同时也为质子磁力仪、Overhauser磁力仪的性能评价、改进和完善提供了有益的参考。

1 质子磁力仪的工作原理

以JPM-1型质子磁力仪为例，在极化线圈中通以0.9 A的电流，在富含氢质子的探头溶液中产生7 mT的极化磁场BP，溶液内的氢质子沿线圈轴向极化;迅速关闭极化电流，BP迅速消失，氢质子磁矩将围绕待测磁场B0进动，质子进动在接收线圈中感应出的拉莫尔旋进信号的频率与地磁场成正比，通过精确测量信号频率

即可精确测量待测磁场的磁感应强度B0。其中f为拉莫尔信号频率，γp=2.675 12×108T-1·S-1为旋磁比。将γp带入式(1)可得

其中B0的单位为nT。

2 质子磁力仪系统设计

图1是JPM-1型质子磁力仪整体结构框图。该磁力仪是以DSP(Digital Signal Processor)为核心电路实现质子旋进信号的采集和处理。

图1 JPM-1质子磁力仪结构框图Fig.1 Schematic of JPM-1 proton magnetometer

极化电路由继电器和光耦等组成。极化电路为探头提供0.9 A的极化电流，并能在一个拉莫尔信号周期内撤去极化电流。在调谐电路控制上，利用优化选择配谐电容的算法实现量程范围内的自动配谐。前放电路由低噪声仪表放大器构成，放大倍数为252倍。宽带滤波、窄带滤波、低通滤波和加法电路构成信号调理电路，总放大倍数约780倍。其中窄带滤波由开关电容滤波器组成，可方便更改滤波器中心频率和增益等。A/D电路采用高精度的A/D芯片构成，高稳定的晶振提供采样频率［12］。对于频率测量，采用基于DSP的过零数频算法得到旋进信号频率，在过零点利用线性插值减小误差［13］。

为方便人机交互，仪器设置16个按键的键盘和240×64点阵液晶显示。除了完成基本测量功能外，仪器还配置了一些辅助功能，如电池电量检测、与上位机串口通信、FLASH数据存储和时钟等。

JPM-1型质子磁力仪包括探头和控制台两部分，用一根长200 cm的电缆连接。控制台为长方体铝盒(见图2)，重约4 kg;尺寸为26 cm×22 cm×11 cm。探头长170 cm，直径7 cm，重约1 kg。仪器在空闲状态，极化状态和采集数据状态时，整机电流分别为224 mA，955 mA和237 mA。电池使用铅酸蓄电池，电压为11～14 V，容量为2 A·h。

图2 JPM-1型质子磁力仪Fig.2 JPM-1 proton magnetometer

3 初始信号强度

质子磁力仪能否获得高灵敏度的关键问题是获得高信噪比的信号。JPM-1型磁力仪探头采用直筒双螺线管同轴结构，两线圈中心对称，反向绕制。这种探头结构设计使探头输出的信号为差分信号，噪声为共模信号，利于减小外界噪声。设外场方向垂直于线圈轴向，极化时间足够长，则螺线管线圈感应到的质子旋进信号初始信号强度［4，5］

其中χ为溶液的磁化率，水在温度25℃时，χ=4.015×10-9;μ0为真空磁导率;ω0为质子旋进信号角频率;n为线圈匝数;Ip为极化电流;b为线圈长度;Vi为有效溶液样品体积;η为填充因子，估算公式如下［4］

其中a为螺线管线圈平均半径rm和线圈长度b的比值。

溶液样品截面积为A，半径为ra，则

双螺线管线圈输出的初始信号幅值

由探头输出的信号，经调谐电路和信号调理电路放大后，最终被AD电路采样。AD采集到信号幅值

其中Q为调谐电路放大倍数;G为信号调理电路增益。在探头固定，极化时间足够的情况下，初始信号强度只与极化电流Ip及溶液有关。

在长春地磁场54 000 nT，利用水溶液，将参数rm=33.56 mm、ra=21.50 mm、b=51.15 mm、N=650匝、Ip=0.9 A、Q=27、G=18万倍代入式(4)～式(7)，得Vp=2.97 V，探头输出的初始信号幅值为0.61 μV;实测信号如图3所示，幅值为2.07 V，折合到探头输出信号幅值为0.43 μV。质子旋进信号是指数衰减的正弦信号，探头初始信号强度与探头结构、溶液种类、极化时间和极化电流强度等有关。实测结果与理论值基本吻合，误差主要源于实际模型与理论模型的差异。

4 仪器噪声

降低系统噪声是提高信噪比和灵敏度的重要手段［14-17］，探头和前放是噪声的重要来源之一。如图4所示，建立JPM-1磁力仪噪声模型，下面将通过建模计算和分析系统的噪声特性。

图1中r1、r2为线圈内阻，L1、L2为线圈电感，C1、C2为调谐电容，R1、R2为线圈匹配电阻。仪器前置放大系统噪声包括探头线圈内阻热噪声enr、匹配电阻热噪声enR、运放放大器电压噪声en和运算放大器电流噪声ei共4部分。这些噪声均通过后级放大电路被逐级放大，是仪器本底噪声的主要来源。

图3 实测JPM-1型质子磁力仪旋进信号Fig.3 Measured precession signal of JPM-1 proton magnetometer

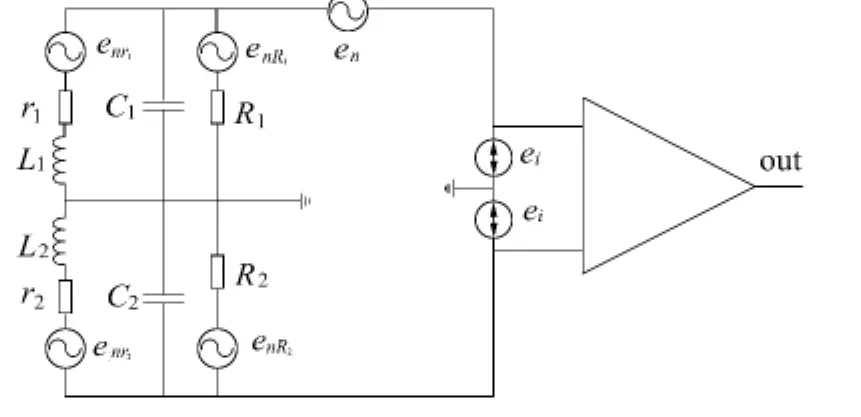
图4 探头线圈和前置放大电路噪声源等效电路Fig.4 Equivalent circuit of sensor coil and preamplifier with noise sources

前置运算放大器电压噪声由运放器件本身决定，与源阻抗无关。前置运算放大器电流噪声in，经电路源阻抗在运放输入端产生噪声电压

线圈内阻产生的热噪声折合到输入端为

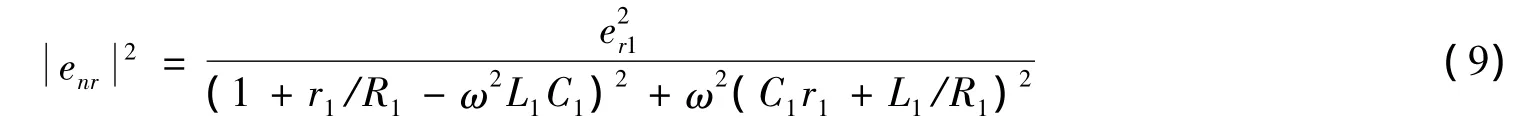
匹配电阻产生的热噪声折合到输入端为

图5 前置放大器输入端噪声理论与实测图Fig.5 Measured and predicted noise at preamplifier input

将调谐电路的谐振频率设置为2 300 Hz，调谐电容固定为 305 nF，其余参数取 r1=5.52 Ω，L1=15.86 mH，R1=20 kΩ，en=1 nV·Hz-1/2，in=2 pA·Hz-1/2，k=1.38×10-23，T=25℃;将上述参数代入式(8)～式(11)可得到如图5虚线所示仪器噪声。在谐振频率点处，电路噪声约为23 nV·Hz-1。笔者在长春野外某地进行仪器噪声测试。将采集到的噪声信号进行频谱分析，折合到输入端的结果如图5实线所示。

图5中实测噪声是经过窄带滤波后的环境噪声和仪器本底噪声之和，带外噪声因滤波使其远远小于理论值。此次实测噪声是在不加极化的条件下测量的仪器噪声，环境噪声很小，主要是仪器本底噪声，约为24.8 nV·Hz-1，与理论值基本吻合，说明构建噪声模型正确，同时说明仪器噪声是磁力仪的主要噪声。所以，优化探头设计、降低仪器噪声是提高仪器信噪比和灵敏度的重要手段。

对于质子磁力仪采集到的信号，信号信噪比RSNR的定义［15，16］为

其中σ为噪声的标准偏差。根据图3所示质子旋进信号，在信号末期(4.5 s后)旋进信号衰减为零，此时信号看作纯噪声，包括环境噪声和仪器噪声，末期信号的标准偏差为噪声强度，初始信号强度与噪声强度的比值即得到初始信号信噪比。据此计算图3信号信噪比为32∶1。

5 数频算法

国内质子磁力仪通常采用硬件数频［9］，JPM-1型质子磁力仪采用软件过零数频方法计算旋进信号频率，具体方法如图6所示。对于采样周期为Ts的旋进信号序列，质子旋进信号的过零点分别为t0，t1，…，tN，…。实际应用中设第1个过零点为起始时刻t0=0，经过nN个采样点周期，得第N个过零点tN，通过对过零点两侧的采样点线性插值可得过零点时间。tN计算方法如下

图6 基于线性插值的过零数频方法Fig.6 Signal frequency obtained using the zero-crossings of linear interpolation

由此可以计算所测信号频率

在实际中，由过零点线性插值得到的过零点的时间与过零点的真正时间存在误差［13］，误差与零点选取、信号信噪比和采样频率等有关。并且这种由线性插值误差带来的数频误差随着时间的增加而减小，但由于旋进信号信噪比也随时间不断降低，插值误差也会变大，所以存在最佳数频时间。

实验证明，基于DSP的过零数频算法实现旋进信号频率的精确测量是切实可行的，该方法相对于传统硬件数频具有节省资源、稳定可靠、易于在线更新等优点［17-20］，是现代质子磁力仪的发展方向。

6 灵敏度

灵敏度(Sensitivity)是衡量仪器是否具有重复性的重要指标。实际测试中由于环境噪声、仪器本底噪声的影响，即使探头的方向和位置不变，在同一地点的连续测量结果也不可能完全相同。灵敏度是反映仪器对同一磁场强度的大量重复读数的相对不确定性的统计值。

仪器的灵敏度在时域可用标准偏差表示，标准偏差表征的是信号的功率偏离平均值的程度。测试数据的标准偏差越小，表示仪器的稳定性越好、灵敏度越高，可通过计算大量测量结果的标准偏差评价仪器灵敏度。由于实际测量时单台仪器受日变的影响，将两台仪器测得的结果相减可以消除日变影响。故其中一台的灵敏度可用相减结果的标准偏差表示，计算公式如下

其中Δ Xi表示两台仪器第i次测量结果之差为N个测量相减结果的均值。

在长春市郊净月潭附近，将两台仪器相隔30 m左右，每隔20 s进行一次测量，共测得200点数据，测量结果如图7所示。

图7 JPM-1实验结果Fig.7 The measured result

图7a为利用两台仪器实测的结果，其中一号仪器磁场值均值为54 760.04 nT，二号仪器磁场值均值为54 757.68 nT。将两台仪器测量结果相减，消除日变后，得到如图7b的数据。根据式(15)可得JPM-1磁力仪的灵敏度为0.27 nT。

7 结语

JPM-1型质子磁力仪采用DSP为核心控制和信号处理单元，基于DSP实现了环境噪声评价和软件过零数频，野外实测结果表明，该磁力仪灵敏度可达0.27 nT。该磁力仪信号初始幅度理论值为0.62 μV，实测值为0.43 μV;该磁力仪谐振点噪声功率谱密度为24.8 nV·Hz-1/2。

基于DSP的软件测频方法与传统的硬件测频方法相比，节省硬件资源，抗干扰能力强，便于新算法软件升级;利用DSP可以快速、实时评价环境噪声和信号质量，并根据评价结果灵活更改数频时间等参数，从而提高了仪器的梯度容限，扩大了磁场测量范围。

质子磁力仪的技术指标包括:绝对精度、灵敏度、梯度容限、动态范围、测量周期、温漂、时漂和工作温度等，提高这些技术指标的研究是提高JPM-1型传统质子磁力仪综合性能的关键，也是研发JOM-1型Overhauser质子磁力仪的基础。笔者对灵敏度进行了研究，其他相关技术指标的研究目前正在开展。

［1］MARIO H ACU～NA.Space-Based Magnetometers［J］.Review of Scientific Instruments，2002，73(11):3717-3736.

［2］JAMES LENZ，ALAN S EDELSTEIN.Magnetic Sensors and their Applications［J］.Sensors Journal，2006，6(3):631-649.

［3］JOHNSTON M J S，MUELLER R J，WARE R H，et al.Precision of Geomagnetic Field Measurements in a Tectonically Active Region ［J］.J Geomag Geoelectr，1984，36:83-95.

［4］PAINI G，SYELTO O.Signal-to-Noise Consideration in a Nuclear Magnetometer［J/OL］.(1962-10-23).［2013-08-01］.http://link.springer.com/article/10.1007%2FBF02887200.

［5］吴苍生，戴光曦，刘功谆.弱磁场中质子的自由进动和一个野外测磁场的实验［J］.物理学报，1965，21(6):1175-1187.WU Cangsheng，DAI Guangxi，LIU Gongchun.An Experimental Study of Proton Free Precession in a Weak Magnetic Field and Its Application to Field Work［J］.Acta Physica Sinica，1965，21(6):1175-1187.

［6］姜惟诚，唐吉荣.分量质子旋进式磁力仪［J］.仪器仪表学报，1981，2(1):24-30.JIANG Weicheng，TANG Jirong.A Component Proton Precession Magnetometer［J］.Journal of Scientific Instrument，1981，2(1):24-30.

［7］陈忠义.质子旋进磁力仪［J］.地震研究，1982，5(4):499-516.CHEN Zhongyi.The Proton Precession Magnetometer［J］.Journal of Seismological Research，1982，5(4):499-516.

［8］赵志鹏，董浩斌.低功耗高精度质子旋进式磁力仪的设计［J］.石油仪器，2007，21(2):13-15.ZHAO Zhipeng，DONG Haobin.Design of the Low Power Consumption and High Precision Proton Magnetometer［J］.Petroleum Instruments，2007，21(2):13-15.

［9］王应吉，李伟，孙淑琴，等.基于MSP430质子旋进式磁力仪的设计［J］.吉林大学学报:信息科学版，2006，24(3):336-340.WANG Yingji，LI Wei，SUN Shuqin，et al.Design for Proton Precession Magnetometer Based on MSP430 ［J］.Joumal of Jilin University:Information Science Edition，2006，24(3):336-340.

［10］石艳林，董浩斌.Overhauser磁力仪初步设计［J］.仪表技术与传感器，2008，18(2):18-19.SHI Yanlin，DONG Haobin.Preliminary Design of Overhauser Effect Magnetometer［J］.Instrument Technique and Sensor，2008，18(2):18-19.

［11］谭超，董浩斌，葛自强.OVERHAUSER磁力仪激发接收系统设计［J］.仪器仪表学报，2010，31(8):1867-1872.TAN Chao，DONG Haobin，GE Ziqiang.Overhauser Magnetometer Excitation and Receiving System Design ［J］.Chinese Journal of Scientific Instrument，2010，31(8):1867-1872.

［12］WANG Xuying，LU Yinghua，ZHANG Likun.Design and Implementation of High-Speed Real-Time Data Acquisition System Basedon FPGA［J］.The Journal of China Universities of Posts and Telecommunications，2006，13(4):61-66.

［13］周峰，赵春宇，黄震宇.基于时域线性插值的信号周期计算方法及误差分析［J］.仪器仪表学报，2011，32(8):1724-1730.ZHOU Feng，ZHAO Chunyu，HUANG Zhenyu.Time-Domain Linear Interpolation Algorithm and Its Error Analysis for Estimating Signal Period ［J］.Chinese Journal of Scientific Instrument，2011，32(8):1724-1730.

［14］JAMES A R，KOEHLER.Proton Precession Magnetometers，Revision3［DB/OL］.(2012-05-07).［2013-08-01］.http://members.shaw.ca/jark/ProtonPrecessionMagnetometers.pdf.

［15］HANCKE G P.The Optimal Frequency Estimation of Noise Sinusoidal Signal［J］.Transactions on Instrumentation and Measurement，1990，39(6):843-846.

［16］DENISOV A Y，DENISOVA O V，SAPUNOV V A，et al.Measurement Quality Estimation of Proton-Precession Magnetometers［J］.Earth Planets Space，2006，58(1):707-710.

［17］习晓红，段清明，林君，等.核磁共振信号频率测量系统的设计与实现［J］.吉林大学学报:信息科学版，2008，26(5):448-453.XI Xiaohong，DUAN Qingming，LIN Jun，et al.Design and Realization of NMR Signal Frequency Measurement System［J］.Joumal of Jilin University:Information Science Edition，2008，26(5):448-453.

［18］宗发保，郭昌华，杜伟宁，等.基于EPM240和MSP430的等精度频率计［J］.吉林大学学报:信息科学版，2012，30(5):492-496.ZONG Fabao，GUO Changhua，DU Weining，et al.Equal Precision Frequency Meter Based on EPM240 and MSP430 ［J］.Joumal of Jilin University:Information Science Edition，2012，30(5):492-496.

［19］田宝风，段清明.核磁共振信号工频谐波的自适应滤除方法［J］.吉林大学学报:信息科学版，2009，27(3):223-228.TIAN Baofeng，DUAN Qingming.Removal Method of Industrial Frequency Harmonics in Nuclear Magnetic Resonance Signal Based on Adaptive Filter［J］.Joumal of Jilin University:Information Science Edition，2009，27(3):223-228.

［20］WANG Fei，WANG Shuxun，WU Yonggui.Frequencies Estimation of Two Dimensional Harmonics in Additive Noise with Quaternion［J］.The Journal of China Universities of Posts and Telecommunications，2005，12(3):61-66，79-85.