新型永磁磁通切换电动机的电磁性能及温度分析

王 萍，全 力，朱孝勇

(江苏大学，镇江212013)

0 引 言

长期以来，国内外学者研究较多的永磁电机大多是转子永磁型［1］，即将电枢安装在定子，永磁体置于转子。然而这种结构具有一定的局限性，同时永磁体位于转子，冷却条件差，散热困难，限制了电机的出力，制约了电机性能的进一步提高。为克服转子永磁型电机的缺点与不足，将永磁体置于定子上，即定子永磁型电机。到目前为止，关于双凸极永磁电机的本体设计、工作原理，电磁性能的分析及控制的研究成果较多［2－3］。而磁通切换电机既具备双凸极永磁电机的转子结构简单、适于高速运转等优点，又具备了转子永磁型电机空载磁链为双极性等优点，但国内外学者关于这方面的研究仍有许多的不足。

磁通切换电机具有功率密度高、转子结构简单、适合高速运行等优点［4－5］，它主要分为三大类:

一类是永磁式磁通切换电机，其气隙磁场由永磁体建立;另一类是电励磁式磁通切换电机，其空载气隙磁场通过电枢绕组产生;第三类是混合式磁通切换电机，它同时存在两个不同的磁势源，永磁体在气隙中产生一个基本不变的磁通，通过改变励磁绕组电流的方向和大小，使得气隙中磁通发生变化。

目前，对于磁通切换电机的研究成果主要为本体电磁性能分析、工作原理分析、静态特性分析、涡流损耗计算等方面。这些研究成果主要集中于对内转子式磁通切换电机的研究［4－5］，对于外转子式磁通切换电机的研究国内外鲜有报道。本文提出了以三相12/22 极外转子式定子永磁型磁通切换电机为研究目标，利用有限元软件对电机进行建模仿真，分析其电磁特性，并通过电磁－温度场耦合的方法，建立电机的稳态温度场的联合仿真，估测了电机在空载、额定运行的情况下电机各部分的温度分布情况，对电机计算所得的仿真结果和实验所测得的结果进行比较分析，验证了本文提出的新型电机模型的正确性和有效性。

1 电机的结构及工作原理

1.1 电机的基本结构

三相外转子式定子永磁型磁通切换电机结构如图1 所示。定转子皆由硅钢片叠压而成，转子为双凸极结构，位于定子外侧，转子上既无永磁体，也无绕组，永磁体嵌在定子铁心内，与空气不直接接触，绕组采用集中绕组，每4 个线圈串联成一相绕组。

图1 电机结构图

1.2 磁通切换的原理

磁通切换是指绕组里匝链的磁通(磁链)会根据转子的不同位置切换正负极性和数值大小。在一个转子极距范围内，对应着电机的一个电周期，磁通的数量会从最大变到最小，方向从进入绕组到穿出绕组。依据“磁阻最小原理”，磁通都是通过磁阻最小的路径闭合的。磁通切换电机工作原理如图2 所示［6］，图2(a)为永磁磁通沿着图示箭头的路径从定子齿进入与之相对齐的转子极，图2(b)中永磁磁通不变，但对绕组而言，路径完全相反，为穿出转子极而进入定子齿。当转子在上述两种位置之间不断运动时，绕组中匝链的永磁磁通在正负最大值之间不断变化，实现了所谓的磁通切换。

图2 磁通切换原理

2 电机的电磁分析

2.1 磁场分布

由于电机实际运行时，电机中同时存在永磁体和电枢电流，其共同作用产生了气隙磁场，故分析永磁体和电枢电流单独作用时产生的磁场。图3(a)为永磁体单独作用时产生的磁场分布，图3(b)为0°转子位置角只给A 相绕组通入直流电时磁场的分布。由图3(a)可以看出，永磁体在内部气隙有一定的漏磁。因为永磁体为切向交替充磁，电机具有聚磁效应，两块永磁体产生的磁通聚集在一起穿过气隙进入转子，这是该电机的气隙磁密远远高于其他类型永磁电机的原因。由图3(b)可以看出，该位置时电枢磁通大部分进入定转子铁心，穿过永磁体的磁力线很少。

图3 磁场分布

图4 为永磁磁场在气隙上的分布波形，图5 为电枢电流为额定电流10 A 及30 A 时的气隙磁密分布波形。永磁磁密峰值接近1.7 T，电枢电流10 A及30 A 时，电枢磁密峰值分别为0.4 T 和1.5 T，可见即使电枢电流达到额定电流的3 倍时，其产生的电枢反应磁场仍不能和永磁磁场相比。

图4 永磁气隙磁密分布

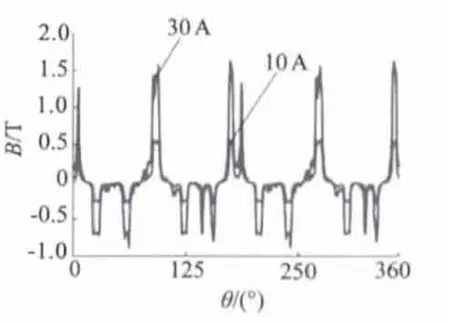
图5 电枢反应磁密分布

2.2 电机空载特性

电机在额定转速750 r/min 下运行，电机的空载特性如下。由图6 的电机空载磁链波形可以看出，电机的磁链为双极性正弦分布，与一般的双凸极永磁电机的单极性分布不同。图7 为电机空载反电动势，图8 为电机空载反电势谐波分析，从中可以看出，电机的反电动势接近于正弦波，对其进行谐波分析，电机的谐波畸变率为4.96%，除了一次谐波较大，其余的高次谐波较小，基本可以忽略不计，说明电机的反电势正弦度很高。图9 为电机的定位力矩波形，电机定位力矩很小，电机脉动很小，运行可靠。

图6 空载磁链波形

图7 电机空载反电动势

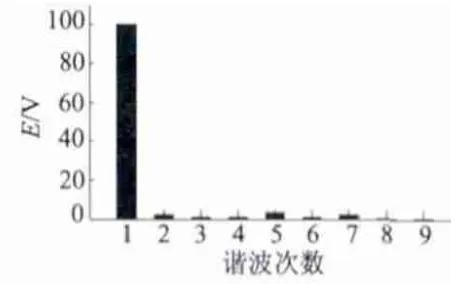
图8 反电势谐波分析

图9 定位力矩波形

3 电机的温度分析

在电机运行过程中，电机各部分的温度对电机运行时的可靠性和电机本身的寿命起着决定性的影响。故在电机设计的初始的阶段，对电机本体的温度分布进行分析是十分必要的。对传统的电机温度场分析，一般采用热路法或者是热网络法，通过假设和简化，最后形成经验公式，其计算所得到的结果一般认为是整个电机的平均温度，计算结果并不能很好地体现出电机本体各部分的温度情况。与此同时，在实际的电机运行情况下，电机的整个运行情况相当复杂，其内部各部分温度分布也各不相同。对于一个复杂的运行情况下的电机，对其进行电磁场和温度场的多物理场耦合分析是十分重要的。本文首先在Maxwell 中对电机进行建模仿真，得出相应的损耗，再利用ANSYS Workbench 与Maxwell 联合，进行电机的稳态温度场的联合仿真，仿真结果可以得出电机的每个部位的基本温度的分布云图，对计算所得出的仿真结果和实验所得出的结果进行比较分析，进一步验证本文所提出的电机模型的正确性和有效性。

3.1 温度场计算方法

为简化电机温度的计算，对电机模型进行一定的假设:假定电机沿轴向方向是连续分布的，且电机轴向温度的梯度为零。对电机进行有限元分析，将热力学的第一定律应用到一个微元体上，二维温度场的热平衡微分方程表达式［7］:

对于稳态热传递而言，温度分布对于时间的变化率为零。热平衡的微分表达式:

式(1)、式(2)中:λx，λy是材料沿x，y 两个方向的导热系数。

为求解上述方程，还需给定边界条件。常见的边界调节分为三类:

(1)温度边界条件:

(2)热流边界条件:

(3)对流换热边界条件:

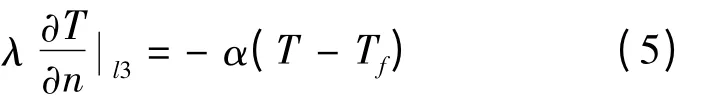
式(3)～式(5)中:T0是边界温度;q0是热源;Tf与α分别代表周围介质的温度和边界的散热系数。

3.2 电机各部件的导热系数、热生率及散热系数

求解时，将电机各部分均视为均质发热体，忽略轴向传热，即电机轴向各截面的温度相等，材料各向同性。永磁体的导热系数为15 W/(m·K)，硅钢片的导热系数为40 W/(m·K)，导线导热系数为380 W/(m·K)。

电机在运行过程中会产生损耗，这些损耗大部分转换成热量，与周围环境进行换热，最后达到温度的稳态平衡。电机的损耗可以分为铜耗、铁耗、机械损耗以及各种附加的损耗这四大类。

绕组铜耗:

电机的铁耗pFe一般由涡流损耗pe和磁滞损耗ph组成。即:

式中:ph为磁滞损耗;pe为涡流损耗;Kh为磁滞损耗系数;f 为磁场交变的频率;Bm为气隙磁密;Ke为涡流损耗系数;Δ 为硅钢片厚度;V 为铁心的体积。

由于采用联合仿真，可以由有限元软件准确计算出电机的铁心损耗和永磁涡流损耗。由于机械损耗和各种附件损耗难以用场进行精确的计算，并且在总的损耗中所占比例相对较小，故忽略不计。

生热率的物理定义是单位时间内单位体积中内热源的生成热。

式中:W 为热损耗;V 为材料体积。

电机内部温升的分析，除了需要对电机的损耗进行精确的求解外，散热系数的确定也是非常重要的。转子切向方向的运动和定子圆周表面的阻滞影响了电机气隙的冷却。故电机气隙的散热系数可表示:

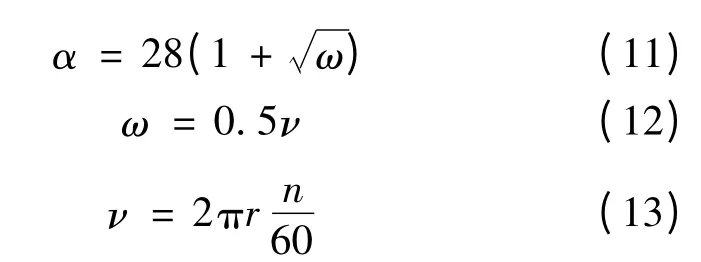
式中:ω 为气隙平均风速，v 为转子表面旋转速度。

3.3 结果和实验

由于电机属于外转子型，电机的转子与空气自然传热，散热系数较大，故电机的转子外侧温度最低。电机的转子旋转与定子间的气隙存在对流换热，故定子外侧的温度由于对流散热，温度相较于轴间温度较低。由于永磁体嵌在定子铁心上，样机定子温度分布近似于等温分布，整个定子温度差不大。图10(a)为电机空载时的温度分布，定子最高温度51°C，图10(b)为电机额定运行时的温度分布，定子最高温度为114.2°C，此时已超过永磁体的最高温度，永磁体会发生不可逆去磁。

图10 温度分布

若样机发热问题较严重，长期运行将减少使用寿命。从仿真结果可看出，电机温度最高处为定子，电枢绕组均匀分布在定子上，电机的主要损耗来自铜损。从负载时的仿真结果来看，样机的最热点温度超过了永磁体的极限温度，为了减少高温对永磁材料性能的影响，因此解决样机的发热问题尤为紧迫。一般可通过降低电机的损耗大小或者改善散热条件等多种散热方式来解决样机的发热问题。图11 为轴向强迫通风冷却电机时的温度分布，定子最高温度为73.4°C，定子轴侧温度将降低明显，最低温度为51°C。对比有限元仿真结果可以看出，对电机轴向进行通风，电机的整体温度有了明显的降低。

图11 轴向通风温度分布

为了验证仿真的合理性，在实验室中制作了1 kW 的实验样机，在相同的冷却条件下，实测温度与仿真温度的比较如表1 所示。由表1 可以看出，除了电机运行在15%的额定负载情况时，实测温度和仿真结果基本接近。电机运行在15%的额定负载情况时，仿真温度要远高于实际温度，主要是因为仿真中电机的初始温度设置比电机低负荷运行时实际的温度要高。

表1 实测温度与仿真温度相比较

4 结 语

本文介绍了一种新型的永磁磁通切换电机，详细分析其结构、工作原理及电机电磁特性，仿真和实验结果表明该电机设计的合理性。将电磁场及温度场都考虑在电机的设计过程中，采用电磁－温度场耦合仿真，得到电机的温度分布。同时利用合理的通风散热方式，改善电机的发热，比较仿真结果和实验测得的温度，其结果是基本接近的，进一步验证了本文所提出的电机模型的可行性和正确性。

［1］ CHEN Y S. Motor topologies and control strategies for permanent magnet brushless AC drives［D］.Sheffield，UK:University of Sheffield，1999.

［2］ 孙亚萍，闵莹，胡春玉.结构对永磁双凸极电机性能影响的分析［J］.微电机，2009，42(2):26－28，46.

［3］ 崔巍，龚宇.双凸极永磁电机的对称化设计［J］.浙江大学学报(工学版)，2011(5):43－48.

［4］ 许泽刚，谢少军.磁通切换电机研究现状及展望［J］.常州工学院学报，2010(21):31－36，44.

［5］ 王道涵.新型磁通切换磁阻电机系统的分析、设计与控制研究［D］.济南:山东大学，2010.

［6］ 朱孝勇，刘修福.新型磁通切换电机优化设计与动态建模仿真［J］.电机与控制应用，2012(12):5－10.

［7］ 黄丽华，吴海鹰.带阻尼条的永磁无刷直流电机转子温度场分析［J］.船电技术，2008(1):21－24.