基于高频旋转电压注入法的IPMSM 转子位置估算策略

吕睿龙，孙丽萍，杨贵杰

(1.东北林业大学，哈尔滨150040;2.哈尔滨工业大学，哈尔滨150001)

0 引 言

永磁同步电动机以其优异的性能广泛应用于机床、冶金、纺织等工业领域。永磁同步电动机控制系统多采用矢量控制策略，需要通过位置传感器确定电机转子位置，不仅增加了成本，还降低了系统可靠性。因此消除传感器可以降低成本、减小体积并提高系统可靠性，成为当今电机控制研究的热点问题［1－4］。

近年来，由于跟踪电机凸极的高频信号注入法可以应用在电机低速及零速状态下具有鲁棒性好，且对电机参数不敏感的特点，高频信号注入法获得到广泛应用［5－7］。文献［5］采用了锁相环调节转子位置误差信号，但其中包含有滤波及PI 环节，具有一定的滞后性;同时锁相环只能对输入量进行跟踪，在电机转矩突然变化时无法及时识别，只能在系统发生变化后做出反应，因此锁相环无法将及时地响应电机转矩扰动。本文将采用高频旋转电压注入法来获取转子位置信息，并采用伦伯格观测器进行转子位置的电角度估算以及转速估算。

1 高频信号注入下内嵌式永磁同步电动机模型建立

1.1 内嵌式永磁同步电动机(IPMSM)的数学模型

如图1 所示，在IPMSM 坐标系统中a，b，c 为定子的静止三相坐标系;α，β 为两相静止坐标系，定义α 轴与a 轴相重合;d，q 为以转子保持同步的同步坐标系;θe为转子参考旋转坐标系的d 轴超前于α轴的电角度;ωe为转子旋转时的电角速度。

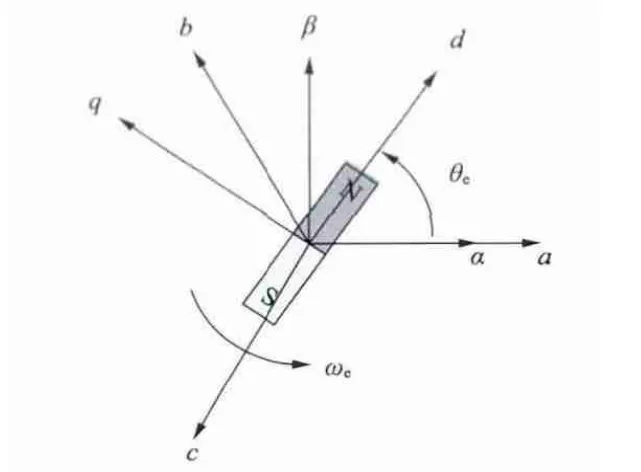
图1 IPMSM 转子静止和旋转坐标系示意图

IPMSM 在同步坐标系下的电压和磁链方程［10］:式中:ud，uq为在d，q 坐标系下的定子电压;Rs为定子电阻;id，iq分别为直轴(d 轴)电流和交轴(q 轴)电流;p 为微分算子;ψd，ψq为d，q 坐标系下的定子磁链;Ld，Lq分别为直轴电感和交轴电感;ψf为转子的永磁磁链。为了方便起见，可设If为转子永磁磁链的等效励磁电流。

IPMSM 的转矩方程:

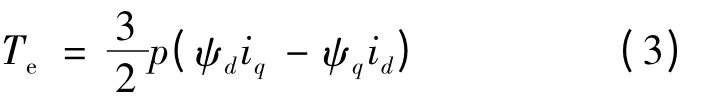
根据式(2)可得:

式中:Te为输出的电磁转矩;p 为电机极对数。由式(1)～式(4)可以看出，电磁转矩实际上包含两部分，一部分是由iq输出的电磁转矩，另一部分是因Ld，Lq不相等导致的磁阻转矩。

根据坐标变换方法，将IPMSM 旋转坐标系下的数学模型转换为静止坐标系下的数学模型:

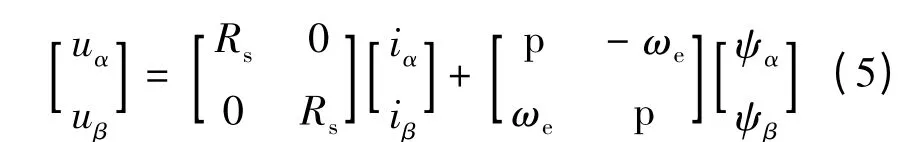
式中:uα，uβ分别为静止坐标系下的α，β 轴电压;iα，iβ为静止坐标系下的α，β 轴定子电流;ψα，ψβ为静止坐标系下α，β 轴定子磁链。

考察电感矩阵L(θe)，将其变换为静止坐标系下［26］:

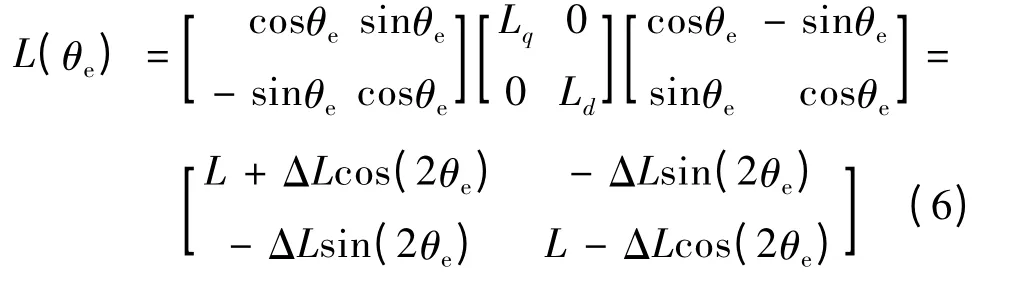
此时静止坐标系下的定子磁链方程可表示:

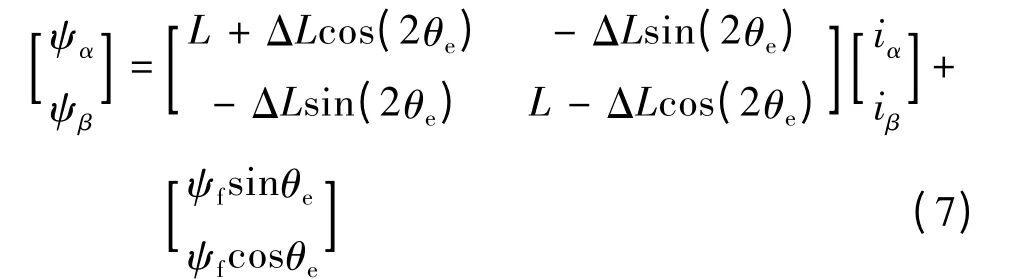
将式(7)代入式(5)中，可得:

由此可见，由于IPMSM 具有的凸极特性，导致电感L 在电机旋转时发生变化，最终反应到定子的磁链方程中，因此可以通过注入高频旋转电压的方法，通过提取定子电流中的高频响应分量解调出转子的位置信息。

1.2 高频注入下IPMSM 数学模型

静止坐标系下注入的高频电压uh:

注入高频电压的电机定子电压方程以及磁链方程分别表示［32］:

将注入的高频旋转电压式(9)代入电机的定子电压式(11)中，同时对两边求积分得出磁链方程:

将式代入式(10)中，经变换得到高频电流响应信号的数学表达式:

将高频响应电流的数学表达式由矩阵形式改写为复数形式:

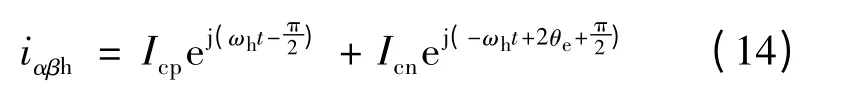
由式(14)可以看出，在正序分量中不包含转子位置信息，负序分量中包含电机转子电角度θe相关的信息，通过提取负序分量中的位置信息就可以得出转子的电角度。

图2 为注入过程的矢量形式和标量形式。注入的高频旋转电压信号可以由外部电压源提供，也可由逆变器直接提供，本文利用软件编程，将高频电压通过逆变器直接注入到电机定子中。

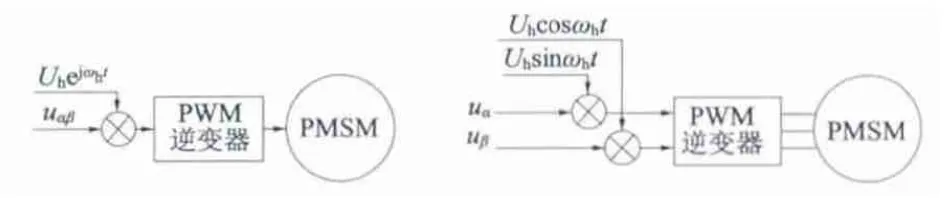
图2 高频旋转电压信号注入定子绕组示意图

将高频电压对称的注入到定子绕组中，此时高频电流在电机内部形成高频旋转的磁场［8］，由于该旋转磁场的角频率相对于电机基波角频率很大，所以高频电压不会对电机性能产生影响。电机的凸极将对注入的高频信号起到调制作用，使得最终高频电流响应信号的负序载波分量［9］携带有电机转子位置的信息，再通过对高频电流解调，最终可以估算出电机的转子位置，并以此来构成一个闭环系统，实现IPMSM 无位置传感器运行。

2 改进的IPMSM 转子位置估算策略

2.1 高频注入下电流响应信号的提取

由于定子电流基波分量和逆变器功率器件开关谐波分量的频率距离目标频率较远，而高频响应电流的正序以及负序分量频率十分接近，因此可以选择使用带通滤波器(BPF)将两者滤除，并将高频响应电流信号完全分离出来。

为了保证提取出的电流信号保持较好的特性，本文采用巴特沃斯(Butterworth)滤波器来进行滤波。因为巴特沃斯滤波器在通带范围内频率响应曲线平缓，且在阻带范围内逐渐衰减为零，同时巴特沃斯滤波器结构也较为简单［33］。因此为了保证构建的滤波器具有良好的性能，同时兼顾单片机的运算能力，本文采用四阶巴特沃斯滤波器实现通带滤波。其基本结构如下:

在通过带通滤波器滤波后，仅剩下了式(14)中的高频响应电流的正序和负序分量，其中负序分量:

相对于静止坐标系，该负序分量的旋转频率实际上是－ωh+2ωe，负序分量并不完全在中心频率上，而是随着电机的旋转发生变化。当电机高速旋转时，该频率将逐渐偏移中心频率，若超出了BPF的通带，其幅值将发生衰减，相位也将发生变化，最终影响位置估算的效果。这也可以说明在目前的情况下高频旋转电压注入法不适用于高速运行时的电机转子位置估算，而在低速运行时正序和负序分量的频率差别很小，为了提取中负序分量就需要用到同步参考坐标系滤波器SRFF(Synchronous Reference Frame Filter)。

如图3 所示，SRFF 的基本原理是将高频电流响应变换到正序分量坐在的坐标系下，此时正序分量将变为一个直流量，而负序分量者变成了近似于频率加倍的高频分量，此时再通过一个高通滤波器滤除直流分量，再将其重新变化到静止坐标系下，就可以实现负序与正序分量的解耦。

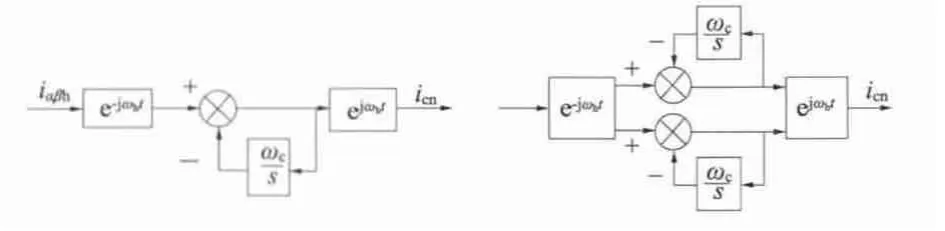
图3 同步参考系滤波器结构图

2.2 伦伯格观测器及转子位置估算

本文提出采用伦伯格观测器进行转子位置的电角度估算以及转速估算。在实际情况中电机往往呈现多凸极性，其中包括由定子设计引起的静态凸极以及由饱和产生的饱和性凸极。静态凸极是由电机转子以及定子自身设计所致，因此与电机转子的位置、定子电流的大小无关。因此通过实验即可以测出静态凸极的分布情况，并在运行过程中加以补偿。而饱和性凸极则需要加以分析。

本文采用多凸极模型解耦方法来减少饱和性凸极对转子位置估算的影响，多重凸极下的高频响应电流负序分量方程如下:

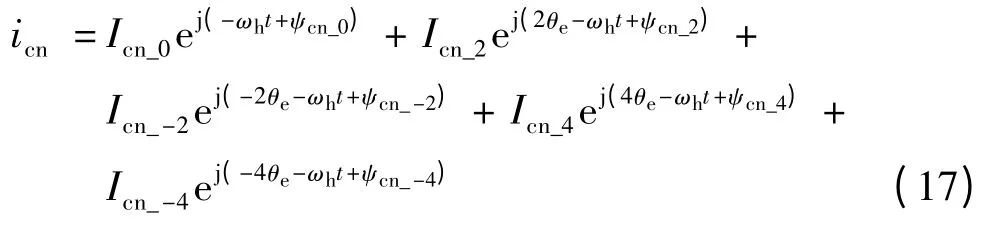
显然，负序电流的次数越高则其幅值越小，因此为了简化模型，仅考虑到k = ±2 即可。式(17)中，第一项是k=0 时电机呈现的静态凸极，由于这一负序电流与电机转子位置和磁饱和无关，其偏移值固定。因此只需要将这一负序电流变换到－ωh角速度旋转的同步坐标系下即可得到其偏移量。通过理论计算算出偏移量的值，但该方法运算复杂。实际应用中可以通过实验测出其偏移量大小，并在电机运行时通过查表法进行补偿，从而实现静态凸极的解耦，基本过程如图4 所示。

饱和性凸极的解耦与之相类似，但饱和性凸极与电机转子位置有关，在进行补偿时也需要读取转子位置信息，同时以第k 个分量的频率为中心频率构建带通滤波器，进行滤波后提取并记录不同电流值的情况下该分量的幅值以及相位，之后通过查表或曲线拟合的方式进行补偿。图5 即是在观测器中实现对式(17)的第三项进行解耦，其他次数的负序分量解耦以此类推。

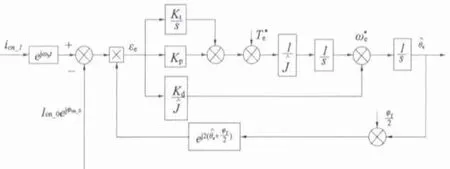
图4 带有静态凸极补偿的伦伯格观测器

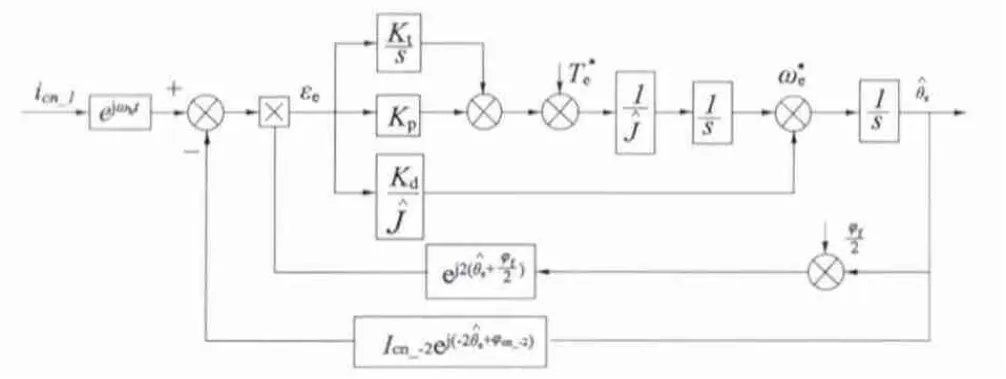
图5 带有饱和性凸极解耦的伦伯格观测器

3 实验结果及分析

以XMC4500 为核心搭建了IPMSM 实验平台，实现了基于高频旋转电压注入法对IPMSM 转子位置的估算。

实验及仿真所用电机参数如表1 所示，实验及仿真结果如图6 所示。

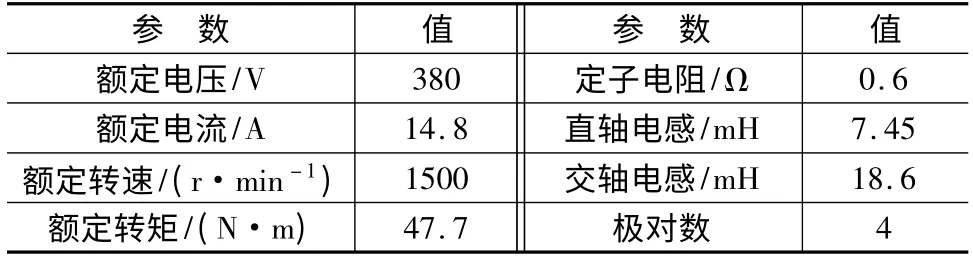
表1 实验及仿真用电机参数

图6 实验控制系统及实验平台

图7 为基于单凸极跟踪的转子位置估算仿真图形。由图7 可见，利用高频注入法和伦伯格观测器的估算方法能够准确地估算出电机转子的位置，但由于滤波器的影响，估算角度与实际角度之间有一定的相移。本文采用对误差进行补偿的方法改进观测器，可以看出此时估算位置与实际位置契合度很高。

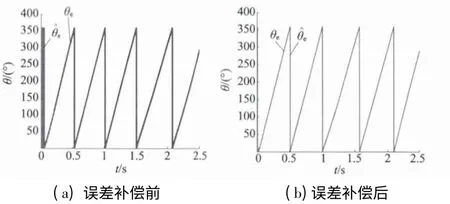
图7 补偿前后的转子位置估算对比

电机转速为50 r/min，采用伦伯格观测器的转子位置估算以及补偿后的位置估算结果如图8 所示。可以看出估算结果与实际波形之间的幅值失真度很小，误差补偿后两者已经十分接近。

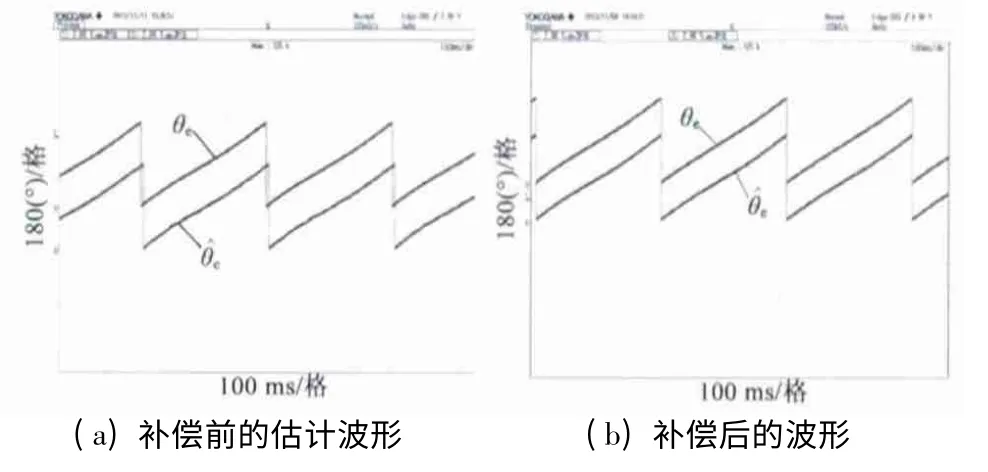
图8 相位补偿前后波形对比

图9(a)为电机转速由50 r/min 正方向变至50 r/min 负方向时的估算结果，图9(b)则是转速由50 r/min 上升至100 r/min 时的估算效果。可以看出位置估算的误差也十分稳定，正负误差不超过3°。

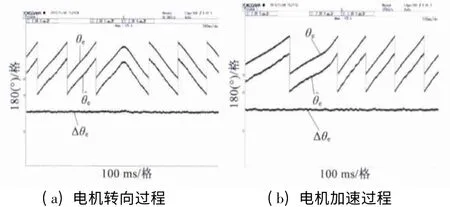
图9 转子位置估算实际值与估算值对比

4 结 语

本文分析了IPMSM 在高频旋转电压注入下的数学模型，提出了使用选取伦伯格观测器进行位置估算的方法，利用伦伯格观测器能够实现对转子位置、转速的估计，同时滤波器相位补偿以及多凸极补偿效果明显。设计并搭建了基于英飞凌XMC4500单片机的电机驱动平台，对无传感器控制系统的软件进行了编程。在此基础上进行了实验，实现了无传感器控制系统的运行。

［1］ 唐任远.现代永磁电机理论与设计［M］. 北京:机械工业出版社，1997.

［2］ 杨波. 基于高频注入法的电梯曳引机转子位置估算的研究［D］.沈阳:沈阳工业大学，2010.

［3］ 徐衍亮.电动汽车用永磁同步电动机及其驱动系统研究［D］.沈阳:沈阳工业大学，2001.

［4］ PARK M H，LEE H H.Sensorless vector control of permanent magnent synchronous motor using adaptive identification［C］//Conference of IEEE IECON Annual Meeting.1989:209－214.

［5］ 毛永乐.基于高频信号注入法的IPMSM 转自位置估算［J］.微特电机，2011，39(11):17－19.

［6］ TAKESHITA T，MATSUI N.Sensorless control and initial position estimation of salient－pole brushless DC motor［J］.Advanced Motion Control(AMC)，1966，1:18－23.

［7］ JUNG I H，IDE K，SAWA T.Sensorless rotor position estimation of an interior permanent－magnent motor from initial states［J］.IEEE Transactions on Industry Applications，2003，39(3):761－767.

［8］ 王丽梅.基于高频信号注入的永磁同步电动机无位置传感器控制［D］.沈阳:沈阳工业大学，2005:36－340.

［9］ RIBEIRO L A S，DEGNER M W，BRIZ F，et al.Comparing carrier frequency current and voltage injection of the estimation of flux，position，and velocity in sensorless AC drives［C］//IEEE，IAS Conf.Rec.1998:452－459.

［10］ 刘家曦.无传感器内嵌式永磁同步电机转子磁极位置检测技术研究［D］.哈尔滨:哈尔滨工业大学，2010:36－37.