百慕大可转债的最优转换策略
宋丽平
(莆田学院 数学学院,福建 莆田 351100)
百慕大可转债的最优转换策略
宋丽平
(莆田学院 数学学院,福建 莆田 351100)
本文研究一个可以在n个离散时点上进行转换的百慕大可转换公司债券(简称可转债)模型.采用基于公司价值的可转债定价模型,在公司风险资产的价值遵循几何Brown运动,且股价具有稀释效应的情形下,对百慕大可转债的最优转换策略进行分析.研究结果表明,存在一个非负的常数临界值,当公司风险资产价值高于这个临界值时,可转债应转换;否则,不转换.
百慕大可转债;最优转换策略;稀释效应;几何Brown运动;无套利定价理论
0 引言
可转换公司债券(简称可转债)的持有者可以选择在规定的期间内按事先约定的价格转换成发行公司的股票,也可以选择持有至到期日,要求公司还本付息.因此可转债是一种具有债权性和期权性双重性质的混合型金融工具.
按可转债持有者执行的时限划分,可转债可分为欧式可转债、百慕大可转债和美式可转债.对于欧式可转债,主要采用Black和Scholes[1]和Merton(1973,1974)[2-3]关于期权及公司债券的定价模型.Ingersoll[4]和Brennan & Schwartz[5]最早采用基于公司价值的可转债定价模型,他们假设公司价值遵循几何Brown运动,可转债的价值只与公司价值有关,并在Black & Scholes的框架下对可转债进行定价.最早建立了以股票价格为变量的可转债定价模型的是Mc Connell & Schwartz[6],即在股票价格遵循几何Brown运动的情形下,假设可转债的价值只与股票价格有关,由此利用Black & Scholes模型对可转债进行定价.百慕大可转债的持有者可以在到期日之前的若干时点上进行实施,它介于欧式可转债和美式可转债之间.目前,对于百慕大可转债的定价问题,以二叉树和蒙特卡罗模拟方法为主,相关的理论研究还比较少.化宏宇和程希骏[7]对二期百慕大权证进行定价,即存在2个可行权日:事先规定好的某一特定日期和到期日,首先在Black和Scholes模型的基础上,分析了敲定价格为K、到期日为T的标准欧式期权在0时刻的价格,再进一步推导其在0时刻的价格.
此外,可转债与看涨股票期权不同,主要体现为实施后股价是否稀释了.因为看涨股票期权实施时的股票已经在金融市场上流通了,所以看涨股票期权的实施不会引起股票数量的增加,从而股价不会被稀释.因为公司不能持有自己的股票,所以可转债实施时,公司必须发行新的股票,股票数量增加,引起股价的变化,即稀释效应.因而,在研究可转债的最优实施策略及其定价问题,必须考虑股票的稀释效应,否则,定价就会与实际的金融市场产生较大偏差.
本文将在一个任意给定的有限个离散时间点上均可以实施的百慕大可转债模型下,采用基于公司价值的定价模型,并考虑股价的稀释效应,对百慕大可转债的最优转换策略进行研究.
1 模型
设市场是完备的(如无交易费等等)和无套利的,(Ω,G,=(Gt)0≤t≤T,P)为带σ-代数流的完备的概率空间,满足通常的条件,其中Gt表示直到时刻t为止所获得的信息,Gt=σ(Zs,0≤s≤t).
假设公司通过发行股票和可转债来融资,在时刻0发行M份可转债和N份股票.公司资产结构如下:
公司总资产=公司风险资产+公司无风险资产=股票+可转债
(1.1)
可转债持有者根据股票价值和可转债价值的大小关系选择转换策略,若股票价值大于可转债价值,则转换成股票;否则不转换.若在到期日T可转债没有被转换,则在时刻T每份可转债可获得R的支付.考虑一个可以在n个时点上实施的百慕大可转债模型,其可实施时刻为tn,tn-1,…,t2,t1,其中0=tn+1 图1 n期百慕大可转债(圆点“·”表示可实施时刻) 由(1.1),有 Vt+L0ert=NSt+MDt,0=tn+1≤t (1.2) (1.3) 其中mti表示时刻ti的转换量,mti=0,M(i=1,2,…,n),Vt、Dt和St分别表示时刻t公司风险资产的价值、可转债的价值和股票的价值,L0为公司无风险资产的初始价值,r为无风险利率. 由于可转债转换时,会使市面上流通的上市公司的股票数量增加,引起股票价格的变化(稀释效应),即股价变化不再遵循几何Brown运动.本文采用基于公司价值的可转债定价模型,并假设公司风险资产的价值遵循几何Brown运动,可转债的价值只与公司价值有关.此外,不考虑违约情形,即假设公司价值足以支付在到期日T没有被转换的可转债的面值.设Q为与P等价的鞅测度(风险中性测度),在Q下,公司风险资产价值遵循如下过程: dVt=Vt(r-δ)dt+VtσdZt,0≤t≤T. (1.4) 其中δ为分红率,σ为波动率,Zt为标准Brown运动,且r,δ,σ均为正常数. 本节研究百慕大可转债的最优转换策略,考虑股价的稀释效应,即可转债转换为公司股票后,会使公司股票的数量增加,引起股价下跌. 对k=1,2,…,n,设可转债在时刻tk之前没有转换,即mti=0(i=1,2,…,k-1),以Stk表示时刻tk转换之后(即mtk=M)对应的股票价格.设在时刻tk可转债还没有转换(即可转债还存在,这时mtk=0),用Dtk表示时刻tk的可转债价格,其中Dt1≡R. 由(1.3)知, Vtk+L0ertk=(N+M)Stk(Vtk),k=1,2,…,n. (2.1) 为了研究最优转换策略,需要比较在可转换时刻tk(k=1,2,…,n)的股票价格(须是转换之后的价格)Stk与Dtk的大小关系,为此令 fk(Vtk)≡(N+M)(Stk(Vtk)-Dtk(Vtk)),k=1,2,…,n. (2.2) 则由(2.2)知,当fk(Vtk)>0(k=1,2,…,n)时,在可转换时刻tk(k=1,2,…,n)应实施转换;否则不转换.又由(2.1)-(2.2),有 fk(Vtk)≡Vtk+L0ertk-(N+M)Dtk(Vtk),k=1,2,…,n. (2.3) 引理2.1fj(Vtj),Dtj(Vtj)(j=1,2,…,n)具有如下性质: fj(Vtj)∈C1(0,+∞) (2.4) (2.5) (2.6) (2.7) (2.8) Dtj(Vtj)∈C1(0,+∞) (2.9) (2.10) 其中导数除了个别点外均存在,Cj(j=1,2,…,n)表示不同的正常数. 证明(利用数学归纳法)当j=1时,由(2.3)和Dt1≡R,(2.4)-(2.10)显然成立. 假设当j=k时,(2.4)-(2.10)成立,下证当j=k+1时,(2.4)-(2.10)也成立. 由无套利定价理论[8], Dtk+1(Vtk+1)=e-r(tk-tk+1)Etk+1[max(Stk,Dtk)] 将(2.2)代入上式, (2.11) 由于(2.4)和(2.8)-(2.10)对j=k成立,因而由(2.11),知(2.9)-(2.10)对j=k+1成立.结合(2.3)和(2.10),易知(2.8)对j=k+1成立.下证(2.4)-(2.7)对j=k+1成立,分为两种情形来证明. 10当L0ert1-(N+M)R<0时,由于(2.4)-(2.7)对j=k成立,因此,存在唯一的正常数λk,使得 (2.12) 由(2.11)及(2.8)和(2.10)对j=k成立,有 (2.13) 又由(2.12), (2.14) 由(2.3), (2.15) 由(1.4)知,e-(r-δ)tVt是Q-鞅,因此 Etk+1[Vtk]=e(r-δ)(tk-tk+1)·Vtk+1 (2.16) 将(2.16)代入(2.15)得, (2.17) 由(2.17)、(2.5)和(2.16), (2.18) 再由(2.3)和(2.18), (2.19) 即(2.4)-(2.5)对j=k+1成立. 类似于(2.17)的证明,由(2.3)和(2.11),可得 (2.20) 从而(2.6)-(2.7)对j=k+1成立. 20当L0ert1-(N+M)R≥0时,λk=0. 由(2.20), fk+1(Vtk)=Vtk+1(1-e-δ(tk-tk+1)) (2.21) 由(2.21),易知(2.4)-(2.7)对j=k+1成立. 定理2.1在可转换时刻tk(k=1,2,…,n),百慕大可转债的最优转换策略为 其中常数λk满足: 证明当L0ert1-(N+M)R<0时,由引理2.1中的(2.5)-(2.7)知,对k=1,2,…,n,存在唯一的正常数λk,满足 即λk>0,且λk是方程fk(Vtk)=0的唯一解. 再由可转债的定义,可得其最优转换策略为 本文研究百慕大可转换公司债券(可转债)的最优转换策略问题.按照可转债的定义知,在可转换时刻tk(k=1,2,…,n),若Stk>Dtk(Dt1≡R),则转换;否则不转换. 本文的研究结果表明,在可转换时刻tk(k=1,2,…,n),若Vtk>λk(λk为某一非负常数),则转换;否则不转换. 也就是,下述等价关系成立: Stk>Dtk(Dt1≡R)⟺∃常数λk≥0,s.t.Vtk>λk,(k=1,2,…,n) (3.1) [1]F.Black,M.Scholes.The Pricing of Options and Corporate Liabilities[J].Journal of Political Economy,1973,81(3):637~654. [2]R.Merton.Theory of Rational Options Pricing[J].Bell Journal of Economics and Management Science,1973,4(1):141~183. [3]R.Merton.On the Pricion of Corporate Debt:The Risk Structure of Interest Rate[J].The Journal of Finance,1974,29(2):449~470. [4]J.Ingersoll.A Contingent-claims Valuation of Convertible Securities[J].Journal of Financial Economics,1977,4(3):289~321. [5]M.J.Brennan,E.Schwartz.Convertible Bonds: Valuation and Optimal Strategies for Call and Conversion[J].The Journal of Finance,1977,32(5):1699~1715. [6]J.Mc Connell,E.Schwartz.LYON Taming[J].The Journal of Finance,1986,41(3):561~576. [7]化宏宇和程希骏.分离交易可转债研究[J].中国科学院研究生院学报,2008,25(4):439~444. [8]T.Bjork.Arbitrage Theory in Continuous time,Second Edition[M].Oxford university press,Oxford,2003. TheOptimalConversionStrategiesforBermudaConvertibleBonds SONGLi-ping (School of Mathematics,Putian College,Putian 351100,China) This paper is concerned with the model of Bermuda convertible corporate bonds (convertible bonds for short) with n discrete conversion times.By use of the pricing model of convertible bonds based on the company's value,the optimal conversion strategies for Bermudian convertible bonds are analyzed in the case when the value of the company's risk asset follows a geometric Brownian motion and the stocks have dilution effect.Results confirm that there is a non-negative constant threshold.Moreover,when the company's risk asset value is higher than this threshold,convertible bonds should be converted;otherwise,they should not be converted. Bermuda convertible bonds;optimal conversion strategies;dilution effect;geometric Brownian motion;arbitrage-free pricing theory 梁怀学) 2014-03-25 国家自然科学基金项目(1001142);福建省教育厅资助项目(JB12171);莆田学院教学改革项目(JG201316) 宋丽平(1979-),女,福建省莆田市人,现为莆田学院数学学院讲师,博士.研究方向:金融数学. O211.6;F830.9 A 1674-3873-(2014)03-0075-04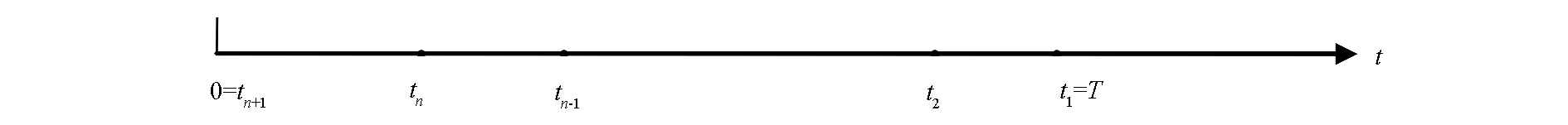
2 最优转换策略
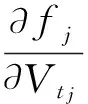
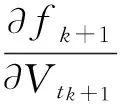
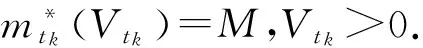
3 结论

