基于GRNN 的霍尔式位移传感器特性曲线拟合研究

丁 硕,常晓恒,巫庆辉

（渤海大学工学院，辽宁锦州，121013）

0 引言

本文提出了利用GRNN 对霍尔式位移传感器的输入-输出特性曲线进行拟合的新方法，并利用LM (Levenberg-Marquart)算法对传统BPNN 进行改进，在MATLAB7.0 环境下，编程实现两种神经网络，分别对霍尔式位移传感器的特性曲线进行拟合，并对拟合结果进行比较分析。仿真结果表明，相对于BPNN，GRNN 的拟合精度更高，且收敛速度更快。

1 霍尔式位移传感器的工作原理概述

霍尔式微位移传感器在实际微位移测量场合中得到广泛应用，它的工作原理主要基于霍尔元件的霍尔效应。一块长方形金属薄片或半导体薄片，若在某方向上通入电流I，在其垂直方向上加一磁场B，则在垂直于电流和磁场的方向上将产生电位差VH，VH =KH I B，这个现象称为霍尔效应，式中VH 称为霍尔电势，K H 称为灵敏度系数。由上式看出，霍尔电压VH 的大小和电流I、磁场

强度B 成正比。霍尔元件的厚度越小，灵敏度系数越高，但霍尔元件的机械强度下降、输入、输出电阻增加。另外，因为很多霍尔元件由半导体材料制成，半导体材料对于温度较为敏感，霍尔式传感器的输入电阻、输出电阻、灵敏度系数也随着温度发生改变，所以会对测量精确度产生影响。但只要霍尔式微位移传感器工作在正常条件下，保持电流I 为常数，则霍尔电势VH 与被测试件位移S 之间就会呈现线性比例关系。若被测试件带动霍尔元件在一个均匀磁场中移动时，霍尔电势VH 变化就直接反映被测试件位移S 的情况。正是基于这一原理霍尔式微位移传感器可以对被测试件位移量进行检测。

2 仿真实验

本文实验中采用型号为A3144 的霍尔式位移传感器，完成系统硬件连接，并对系统进行调试,采用机械放大杆并配合使用杠杆千分尺的形式来获得被测磁钢的位移信号，磁钢的位移由千分尺读出。在标准室温条件下，并在A3144 传感器测试量程允许范围内，采用正反行程（正向行程、反向行程各10 次）多次测量最后取平均值的方法获得传感器的输出电压与被测位移量之间的测量数据。由实验数据可知:输出电压与被测位移量之间的变化趋势在被测磁钢位移量较小时基本上成线性关系；但是在被测磁钢位移量较大时,线性度较差，呈现非线性关系,这主要是因为影响传感器输入-输出特性的因素有很多：被测磁钢所提供的磁感应强度存在非线性、表面磁效应、表面镀层及传感器的安装和工作温度等诸多因素都会对霍尔式位移传感器的特性产生影响。在MATLAB7. 0 环境下，将实验测得数据进行归一化处理，将所测得的数据映射到指定的区间[0,1]中，编程建立GRNN和BPNN，对网络初始化并分别进行训练，霍尔式位移传感器输入位移量变化范围：0.000-8.000cm；输出电压变化范围：0.000-5.820V。

2.1 GRNN 和BPNN 的建立

在建立GRNN 时，只需要选择一个合适的径向基函数的分布密度SPREAD 值，SPREAD 值的大小对于网络的拟合结果影响很大，SPREAD 的值越小，神经网络对样本数据的逼近性就越好；SPREAD 的值越大，神经网络对样本数据的拟合结果就越光滑，但与此同时网络输出误差会增大。文中在MATLAB7.0 环境下编写GRNN 算法程序进行非线性函数逼近研究，SPREAD 分别取0.05，0.5，1.0，3.0，5.0，程序采取循环训练算法，不同SPREAD 值对拟合结果的影响如图1 所示。可以看出，当SPREAD=0.05 时，文中所建立的GRNN 达到最佳拟合效果。

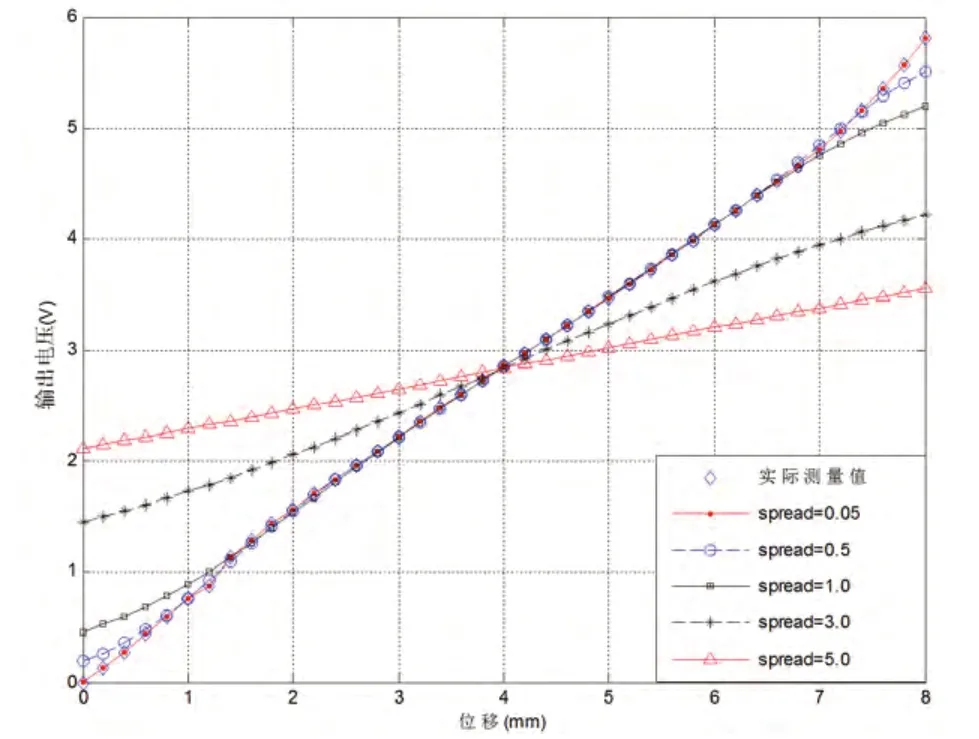
图1 不同SPREAD 值对拟合结果的影响

因为传统的BPNN 收敛速度慢，逼近精度不够高，文中利用LM 算法对BPNN 进行改进。建立LM-BPNN 主要包含网络层数、隐层神经元个数、初始权值和学习率四个要素。文中在对测量数据进行拟合时，BPNN 采用单隐层结构；由于隐含层的神经元数目的冗余将使网络庞大，训练困难，而不足又会导致训练失败，所以文中采用动态法最终确定最佳隐含层神经元数为13。文中在建立LM-BPNN 时，输入值在加权处理后尽可能接近零，这样可以保证初始权值的调整发生在S 型传递函数的斜率最陡处。为了兼顾系统稳定性和具有较快的收敛速度，文中学习率选取为0.1。

2.2 GRNN 和BPNN 的整体拟合结果对比

在样本数和精度要求相同的条件下，分别用GRNN 和BPNN 对霍尔式位移传感器的测量数据进行拟合，两种网络对测量数据的绝对误差变化曲线如图2 所示，由图2 可以看出，GRNN 对于各个测量点拟合的绝对误差比BPNN 小很多。如果要进一步提高BPNN 拟合精度，可以通过增加隐层单元数或选择多个隐层结构网络的方法，但这样很容易导致拟合的局部振荡，会影响网络的泛化能力。相比之下，GRNN 对测试数据几乎达到了完全逼近，只有个别测试数据有较小误差，但最大绝对误差不超过1.5258e-007；BPNN 有较大误差，且误差波动较大，其最大绝对误差不超过-0.0250。

图2 BPNN 与GRNN 的绝对误差变化曲线

分别用GRNN 和BPNN 对测量数据进行仿真，两种网络对于霍尔式位移传感器的拟合效果如图3 所示。由图3 可以看出，两种网络都实现了对霍尔式位移传感器特性曲线的拟合。GRNN 在传感器测量范围内几乎做到了完全逼近，且GRNN 拟合曲线更平滑，而BPNN 在多个测量点上仍存在逼近相对误差大、逼近效果不理想的现象。在样本集数目和精度要求相同的条件下，GRNN和BPNN 对于霍尔式位移传感器的输入-输出特性曲线的整体拟合结果对比如表1 所示。由图3 可以看出，GRNN 拟合结果的均方误差远远小于BPNN 拟合结果的均方误差，BPNN 的均方误差为9.3746e-005，而GRNN 的均方误差只有7.1550e-013，两者不在同一数量级。GRNN 拟合的收敛时间也远小于BPNN 的收敛时间，BPNN 的收敛时间为1.0019s，而GRNN 的收敛时间只需要0.0410s。可以得出结论，在对霍尔式位移传感器的测量数据进行拟合时，GRNN 的综合性能较BPNN 更为优越，GRNN 在整体拟合效果上要优于BPNN。

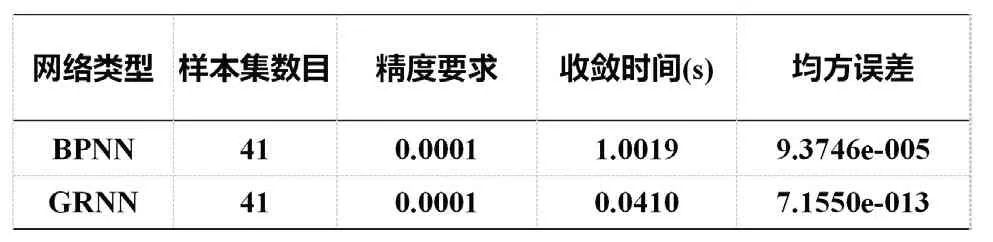
表1 BPNN 与GRNN 整体拟合结果对比

3 结语

GRNN 和BPNN 对训练样本均有很高的拟合精度,但相比之下，GRNN 在逼近能力和学习速度上较BPNN 有更强的优势，并且在样本数据较少以及存在不稳定数据时，拟合效果也同样较好，而BPNN 则需要更多的训练样本。BPNN 需要手动调整网络结构，设计起来较为复杂，而GRNN 设计起来更方便，这就最大限度地降低了人为主观因素对逼近结果的影响。

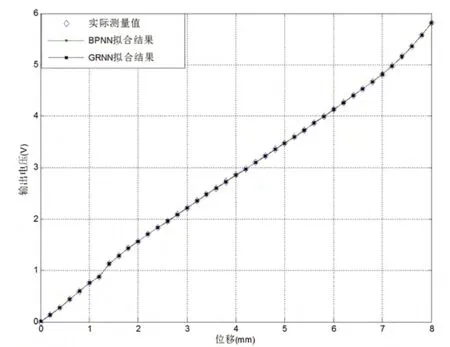
图3 BPNN 与GRNN 对于霍尔式位移传感器的拟合效果

[1] 丁硕，常晓恒，巫庆辉.LMBP 和RBF 神经网络在ECS 特性曲线拟合中对比研究[J].吉林大学学报（信息科学版），2013，31 (2)：203-209.

[2] 黄忠明，吴志红，刘全喜.几种用于非线性函数逼近的神经网络方法研究[J].兵工自动化，2009, 28（10）：88-92.

[3] 丁硕，巫庆辉.基于改进BP 神经网络的函数逼近性能对比研究[J]. 计算机与现代化， 2012， 11： 10-13