基于VB 语言的分形图的计算机生成与应用
帅昌浩
浙江农林大学暨阳学院
分形图应用广泛,越来越受到大家的重视。本文对生成分形图的常见算法作了简单介绍,并利用VB 语言设计开发了分形图的生成软件,并将生成的分形图加以适当的图形处理后应用到实际生活中去。
引言
分形理论是近四十年才发展起来的一门新兴学科。首先由美国哈佛大学数学系教授Mandelbrot 在1975年提出,隶属于非线性理论。计算机的飞速发展给分形理论的研究插上了腾飞的翅膀,其应用十分广泛。如今分形图越来越多地被应用在家具、服装、包装和标识等行业的图案设计中。
分形图的生成算法
由于分形图非常精细,结构非常复杂,很难用手工来绘制。必须借助计算机来实现。根据分形图的特点,常用算法主要有递归法、文法构图法、迭代函数系统等。下面对这几种算法作简单介绍。
递归法
分形图具有自我相似、自我复制、自我嵌套的特点,由数学上的递归算法利用计算机中压栈和出栈的功能,重复使用某些规则来生成嵌套的结构,从而逐步细化图像细节而得到最终结果,像经典分形图形cantor 三分集、koch 曲线、sierpinski 地毯等都可由递归算法得到。递归算法生成分形图形的过程简单易懂,而且形状特征和迭代过程明显的分形图都可以用这种方法得到 。
文法构图法(LS 文法)
文法构图法是仿照语言学中的语法生成方法来构造图形的一种方法。LS 文法是由美国生物学家Lindenmayer于1968年提出的一种文法构图法,制定一个或几个初始字母和一组“生成规则”将生成规则反复作用到初始字母和新生成的字母上,产生出整个语言。例如:字母表L R;生成规则:L →LR,R →L;初始字母R;则有R →L-→LR→LRL→LRLLR→LRLLRLRL→……,由此可见,文法构图法灵活多变,初始字母和生成规则变了,分形图就变了。像形态各异的分形树,Hilbert-Peano 曲线,龙曲线等都可用此算法生成。
迭代函数系统(IFS)
美国科学家M.F.Bansley 于1985年发展了自相似集这一分形构型系统,并命名为迭代函数系统,是分形图形图像处理中最富生命力并具有广泛应用前景的领域之一。IFS 方法是一种基于分形的,采用点的构造模型的方法。采用拼贴的思想将生成的图像看成是由许多与整体相似的或经过一定变换与整体相似的小块拼贴而成。像C 曲线、鱼群、圣诞树灯都可用此算法来生成。
除了上述常见的分形算法以外,在绘制分形图形中常见的还有分形的逃逸时间算法、元胞演化法等等,这里就不再一一介绍了。
分形图生成软件设计
由前面介绍的分形算法,编写程序代码,在计算机上就能生成绚丽多彩的分形图,再修改程序代码中的若干参数,分形图的形状更具灵活性和多样性。如生成Sierpinski 垫片的递归过程VB 程序代码为:


在计算机上运行就生成一颗蓬勃生长的分形树。

当然可以通过参数的修改使得分形数的形态各异。为了使分形图更好地应用到实际生活中去,可以基于VB 语言设计一个分形图生成软件。其用户界面如下图所示。
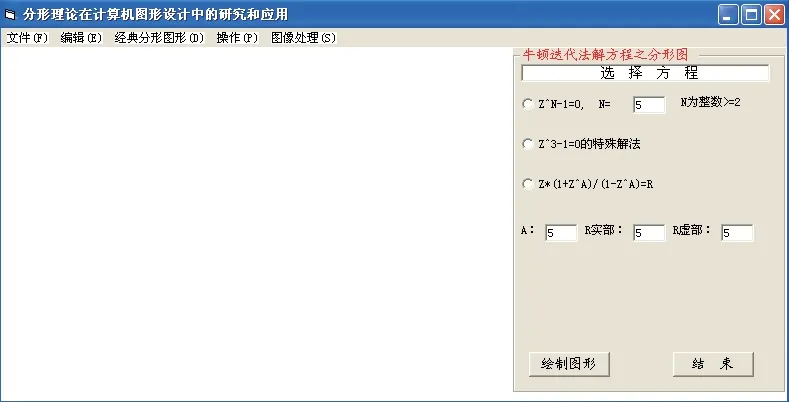
使用该软件可以生成需要的一些分形图形,软件里还有图像处理按钮,可以将生成的分形图或其它图形进行合成、翻转、特效等处理。这样处理后的图形更加实用,如Mandelbrot 集和分形树的合成图像。

对分形图浮雕特效处理后的图像为

分形图在现实生活中的应用
用分形软件生成的分形图形还是比较粗糙的,如果用图形处理软件做一定处理其应用将更加广泛,效果也更加好。可以为工业图案设计提供素材,可以制作成各种尺寸的精美装饰画,制作分形服装。还可以将其应用于印染行业,广告图案设计,包装材料图案等领域中。如分形服装设计。

装饰画设计

标志标识设计,下面是谷歌公司某一期的标志。
结语
分形图形具有其独特的魅力,深受大家的喜爱。但对它的研究尚处于发展阶段,尚待分形爱好者和专业人士去更深入地探索和研究。不可否认分形图形的应用是十分广泛的,在现实生活中的方方面面会出现越来越多的分形图形。

