一种基于飞机目标CFD图的目标特征提取算法研究
姜卫建,姜 悦
(1.陕西黄河集团有限公司, 西安710043;2.西安电子科技大学电子工程学院, 西安710071)
0 引言
由于现役的常规对空警戒雷达基本上都属于窄带雷达,其距离分辨单元尺寸远远大于目标尺寸,目标的雷达回波可以近似看作是点目标的回波。相对于利用低分辨窄带雷达搜索目标,同时再配合高分辨宽带雷达进行目标分类识别的工作方式,直接在低分辨窄带雷达中加入目标分类识别功能,不仅可以节约高分辨宽带雷达带来的系统复杂度,而且还可以最大限度地发挥现有低分辨窄带雷达的作战效能。以上现实造成了简单的利用雷达回波单一维度信息进行分类识别已经是远远不够了,为了从低分辨雷达回波中提取更多更有效的分类信息,本文研究了一种基于飞机目标空间微动部件微多普勒回波时频二维数据的目标分类识别算法——韵律频率图(Cadence Frequency Diagram,CFD)分类算法[1]。CFD分类算法利用目标回波短时傅里叶变(STFT)[2]后得到的时频信息,从中提取特征对飞机目标进行分类,比单纯的使用目标回波时域或频域一维信号提取特征包含了目标更多的信息量,能够更好地实现目标分类。
1 飞机目标回波时频图
利用飞机发动机旋转部件回波模型仿真雷达回波,具体表达式如下

式中:M1、M2分别表示受飞机桨叶角调制的相关系数。在对雷达接收到的目标回波信号进行脉冲压缩、补偿速度修正目标多普勒频移影响,并去除地物累加杂波等一系列处理之后,利用短时傅里叶变换(STFT)就可以得到目标回波的时频图(TFD,Time-Frequency Diagram)。图1描述了仿真直升机目标的时域、频域雷达回波,图2则描述了经短时傅里叶变换(STFT)后得到的直升机目标雷达回波的时频图。

图2 仿真直升机旋翼回波时频图
图2a)中的类正弦部分为直升机旋翼的微多普勒频谱,纵贯的直线表示了直升飞机目标空间微动部件的雷达回波在时间域上出现的闪烁,只有当雷达视线与飞机空间微动部件的旋翼垂直时才会出现。观察图2a)在已知旋翼桨叶数的情况下可以从时频图中得到旋翼的旋转周期T=0.25 s,进而推算出旋翼转动的角速度ωr=25.13 rad/s,而实际仿真的直升机旋翼旋转角速度ωr-ture=242 rad/min=25.34 rad/s。直升机旋翼回波的单边谱宽

由此再根据已知的雷达参数就可以推导出直升机旋翼其他相关的物理信息。
2 CFD特征提取算法
目标回波的时频图包含了飞机目标旋翼部件的特征信息,这些信息对于区分不同类型的目标有着十分重要的作用。然而,时频图庞大的数据量造成了直接输入分类器分类时分类器的复杂度过高往往无法实现。为了利用时频信息进行目标分类,就需要对时频图进行降维,得到一个维数更少的“特征向量”。
一种改进时频图的飞机空间微动部件目标基于CFD特征提取算法就是一种对飞机目标时频图进行“降维”改进的时频图特征提取的算法。所谓的CFD图是由目标回波的时频图(TFD)沿时间维的再次傅里叶变换得到的。目标回波的CFD图形象地表示了不同频率成分出现的频次(故此可以称时频图沿时间维傅里叶变换后的Cadence Frequency维度为韵律频率维),此时的韵律频率不仅包含了时频图中目标空间微动部件微多普勒回波相关曲线的形状、尺寸和频率信息,并且就信息散布程度而言更为集中。图3所示为仿真直升机回波的时频图以及对应的CFD图。

图3 仿真直升机时频图和CFD图
观察仿真直升机的CFD图可以发现有效信息只集中在韵律频率中心频率附近的一定范围内,并且在频率维同时频图一样关于零频对称,而CFD图的其余部分信息量极少。根据这一特点,为了保证特征能够包含目标本质物理运动信息的同时尽可能的降低特征维数,减少分类器复杂度,本特征提取算法仅利用了CFD图中最强的两次回波部分作为特征向量,具体特征提取算法可以概括为如下步骤:
(1)利用短时傅里叶变换得到目标回波的时频图;
(2)沿时间维对步骤(1)的时频图进行傅里叶变换得到目标回波的CFD图,其中CFD图可以表示为
(3)在CFD图中沿原始的频率维求和(图4a));
(4)求和后选择其中最强的M=2个韵律频率(Cadences Frequency)峰值;
(5)对于所选中的各个 m={1,2,…,M}韵律频率在CFD图中确定相应的峰值cm和对应的频率剖面fm(图4b));
(6)标准化cm与fm:
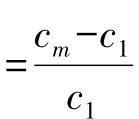
对数标准化fm:=lg(fm-lg max(fm);
(7)得到最终的特征向量 x=[c1,c2,…,cMf1,f2,…,fM]∈A1×N。
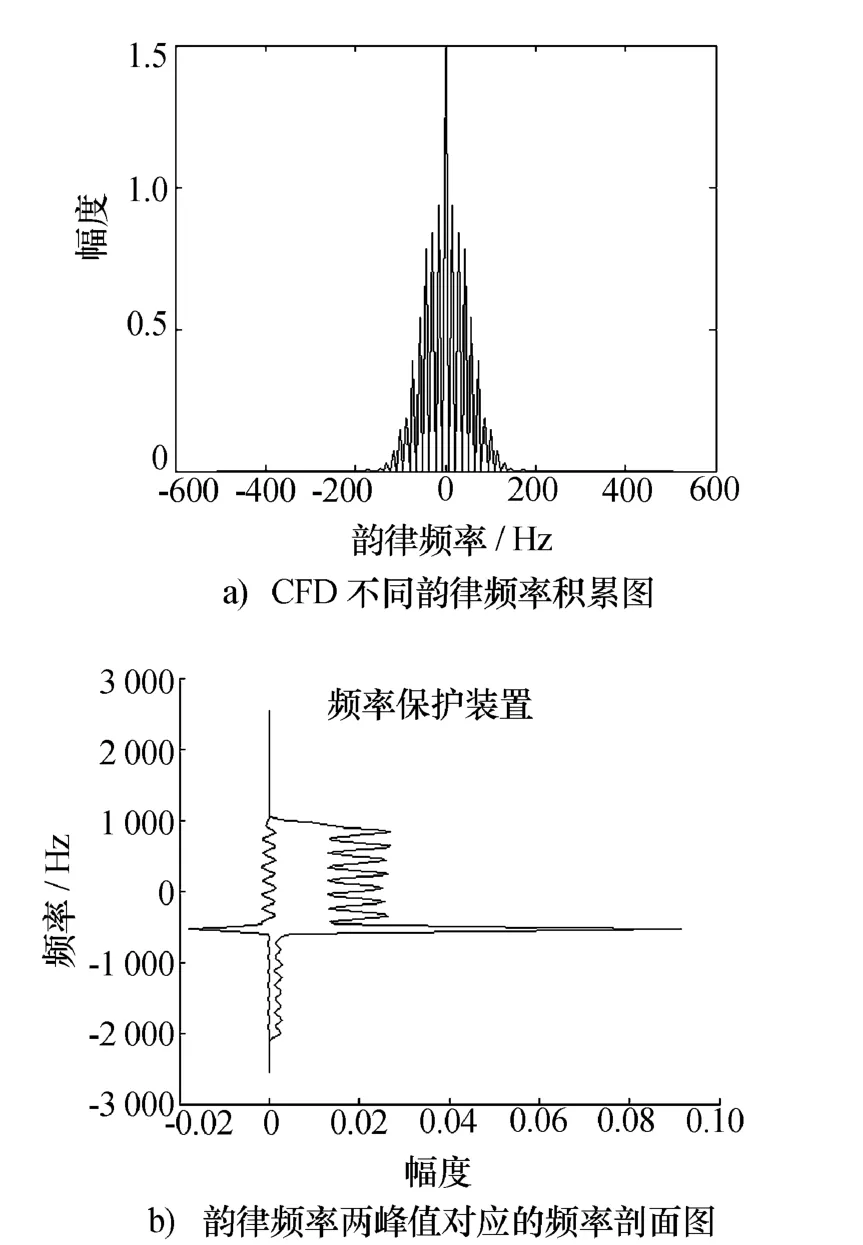
图4 CFD特征提取算法说明
图4分别反映了CFD特征提取算法步骤(3)和步骤(5)所对应的特征向量。图4a)为CFD图沿频率维方向由上至下求和得到的幅度积累韵律频率(Cadence Frequency,C-F)图。因为 Sum over frequency(图4a))关于零频对称,所以在其中找到正韵律频率最大的两个C-F频率的位置,并在相应位置处对CFD图沿Frequency维切片就得到了图4b)。
3 仿真实验及分析
仿真实验采用4 kHz雷达重频下产生数据的输入SVM分类器进行目标分类识别,训练数据和测数据数采用不同型号的三类飞机参数,环境参数由表1随机产生。飞机型号参数均由表2到表3随机组合选取,其中训练数据三类飞机各为210组,测试数据三类飞机各为100组。

表1 直升机仿真参数(L1=0 m)

表2 螺旋桨飞机仿真参数
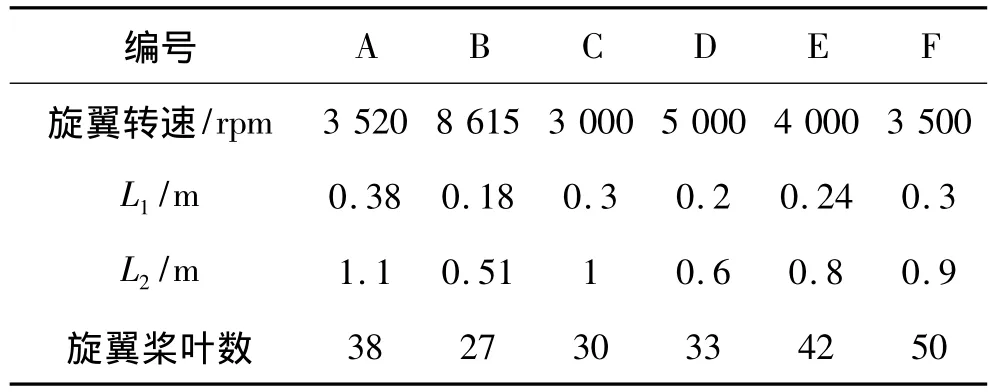
表3 喷气式飞机仿真参数
图5的a)、c)、e)分别展示了仿真直升飞机、螺旋桨飞机、喷气式飞机三类飞机目标的时频图;而图5的b)、d)、f)分别展示了仿真三类飞机目标回波对应的CFD图。
最后就是得到实际输入分类器的分类特征,只要根据找到的最强和次强韵律频率得到对应的频率切片即可。

图5 仿真三类飞机数据的时频图和CFD图
由上一节飞机目标CFD特征提取算法可知,在得到目标回波的CFD图之后,对其做切片得到最大的两个峰值所对应的频率切片即为本章最终用来区分三类飞机目标的特征向量。图6分别描述了仿真直升飞机、螺旋桨飞机和喷气式飞机目标最终输入分类器的CFD特征向量。
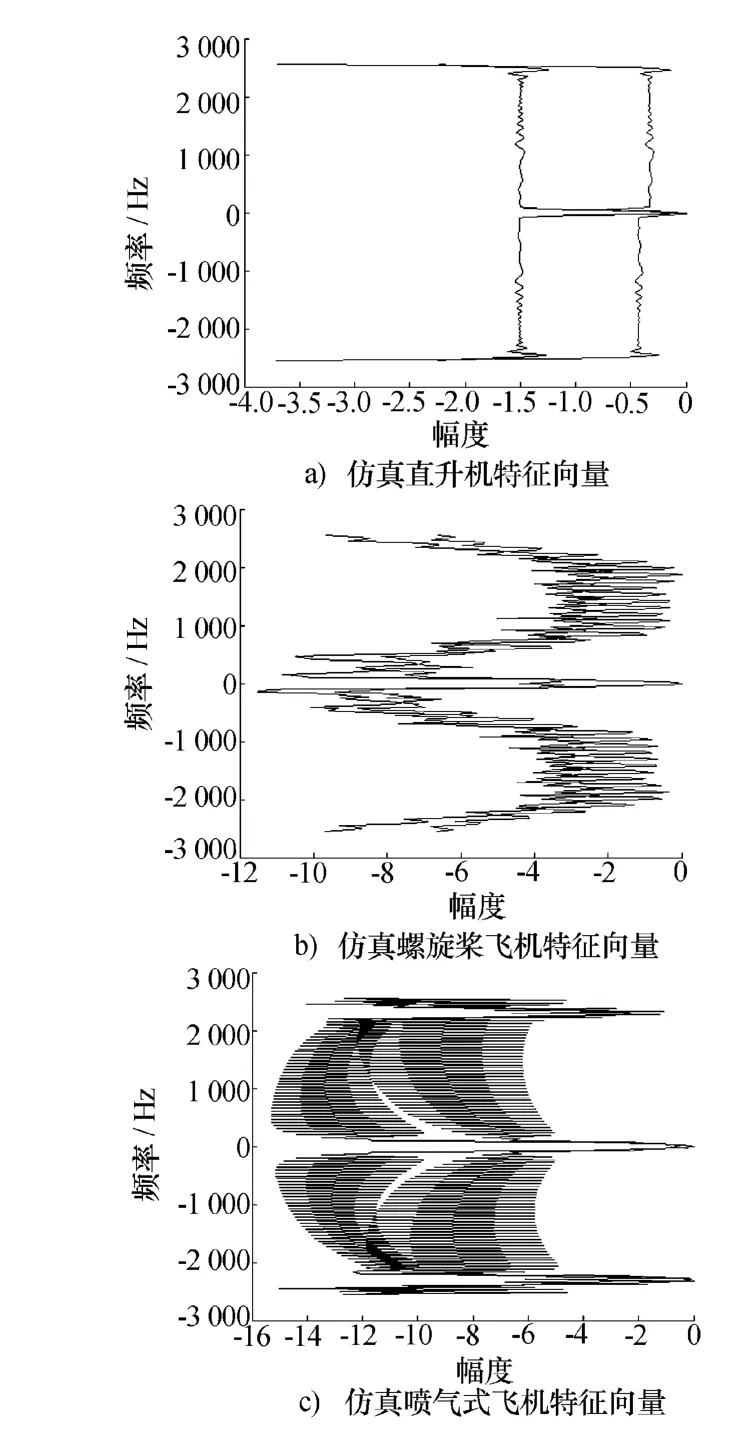
图6 仿真三类飞机目标的CFD特征向量
CFD特征已经是对飞机目标时频图进行降维后得到的“低维”特征,从图6中可以看出不同类型飞机目标的CFD特征向量之间存在明显差异,直升飞机的切片幅度变化平缓,且幅度均较大;螺旋桨飞机切片的幅度在零频附近有着明显的凹陷,而在两端频率处幅度在较大值附近存在一定波动;喷气式飞机除了在零频处有峰值外,在频率两端也存在窄频宽的峰值,而其他区域均存在幅度较低的明显起伏。为了更直观地描述CFD特征对三类飞机目标的分类效果,我们通过主成分分析[3](Principal Component Analysis,PCA)对其进行降维,取降维后的前两维主分量代表CFD特征,并画出这前两维特征的散布图来表征CFD特征在特征分类平面上的分布情况。
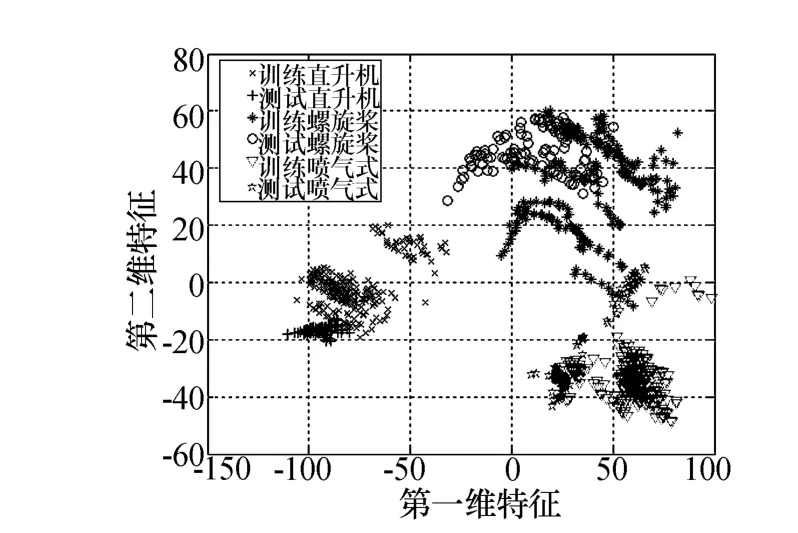
图7 仿真数据CFD特征第一维和第二维主分量特征散布图
对于仿真的三类飞机目标空间微动部件而言,CFD特征有着明显的分类识别优势。将上述630组仿真训练数据输入SVM分类器,300组仿真数据进行测试,可以得到表4所示的分类识别结果。
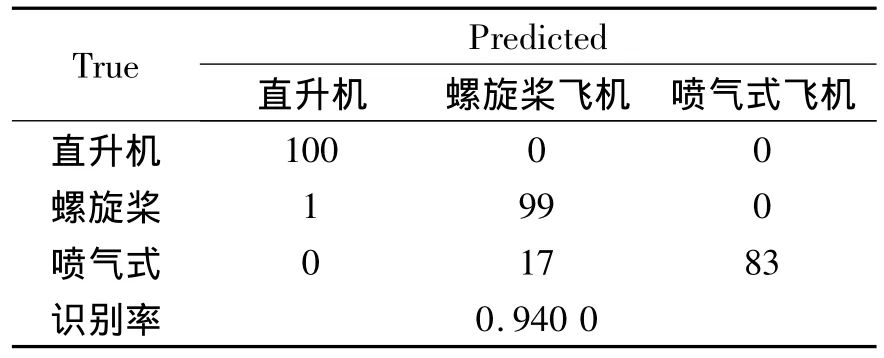
表4 仿真数据分类结果的混淆矩阵
4 相关参数对CFD特征的影响
4.1 信噪比
表4所述的实验中训练数据及测试数据均未加入噪声影响,但在实际情况下噪声是无法避免的存在,任何雷达接收到的目标回波中均包含噪声。因为CFD特征在提取特征向量时存在两次傅里叶积累,所以CFD特征对于噪声而言是不敏感的。为了能够直观的观察CFD特征对三类飞机目标的识别率随信噪比SNR的变化情况,做了如下实验:
雷达参数:雷达载频为1.3 GHz,雷达重频为5.1 kHz,驻留时间为200 ms;
飞机参数:仿真训练数据,目标回波中加入高斯白噪声,信噪比SNR=10 dB;仿真测试数据,目标回波中同时加入高斯白噪声,信噪比SNR从0 dB~30 dB等间隔选取。

图8 仿真数据CFD特征识别率随SNR变化曲线
观察图8可以发现,在信噪比0 dB~5 dB时CFD特征的识别率较低,在5 dB时接近75%,但当信噪比达到8 dB左右时,CFD特征的识别率有了迅速的提高,直接达到了95%左右。同时,在低信噪比区域CFD特征的识别率随着信噪比的升高其增长速度极快。也就是说,CFD特征对于信噪比有一定的要求,但是此特征对于噪声并不敏感,在低信噪比的情况下也能有较高的目标分类识别能力,CFD特征具有一定的抗噪声能力。
4.2 驻留时间
雷达的驻留时间决定了雷达视线在目标方向上停留的长短。只有当雷达视线停留在目标方向上有足够长的时间时,才能保证接收到的雷达回波中包含飞机目标空中微动部件的一个完整的旋转周期。考虑到CFD特征的本质就是利用飞机目标旋翼的微多普勒特性进行分类识别,那么当雷达驻留时间过短,无法收获必要的多普勒周期特征时,CFD特征就完全失效了。图9描述了三类飞机目标的分类识别率随雷达驻留时间的变化曲线,实验参数如下:
雷达参数:雷达载频为1.3 GHz,雷达重频为5.1 kHz,训练数据和测试数据的驻留时间均从10 ms到500 ms等间隔取得;
飞机参数:仿真训练数据,目标回波中加入高斯白噪声,信噪比SNR=10 dB;
仿真测试数据,加入的高斯白噪声如训练数据。
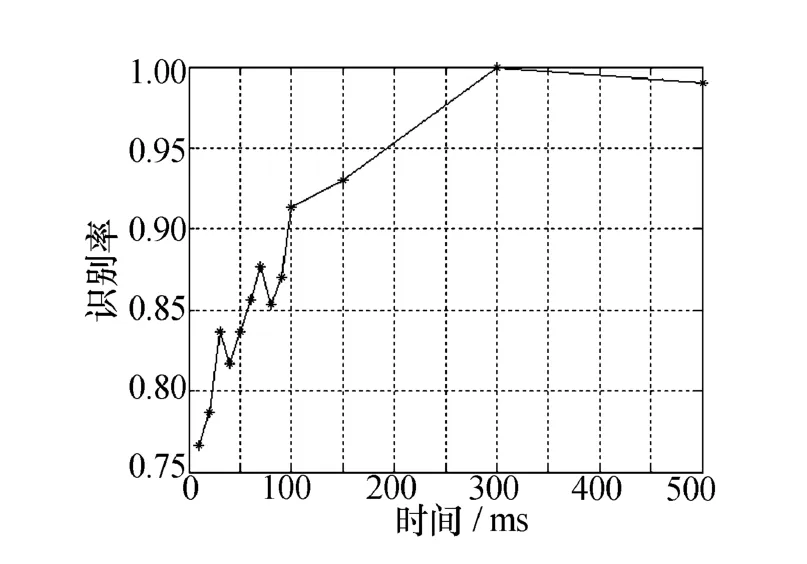
图9 仿真三类飞机目标识别率随驻留时间变化曲线
图9画出了0 ms~500 ms内目标识别率随驻留时间的变化曲线,当测试数据在雷达驻留时间超过一定时间之后其识别率就趋于稳定不再变化了。由于直升飞机桨叶转速慢、桨叶少,当雷达驻留时间在10 ms此种短驻留时间时,即使一个叶片通过雷达视线的完整回波也无法获得,造成直升机类飞机分类错误,直接影响了最终的识别性能。随着雷达驻留时间的增加,此时雷达回波中虽然无法包含完整的目标旋翼周期,但是已经可以取得部分周期信息,因此CFD特征的识别率有了明显提高。当驻留时间达到100 ms附近之后,目标回波已经能够包含完整的旋翼旋转周期,此时依赖CFD特征就已经能够很好的区分三类飞机目标了。
4.3 重复频率
雷达重频决定了雷达回波的方位采样速率,当雷达重频过低时,在某些调制周期内将不能采到回波的闪烁峰值。而更高的雷达重频也对应着更高的雷达回波分辨率,一般情况下也意味着更好的特征识别效果。根据耐奎斯特采样定律,雷达重复频率至少应该大于飞机空间微动部件回波信号频谱带宽的2倍,否则将会发生多普勒谱的混叠,在目标回波的时频图中造成目标信息的失真和损失。
图10描述了CFD特征识别率随雷达重频的变化曲线,具体实验数据如下:
雷达参数:雷达载频为1.3 GHz,雷达驻留时间为100 ms,训练数据和测试数据的雷达重频从1.5 kHz开始到7 kHz等间隔取得;
飞机参数:仿真训练数据,目标回波中加入高斯白噪声,信噪比SNR=10 dB;
仿真测试数据,加入的高斯白噪声如训练数据。
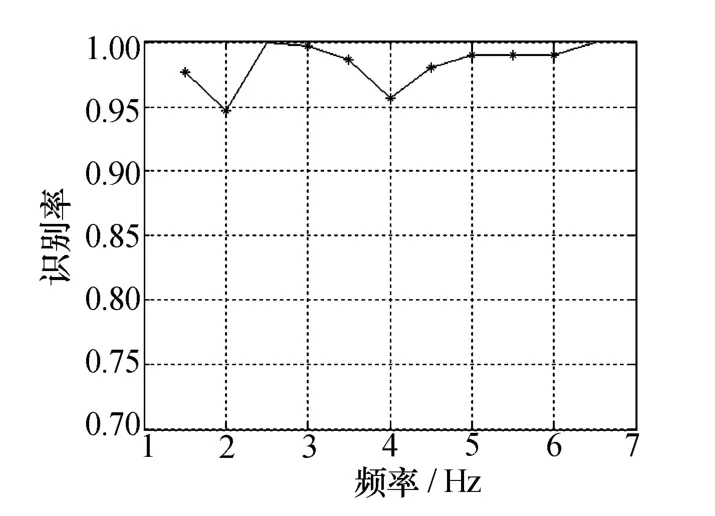
图10 仿真CFD特征识别率随重频变化曲线
观察图10可以发现雷达重频对CFD特征的影响并不明显。过低的雷达重频会造成目标回波频谱发生频率混叠的情况,但是对于CFD特征而言,看重的并不是回波频谱在谱宽内的积累结果,而是提取了某时刻目标回波的所有瞬时频率进行分类识别,因此,雷达重复频率对CFD特征的影响十分有限。
5 结束语
本文主要研究了以目标回波时频图为基础的飞机目标CFD特征提取算法。首先,介绍了短时傅里叶变换,在利用短时傅里叶变换得到的目标回波时频图时,由于短时傅里叶变换的特性,在得到目标时频图时存在一定约束和局限性。接着,研究通过目标回波时频图得到飞机目标CFD特征的特征提取算法,结合CFD特征提取算法中几个重要步骤的图示说明,明确了CFD特征提取算法的各个步骤。通过仿真实验验证了飞机目标CFD特征,在直升机、螺旋桨飞机和喷气式飞机三类飞机目标分类识别中的可行性,同时并验证了此类特征对噪声的稳健性,研究了相关参数对CFD分类特征的影响。
[1] Bjorklund S,Johansson T,Petersson H.Evaluation of a micro-Doppler classification method on mm-wave data[C]//IEEE Radar Conference.[S.l.]:IEEE Press,2012.
[2] 付丽华,李宏伟,张 猛.基于小波变换的复杂噪声背景中谐波恢复方法[J].工程地球物理学报,2005,2(1):22-28.Fu Lihua,Li Hongwei,Zhang Meng.Method of harmonic retrieval in the complex noise based on wavelet transform[J].Chinese Journal of Engineering Geophysics,2005,2(1):22-28.
[3] Smith L I.A tutorial on principal components analysis[R].USA:Cornell University,2002.
[4] Chen V C.The micro-D effect in radar[M].Boston:Artech House,2011.
[5] 陈 凤,刘宏伟,杜 兰,等.基于特征谱散布特征的低分辨雷达目标分类方法[J].中国科学:信息科学,2010(4):624-636.Chen Feng,Liu Hongwei,Du Lan,et al.Classification method of low resolution radar target feature based on the characteristic of spectrum spread[J].Scientia Sinica:Information,2010(4):624-636.
[6] Petersson H,Bjorklund S,Karlsson M,et al.Towards surveillance using micro-Doppler radar[R].IRS(International Radar Symposium),2009.
[7] 陈行勇,黎 湘,郭桂蓉,等.基于旋翼微动雷达特征的空中目标识别[R].系统工程与电子技术,2006,28(3):372-375.Chen Xingyong,Li Xiang,Guo Guirong.Air target identification radar based on the characteristics of the rotor[R].Systems Engineering and Electronics,2006,28(3):372-375.
[8] Chen V C,Li F Y,Ho S S.Micro-Doppler effect in radarphenomenon,model and simulation study[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):2-21.

