基于蒙特卡罗模拟方法的项目工程造价风险分析

［摘要］本文主要通过蒙特卡罗模拟方法来定量进行工程造价风险分析并预测风险性造价。按照蒙特卡罗的原理，结合工程造价管理的方法给出造价风险模拟的关键步骤，最后以一个项目实例进行验证该方法的可行性。

［关键词］蒙特卡罗模拟；工程造价；风险分析

［中图分类号］TU723［文献标识码］A［文章编号］1005-6432（2013）2-0035-02

1引言

目前我国工程项目造价估算方法依然是根据设计文件以及定额或经验数据，计算出一个总的确定的数值，工程承包企业便以此定值为依据投标报价并制订成本计划。但实际上，工程项目在实施过程中往往受到诸如自然、劳动生产率、施工管理水平、市场等众多不确定因素的影响，各工序的成本具有较大的不确定性，并非是能事先确知的定值，而是服从某种概率分布的一个随机变量，因此构成的工程项目总造价也是一个随机变量，而应用蒙特卡罗模拟技术可以预测工程项目的总造价并进行风险分析。

工程实施过程中遇到各种风险因素对不同分项工作的影响程度是不同的，且有些风险因素之间还存在关联，难以用数学方法准确表示它们各自对工程造价成本的影响，但在各种因素的共同作用下，对工程某分项工作的总体综合影响是可知的，在工程施工时，在各种随机因素的共同作用下，各分项工程的成本值在某一范围内变化，而某分项工程的单位成本分布于一个区间内，有最大、最小值，在此区间内的分布也不均匀，存在一个最可能值，并且在进行大量的施工实践（模拟）后，它们会呈现出一定的规律性，服从某种统计规律，虽然不能确切地知道该值，但可以用数学方法对它们的分布情况加以描述，因此，可以依据工程项目的历史成本资料，考虑时间因素，计算出各分项工程的分布参数；可用蒙特卡罗法逐步模拟出拟建工程的可能成本区间以及实现某一计划成本值的可能性，以便为施工企业下一步风险决策、控制提供科学的理论依据。

2蒙特卡罗原理

蒙特卡罗（Monte Carlo）方法亦称为随机模拟（Random simulation）方法，有时也称为随机抽样（Random sampling）技术。该方法的基本思想是：首先建立一个概率模型或随机过程，使它的参数等于问题的解，然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，随后得出所求解的近似值。解的精确度可用估计值的标准误差来表示。

蒙特卡罗模拟法用于工程造价风险分析的实施步骤如下：

（1）分析哪些原始指标属于随机变量，并确定出这些随机变量的某些特征（如概率分布、均值、方差等）；

（2）通过模拟试验随机选取各随机变量的值，并使选取的随机值符合各自的概率分布。通常先产生均匀分布的随机数，然后生成服从某一分布的随机数据，方可进行随机模拟试验；

（3）建立经济评价指标的数学模型；

（4）根据模拟试验结果，计算出经济评价指标的一系列样本值；

（5）经过多次计算机模拟试验，求出经济评价指标的概率分布或其他特征值；

（6）检验试验次数是否满足预定的精度要求。

3造价风险模拟步骤

3.1预测模型的建立

根据工程造价投资费用的构成原理，采用WBS工程分解，把工程投资费用分解为以下内容：工程费用、工程建设其他费用、预备费、建设期利息和固定资产投资方向调节税（现暂停征收）。其中每一部分又包括很多详细的内容，把这主要的五部分汇总起来，就是工程造价投资费用，所以，

工程造价=（工程费用+工程建设其他费用+预备费+建设期利息）

3.2工程造价风险影响因素及其分布

选择合适的分布对Monte Carlo仿真来说非常重要，实际工作中，很难求得绝对反映客观实际的概率分布，即使是根据过去大量的统计资料或实验数据计算出来的数字，也总是有限的、相对的，不可能包括反映的全部事实。作为计算依据的资料也总是过去的资料，而时间、环境、条件和市场等因素时时刻刻都在发生变化，过去的资料并不能完全反映现在和将来，只能作为过去的演化规律用以判定未来；另外，在项目风险分析工作实践中，人们遇到的各种风险因素是不可能重复的，所以不可能做出准确的分析，更难以计算出风险发生的客观概率，也无法确定出风险对造价的影响大小。所以，我们可以发挥主观能动性，由风险管理的决策者及相关领域的专家对某些风险因素出现的概率进行主观估计，可以采取德尔菲法和专家经验判断法来估计分布概率，这是一种用较少信息量做出主观估计的方法。

3.3模拟次数的确定和随机数的产生

模拟的重复次数影响着结果的质量，一般重复次数越多，对输出分布的特性刻画及参数估计就越精确。在RiskSimulator软件中要求输入需要仿真试验的次数。进行3000次试验意味着会产生基于输入假设的3000个不同的结果。可以根据需要改变试验次数，但是键入的数值必须是正整数，系统默认的运行次数是1000次。同时可以利用精度和误差控制来自动帮助决定需要进行仿真的次数。

精度控制会自动确定所需的试验次数，当达到预先设定的精度水平时仿真就会停止。精度控制功能允许您自己设置想要的精度。一般来说，试验的次数越多，置信区间就越窄，统计数据也越精确。RiskSimulator里的精度控制功能利用置信区间的特征来确定是否达到了某统计量的精度水平。该软件会自动产生所需要的随机数。

4基于蒙特卡罗模拟方法的项目工程造价风险分析4.1项目概况

该工程为××综合楼工程，该建筑由连体建筑公用的地下部分、裙房部分和主体楼座及分摊的室外工程组成，费用包含工程费用，建设其他费用及预备费，项目建筑规模为41200M2，总投资为19223.59万元，包括：

工程费用16160.42万元，包括：

（1）主体建筑、装修工程，给排水工程，消防工程，采暖通风及空调，天然气工程，强电工程，弱电工程，车辆管理系统和电梯工程和室外工程等10个工程。

（2）工程建设其他费用为1585.32万元，包括建设单位管理费、城市基础社会配套费、环境影响评价费、地震安全评估费、交通评估费、伐移树木补偿费等建设前期费用、勘察设计费、施工图审查费、招标代理服务费、竣工图编制费、工程监理费和工程保险费等。

（3）预备费1064.74万元。

（4）建设期利息413.1万元。

其中通过软件提供的飓风图分析出建筑工程费用、工程建设其他费用、混凝土结构工程和玻璃幕墙是构成工程总投资的主要部分，也是工程造价计量产生风险的主要部分。

4.2工程费用模拟分析步骤

（1）按项目建立工程费用的电子表格模型，选择成本控制要素。在工程费用模拟模型构建过程中，我们采用从下到上的构建过程，即从最基本的成本构成要素逐级向上构建。案例中选取5个大项共计40个子项作为成本控制要素建立电子表格，主要包括：土建、装修工程费用，地下结构工程、混凝土结构工程、采暖通风空调系统、工程内建设其他费用和玻璃幕墙，预备费，裙房装饰等。

（2）规定关于变量概率分布的假设，RiskSimulator软件已准备好概率分布可供选择。案例中根据历史数据统计、经验值判断等方法，分别对各子项进行概率变量分布假设，选取正态分布、三角分布、均匀分布等作为各子项的分布假设（均由计算机自动完成）。本文根据实际情况，本着简化的原则，选择三角分布。

（3）规定预测单元即有关输出变量。案例中设定“工程造价”。

（4）设定迭代次数。一般而言，迭代次数越多，模拟结果越精确。案例设定迭代次数为3000次，该数据在下图中显示。

（5）运行模拟。在“运行首选”对话框内选择定义蒙特卡罗模拟，然后运行模拟。

（6）模拟结束后，在图中定义置信水平（案例中定义置信度为95%），从而测算出造价范围。

4.3工程费用模拟运行结果分析

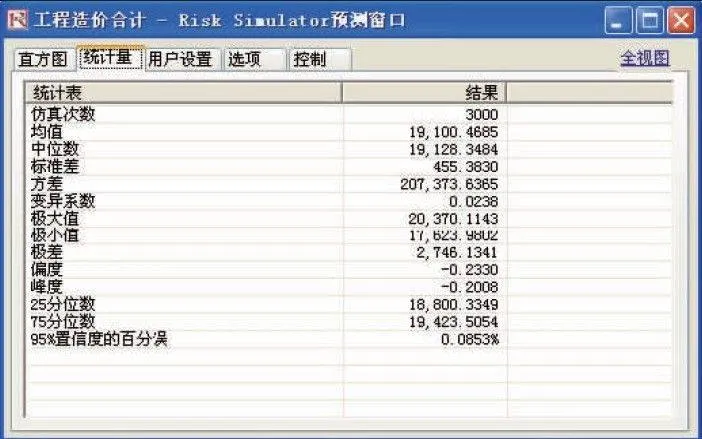
对工程造价预测参数图进行分析，可得到工程造价均值为19100.4685万元，中值19128.3484万元，标准差为455.3830万元等统计参数。

由下图可见，项目总造价经过3000次迭代后极大值为20370.1143万元和极小值在17623.1341万元范围内波动，变动跨度在2747万元左右，在置信水平不同时，工程造价的取值范围也不尽相同。

而我们通过静态估算方法估计投资费用为19223.59万元，相当于其置信水平为80%的投资估算。

工程造价预测参数图

5结论

通过以上分析可以看出，利用蒙特卡罗模拟可以考虑各种不确定性因素对工程造价的影响，对工程造价结果进行风险性分析，为工程投资决策和报价决策提供依据，现有的预算软件只需修改参数的输入，并增加一个随机数产生的模块，即可实现该功能。但这种方法要求建立在对以往资料的统计分析比较详细、对未来变化的估计比较可观的基础上，才能得出较为合理有效的数据。

参考文献：

［1］王中伟.用EXCEL实现工程项目的蒙特卡罗模拟分析［J］.广东交通职业技术学院学报，2005（1）：101-103.

［2］石劲松.基于工程量清单报价方式的工程造价改革［J］.时代经贸，2007（1）：101-103.

［3］王军武，张声东，张露.试论蒙特卡罗风险分析中的变量相关性问题［J］.国外建材科技，2004（3）：84-86.