空间通信远距离非均匀天线组阵技术研究

高超垒 宋振宇 战勇杰

（北京卫星信息工程研究所，北京 100086）

1 引言

随着距离地球越来越远，深空探测器到达地面的信号变得越来越弱，需要一种能补偿信噪比（SNR）降低的方法。最大天线口径和最低接收机噪声温度已到极限，有效提高SNR 的唯一方法就是对来自几副天线的信号进行合成，称为组阵。天线组阵的优点是：能比单副天线以更高数据速率接收数据。在“旅行者”（Voyager）探测器与海王星相遇期间，超大阵（VLA）射电望远镜（位于新墨西哥州）和戈尔德斯顿（位于加利福尼亚州）的天线之间用符号流合成（SSC）进行符号组阵处理，就是一个例子［1-2］。这一技术提高了数据传输速率，增加了从探测器返回的科学数据量。

目前，天线组阵技术多用于窄带低速率的遥测信号接收，可用于任何信号调制格式，如二相相移键控（BPSK）、四相相移键控（QPSK）、连续相位调制（CPM）等。天线组阵技术中常用的信号合成方法有5种，即全频谱合成（FSC）、复符号合成（CSC）、SSC、基带合成（BC）和载波组阵（CA）。针对非均匀天线组阵技术的研究，文献［3］在SUMPLE 算法的基础上提出了一种适用于非均匀阵的相位补偿和信号强度估计方法；但这种方法仅适用于近距离天线组阵、信号速率较低、SNR 较高的情况，且计算量较大。本文以2副远距离接收天线为例，提出了一种远距离非均匀天线阵信号的合成方法，将天线组阵技术推广到了远距离非均匀阵和高数据速率的情况。因为天线分布在不同的地区，并且天线口径、G／T值等指标均不相同，所以考虑采用SSC方法对信号进行合成。在此基础上，引入快速傅里叶变换（FFT）方法实现信号时差的自适应估计和消除，可比传统的时差估计算法扩大时差的估计范围；采用最小均方（LMS）误差算法实现信号的自适应最大比合成（MRC），无须估计信号的SNR，可用于遥感卫星较高数据速率信号的接收。因此，本文采用的方法可提高接收信号的可靠性，提高数据速率，增加链路余量，降低接收信号SNR 门限等。

2 远距离非均匀天线阵信号的合成算法

2．1 常用的信号合成算法

在深空通信中，常用的信号合成算法有SIMPLE算法和SUMPLE算法。SIMPLE算法（见图1）中，指定多副天线中的一副作为参考天线（通常是G／T值最大的天线）。参考天线作为阵的相位中心，来自其余天线的信号与来自参考天线的信号相关，用这个相关结果修正其余天线的信号，使它们在相位和时间延迟上与参考天线的信号一致，最后将所产生的信号相加，提高SNR。提高的程度取决于修正后信号在相位上对齐的程度，修正相位精度的极限，由获得相关结果所用的平均时间确定。如上所述，该平均时间很大程度上受限于天线信号穿过对流层时引起的相位变化。

图1 SIMPLE算法原理Fig．1 Schematic of SIMPLE algorithm

SUMPLE算法［3-4］（见图2）可以描述为，每副天线的信号与由其他所有天线信号的加权和组成的参考信号互相关。这是一种迭代方法，与SIMPLE算法相比，可应用于更弱的信号，所需处理也更复杂，但仍与天线数量成正比。与SIMPLE 算法不同，SUMPLE算法中各天线的信号并没有与某一个参考信号对齐，而是与一个流转参考信号对齐。仿真结果表明，这种参考的相位漂移在低SNR时较大。

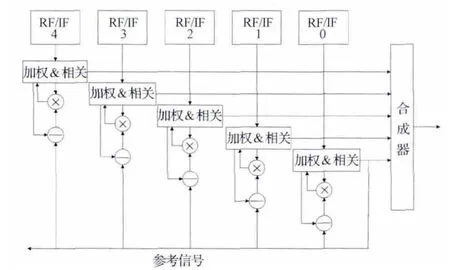
图2 SUMPLE算法原理Fig．2 Schematic of SUMPLE algorithm

2．2 本文采用的信号合成方法

上述两种算法的适用范围是近距离组阵在射频段对信号进行合成，即航天器信号到达各副天线的相对时延的变化范围小，可事先估计和计算出来并被消除；因此，只要考虑各信号之间的相位漂移，SIMPLE和SUMPLE算法都能表现出不错的应用效果，但是并不适用于远距离地面站之间的天线组阵。由于天线距离很远，并且不同地区的天线指标不同，要获得最大的SNR 输出，就要对不同信号的加权值进行估计和计算；同时，要能接收较高数据速率的信号，保证接收信号的可靠性，且接收信号的门限也比较高，根据经验可知，载波跟踪的门限大约在-3dB，因此，本文考虑采用SSC 方法对信号进行合成。

SSC［5］是实符号组阵，如图3 所示。其优点是可以忽略合成损失，且能以数据速率带宽实施。分布在各地区的天线，可以实时或非实时地将其符号发送至中心站，在那里符号流合成器输出最终的符号。不过，这要求每副天线都能锁定在各自的信号上，并且要使用多个载波跟踪装置、副载波同步装置和符号同步装置，对于较高的调制指数，在每副天线使用边带辅助，可减小载波恶化。

图3 符号流合成原理Fig．3 Schematic of SSC

为获得较好的合成效果，在SSC 方法中引入时差估计和最大SNR 合成算法，实现远距离天线阵信号合成，同时能接收较高数据速率的航天器信号，合成方法如图4 所示。其中：时差估计和消除采用FFT 方法，实现信号互相关［6-9］；信号合成采用LMS方法，实现最大SNR 合成［10-12］。

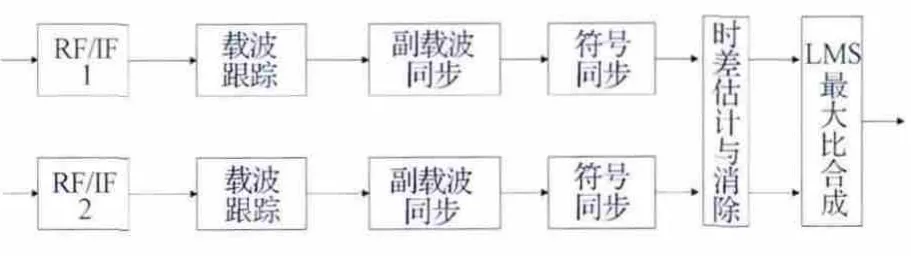
图4 远距离天线组阵方法原理Fig．4 Schematic of long-distance antenna arraying

2．3 信号时差估计和消除的实现方法

目前，时差估计方法主要有互相关法、自适应滤波法和基于高阶统计量法。互相关法是通过信号的互相关函数滞后的峰值，估计信号之间延迟的时间差，方法简单，容易实现，但要求信号和噪声、噪声和噪声互不相关，广义互相关法还需要信号与噪声的先验知识，且只能估计整数倍时差值。文献［7］提出的自适应滤波法，不必获得信号和噪声的统计先验知识，通过调整自身参数，可以跟踪时变的时差，但当滤波器阶数较高时，存在计算量大、收敛速度慢等缺点。基于高阶统计量法是利用高阶统计量处理接收信号，有效抑制高斯和非高斯有色噪声的影响，从而提高SNR，在相关噪声条件下，具有较好的时差估计性能，但该方法需要更长的数据长度和更大的计算量。

在本文的方法中，采用FFT 方法来实现互相关，将时差的估计转换到数字域，增大相关长度（即可扩大时差估计范围）。2路数据的时延误差，采用数据间的自相关特性得到，即当2路数据完全对齐时，其相关计算得到的结果最大，否则，其相关计算得到的结果较小。由于时域信号的卷积运算等效频域的乘法运算，因此，时差检测原理可由图5表示。

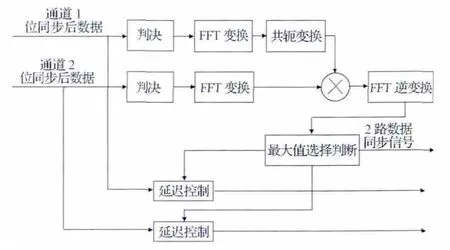
图5 时差检测原理Fig．5 Schematic of time-delay error detection

2个通道位同步后数据经判决，通过FFT 变换转换到频域。通道1的频域数据进行共轭变换后与通道2的频域数据进行相乘，相乘结果再通过FFT逆变换转换到时域。通过这样的转化处理，实现了2路数据的相关运算，简化了处理流程。完成相关运算的数据，通过最大值选择判断模块得到2路数据的时差，分别控制2路延迟控制模块，实现2路数据的时差消除。

2．4 信号最大SNR 合成实现方法

信号合成的常用方法有选择式合并、等增益合并和MRC 方法。选择式合并通常用于抗多径衰落，即从多路信号中选择出SNR 最大的那路信号，合成增益就是SNR 最大的那路信号。其优点是实现方法简单；缺点是不能有效地利用低SNR 的信号，无法进一步提高合成增益。等增益合并是将每路信号等权值相加，从而获得合成信号，合成增益与每路信号的SNR 都有关系。其优点是合成方法简单，在2路信号SNR 相差不大时，可以获得较好的合成增益；缺点是不能达到最优的合成增益。MRC是根据每路信号的SNR 给出对应的合成权值，从而使合成信号获得最大的SNR。

传统的合成方法要事先估计出信号的SNR，因此，运算量大，结构较复杂。本文采用LMS算法实现信号的MRC，而不必估计SNR。LMS算法基于恢复信号与期望信号均方差最小的原理［9］，实现系统自适应的收敛。以2 路信号合成为例，假设第1路信号的比特信噪比（Eb／N0）为E1，第2路 的Eb／N0为E2，合成信号Eb／N0的理论增益为ET，则

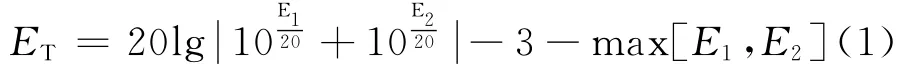
将2路信号的噪声功率归一化，可得2路信号的理论合成增益为式（1），其合成权值的比值为10（E1-E2）／10。自适应的LMS算法实现信号MRC 的原理如图6所示。

设向量S（m）＝（s1（m），s2（m）），λ（m）＝（λ1（m），λ2（m）），合成后的信号r′（m）＝λ（m）S（m），误差信号ε（m）＝r（m）-r′（m），则均方误差可表示为

式中：RrdT＝E［r（m）ST（m）］；Rrr＝E［S（m）ST（m）］。由以上推导可知，对λ（m）的求解，要精确知道RrdT和Rrr的先验统计，并且还要进行矩阵的求逆运算，这对系统的实现造成很大的困难。因此，工程中采用基于最速下降法推导出来的Widrow-Hoff LMS近似算法，其λ（m）的递推公式为

式中：μ为控制收敛速度与稳定性的常数，称为收敛因子，在实际工程应用中可以通过测试得到。

图6 LMS算法原理Fig．6 Schematic of LMS algorithm

3 仿真验证

本文考虑2路信号合成，将存在时差的2路信号经过内插环路后合成进行仿真，采样率为1200MHz，载波频率为720 MHz，信号调制方式采用QPSK，数据速 率 为300 Mbit／s，采 样 点 数 为1 000 000 个。在此条件下，对比特信噪比Eb／N0为-3～0dB时进行仿真。

3．1 互相关求时差效果仿真

由于2路信号位同步后的数据SNR 较低，存在较多误码，因此2路信号相关的点数直接影响相关峰的高低。在本文的实现方法中，时差估计范围等效于进行FFT 运算的点数。按照SNR 为-3dB，2路信号时差为100bit进行仿真分析，采用256点、512点、1024点FFT 运算，在纯随机数据条件下，得到的相关峰（幅度值）结果如图7所示。其中：横坐标轴表示相关峰的位置，纵坐标轴表示相关峰的峰值（只是一个量值，无实际物理单位）。

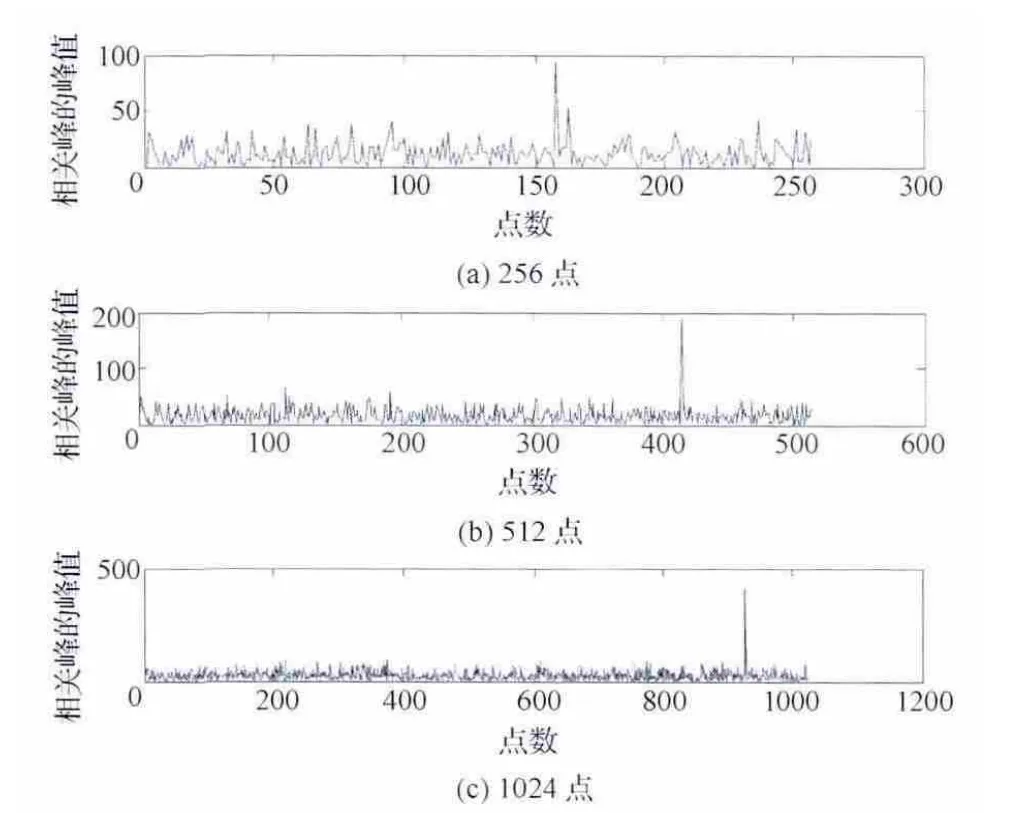
图7 互相关运算仿真结果Fig．7 Simulation results of cross-correlation operation

从图7可以看出：当SNR 较低且2路信号时差较大时，采用256点相关运算得到的相关峰的峰值已经很不明显，对信号延迟的准确判决会造成很大的影响；当把相关点数提升到512点和1024点时，2路信号相关峰的峰值已经比较明显了，可以比较准确地判决出2路信号延迟。

3．2 LMS算法实现信号合成仿真

设定s1（m）的比特信噪比为-3dB／Hz，s2（m）的比特信噪比为0dB／Hz，可得2路信号的合成加权值之比λ1（m）／λ2（m）应为0．501。在同样比特信噪比条件下，设置λ1（0）＝λ2（0）＝1，利用LMS算法获得的仿真结果如图8所示。从图8可以看出，最终2路信号在收敛以后λ1（m）／λ2（m）的均值为0．500 5。根据这一仿真结果，计算可得方差为0．021，满足最大SNR的合成要求，合成增益与理论增益之差小于0．25dB。

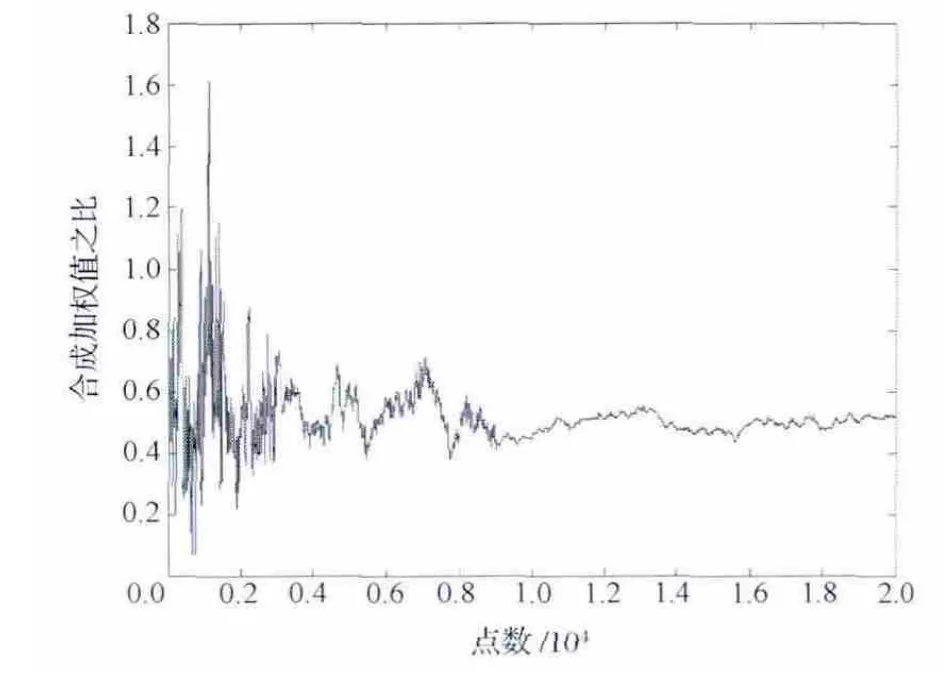
图8 LMS算法仿真结果Fig．8 Simulation results of LMS algorithm

4 结论

本文采用一种可用于接收较高数据速率航天器信号的远距离非均匀天线组阵方法，将天线组阵技术应用在遥测信号的接收领域，并推广应用到遥感卫星等较高数据速率的空间信号接收，得出如下结论。

（1）在远距离非均匀天线组阵时，SSC 方法更合适。

（2）在远距离非均匀天线组阵时，引入信号时差估计，可以自适应地消除信号时延，互相关长度决定时差消除范围。

（3）利用LMS算法对信号进行最大SNR 合成，无需SNR 估计，具有较快的收敛速度，且可以达到与理论值接近的效果。

（References）

［1］Gatti M S．The deep space network large array，AIAA 2003-6418［R］．Washington D．C．：AIAA：2004

［2］李海涛，丁溯泉，董光亮，等．天线组阵技术研究及其在我国深空测控通信系统中的应用［J］．飞行器测控学报，2008，27（3）：10-14

Li Haitao，Ding Suquan，Dong Guangliang，et al．Researches on antenna arraying technology and its applications to deep space TT＆C system［J］．Journal of Spacecraft TT＆C Technology，2008，27（3）：10-14（in Chinese）

［3］孔德庆，施浒立．非均匀天线组阵SUMPLE权值信噪比及信号合成性能分析［J］．宇航学报，2009，30（5）：1941-1946

Kong Deqing，Shi Huli．Study of weights performance and combining loss of SUMPLE algorithm for non-uniform antenna arraying［J］．Journal of Astronautics，2009，30（5）：1941-1946（in Chinese）

［4］Rogstad D H．The SUMPLE algorithm for aligning arrays of receiving radio antennas：coherence achieved with less hardware and lower combining loss，the Interplanetary（IPN）Progress Report 42-162［R］．Pasadena，California：Jet Propulsion Laboratory，2005

［5］Hurd W，Rabkin J，Russell M D，et al．Antenna arraying of voyager telemetry signals by symbol stream combining，the Telecommunications and Data Acquisition（TDA）Progress Report 42-86［R］．Pasadena，California：Jet Propulsion Laboratory，1986

［6］罗进文，胡正伟，蒋占军，等．窄带音频信号时差估计算法［J］．计算机应用，2011，31（3）：636-638

Luo Jinwen，Hu Zhengwei，Jiang Zhanjun．Time delay estimation algorithm for narrowband audio frequency signal［J］．Journal of Computer Applications，2011，31（3）：636-638（in Chinese）

［7］Widrow B，Steam S D．Adaptive signal processing［M］．Englewood Cliffs：Prentice-Hall．Inc．，1993

［8］Gardner W A，Chen C K．Signal-selective time-difference-of-arrival estimation for passive location of manmade signal sources in highly corruptive environments，part I：theory and method［J］．IEEE Trans on Signal Processing，1992，40（5）：1168-1184

［9］Gardner W A，Chen C K．Signal-selective time-difference-of-arrival estimation for passive location of manmade signal sources in highly corruptive environments，part II：algorithms and performance［J］．IEEE Trans on Signal Processing，1992，40（5）：1185-1197

［10］Loskot P，Beaulieu N C．Maximum ratio combining with arbitrary correlated generalized Ricean branches［C］／／Proceedings of the 2004 Wireless Communications and Networking Conference（WCNC）．New York：IEEE，2004：333-338

［11］Cui J，Sheikh A U H．Outage probability of cellular radio systems using MRC in presence of multiple interferes［J］．IEEE Trans on Communications，1999，47（8）：1121-1124

［12］Mayyas K．Performance analysis of the deficient length LMS adaptive algorithm ［J］．IEEE Trans on Signal Processing，2005，53（8）：2727-2734