程序设计与数据结构课程的融合教学模式研究

冯莹莹 周红志

(阜阳师范学院信息工程学院，安徽阜阳 236041)

在高等院校所开设的计算机专业课中，程序设计和数据结构都是重要的专业基础课和核心课程。程序设计重视语法，忽略了对学生编程能力的培养;数据结构的体系相对来说较抽象，脱离了基础知识的依托，增加了课程的理解难度。通过分析两门课程之间的衔接性，对程序设计和数据结构的内容进行有效整合，调整两门课程的知识体系结构，改革教学方法，使教学效果更好。

1 融合教学模式

融合教学模式是一种新的计算机专业学科相互交叉、相互整合的教学模式。在对程序设计与数据结构的教学改革中，采用以数据结构为核心和主线，融合程序设计的相关知识，注重内容的衔接性和前沿性，坚持理论联系实践的教学模式，优化了知识的学习和融合，提高了学生的编程能力，从而实现了最优的教学效果。

2 目前教学中存在的问题及教学改革背景

传统的教学过程中，人为的隔断了程序设计与数据结构两者之间的联系，导致内容脱节，学生不能真正的把语言知识应用到数据结构编程中去，主要存在以下问题:

(1)数据结构的教学内容抽象，复杂，算法实现仅仅是描述而已，使学生的算法设计实践能力受到影响。

(2)前导课程C程序设计主要注重语法知识的讲解，而且没有把结构体这一章作为重点，而数据结构又与结构体息息相关，导致学生在编程中不能将结构体相关知识点灵活运用。

(3)教学方法仍然以传授为主，无法提高学生学习相关课程的积极性。

为了更好的培养和提高学生分析问题，解决问题的能力，有必要分析数据结构与程序设计跟其他相关课程之间的前导后续关系(图1)。围绕课程的教学目的，在教学内容的实施过程中，实现了数据结构与程序设计跟相关其他课程间的有效整合。整合过程中，指出相关计算机专业课的衔接知识点，在此基础上形成一条完整的课程学习链，避免相关课程脱节。图1中单箭头表示前导关系，双箭头表示课程相关。

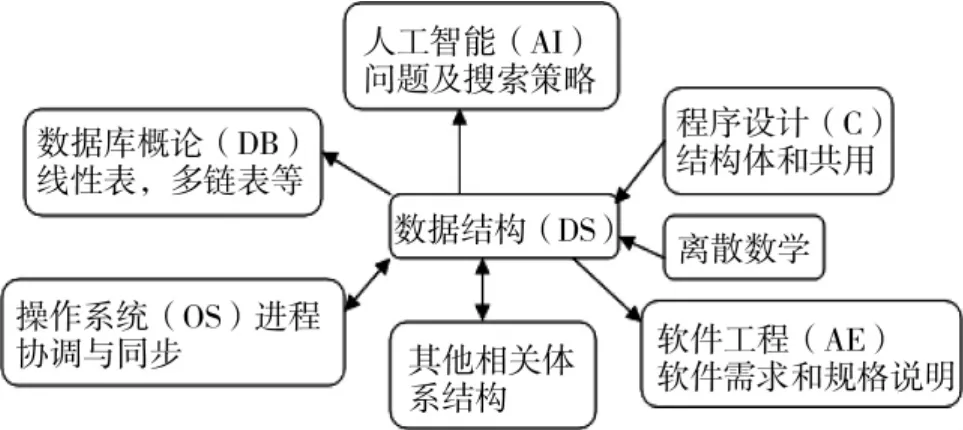
图1 程序设计与数据结构的前导后续课程的关系

3 融合教学设计思路

鉴于数据结构与程序设计两门课程的内容特点，构建了基于任务驱动的案例法双线教学理念。第一条是一条显式的主线，主要是对数据结构和程序设计基本知识由浅入深，自顶向下的学习和吸收。在讲授数据结构中的线性表，队列，栈，二叉树及图等内容时，首先寻找它们之间的共性，都需要用ADT表示每一类数据结构，其次对于每一种数据结构的具体应用都可以用C程序设计实现。第二条主线就是应用各种数据结构解决现实生活问题能力的培养，通过对数据结构中实例及经典问题的剖析，采用归纳式学习法，分派具体任务进行课程单元设计，促进编程能力的提高。两条教学主线相辅相成，最终实现知识的灵活运用。

4 程序设计与数据结构融合教学实践

探索将两门课程有效整合的方法。下面以单元设计为例简要介绍课改的实施(以C程序设计语言进行分析)。

单元设计采用基于任务驱动的案例法教学模式。数据结构的知识非常灵活和抽象，要求具备较强的逻辑思维能力，在教学过程中可以给出生活中的实例进行讲解，帮助学生把课本上的理论知识跟实例联系在一起，使抽象深奥的知识更加生动有趣。比如在讲数据结构中栈的知识时，可以以表达式求值为例来说明栈的先进后出特点，并对表达式中各运算符的优先级加以分析。在讲图的最短路径算法时，可以结合现实生活中交通旅游的线路选择问题。单元设计是培养学生综合运用所学知识，分析问题、解决问题，锻炼实践能力的重要环节，该环节直接决定了教学效果的好坏。

下面以图的最短路径算法为例介绍基于任务驱动的案例法的实施过程。问题情境来源于课程，启发学生“如何求解最短路径”，教师介绍图的数据结构和图的最短路径基本算法，结合实际例子引导学生自主完成课程设计。图2为单元设计实施图。

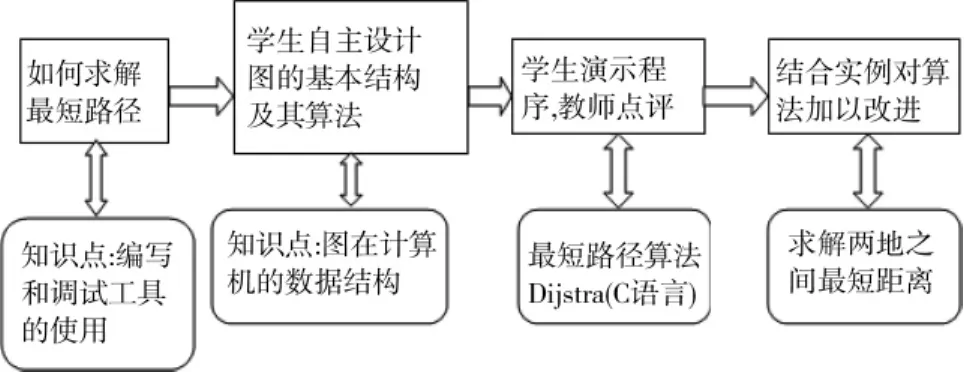
图2 单元设计实施图

采用图2中相关知识求解最短路径，可转为求解两地之间最短距离，最低开销或最少时间等。本设计中包含建立图的数据结构，单源点最短路径算法实现。

(1)建立图的数据结构

图中顶点之间的关系用邻接矩阵来表示。设G=(V，E)为具有n个顶点的带权图，其邻接矩阵为具有以下性质的n阶方阵:

(2)Dijkstra算法求解单源点最短路径

按照从源点到其余每一个顶点的最短路径长度的递增顺序依次求出从源点到其他各顶点的最短路径及长度，每次求出从源点vi到一个终点vj的最短路径及长度后，都要以vj作为新考虑的中间点，用vi到vj的最短路径和最短路径长度对vi到其他尚未最后求出最短路径的那些终点的当前最短路径及长度作必要的修改，使之成为当前新的最短路径和最短路径长度，当进行n-2次后算法结束。

具体步骤如下:

(I)初始时，S只包括顶点v，即S={v}，V-S包括了除v以外的其他所有顶点，v的距离为0，V-S中的顶点的距离值这样确定:对V-S中的任意顶点u，若图中有边＜v，u＞，则u的距离为此边上的权值，否则u的距离为∞(或用一个很大的数表示，在下面的程序中以maxint表示)。

(II)从V-S中选一个距离最小的顶点k加入到S中，此时k的距离值恰好就是从v到它的最短路径的长度。

(III)S中加入一个顶点k后，对V-S中的各个顶点的距离进行一次修正。对V-S中的任意顶点u，若k的距离值加上边＜k，u＞上的权值小于u的原距离值，则将u的距离值调整为k的距离值与边＜k，u＞上的权值之和，否则u的距离值保持不变。

(IV)重复步骤(II)和(III)，直到所有顶点都已包括在S中为止，即直到S=V为止。

下面以简化抽象交通网络图为例说明单源点最短路径算法的实现。

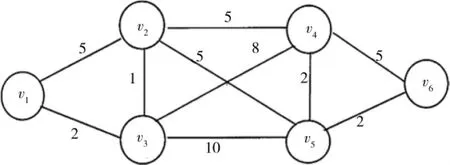
图3 交通网络图

图3是一个包含有6个城市的交通网络图，两顶点之间的边权表示两城市之间的长度，求从v1到v6哪条路径费用最低。通过分析得知求得两顶点之间的最短距离即可求解。作出图3的邻接矩阵:

逆向求得最短路径路线走向:v1-＞v3-＞v2-＞v4-＞v5-＞v6，v1到v6两城市之间的最短距离为12。

为了加深学生对相关算法的理解，课题组还精心设计了数据结构典型算法的flash动画。比如二叉排序树的生成、建立，图的深度优先遍历、广度优先遍历，单链表结点的插入、删除以及各种排序方法的动画演示。

5 教学改革的效果

(1)教改使学生的学习主动性有了极大提高。利用数据结构的知识解决有趣的现实问题，在很大程度上激发了学生学习的主动性。如利用赫夫曼书进行密码编排和密码解密问题，利用最短路径求解交通旅游的线路选择问题等。

(2)理论与实践并重，使学生熟练掌握理论知识，拓展知识面。将同一个问题设计和贯穿在不同的教学理论和实践单元中，如排序问题既可以用链表解决，也可以用数组解决，约瑟夫问题既可以用循环链表求解，也可以用环形队列求解。利用这种教学方式，既巩固了学生的理论知识，又拓展了知识面，锻炼了学生的动手实践能力，真正达到通过实践教学深化理论教学的目的。

［1］张红霞，盘丽丽.《数据结构》课程教学改革研究与探讨［J］.现代计算机(专业版)，2009(6):79-81.

［2］周玉林，赖鑫生.《数据结构》教改中的问题研究与探讨［J］.上饶师范学院学报，2008(3):84-88.

［3］张娟，安少华，胡选子，等.《数据结构》课程的教学改革与实践［J］.计算机教育，2008(16):53-54.

［4］沈奇.计算机科学与技术专业应用型本科师资队伍建设探析［J］.计算机教育，2010(16):65-67.

［5］ZHAN F B.Three Fastest Shortest Path Algorithms on Real Road Net-works［J］.Journal of Geographic Information and Decision Analysis，1997，1(1):69-82.

［6］严蔚敏，吴伟民.数据结构［M］.北京:清华大学出版社，1997.