再入飞行器多约束预测－修正末导引律研究

冯必鸣，聂万胜，李 柯

（装备学院 航天装备系，北京101416）

无动力面对称滑翔飞行器的投弹倾角和速度将极大地影响末制导弹药的攻击性能，尤其是某些精确末制导弹药对最大命中速度存在限制的情况下，更准确的投放速度和投放倾角就显得尤为重要，因而有必要对飞行器弹药投放阶段倾角和速度约束下的导引律开展研究。国内外就再入飞行器制导控制[1－5]、末端能量管理及精确打击武器终端倾角约束的末导引律开展了大量研究[6－11]。但是，再入制导和末端能量管理研究中普遍采用的标准轨道跟踪方法较难适应复杂多变的战场环境；精确打击武器制导律研究则在终端倾角约束方面做了大量工作，而对倾角和速度双重约束下的导引律研究甚少。文献[12－14]虽开展了速度控制研究，但都未能实现面对称滑翔飞行器末端速度和倾角的准确控制。因此，本文设计了一种在终端倾角及速度约束下的预测－修正导引律，以满足飞行器准确投弹的需要。

1 多约束预测－修正导引律设计

1.1 倾角约束下预测指令生成

本文在预测制导律设计时将飞行器相对运动分解到俯冲平面和转弯平面上[15]，坐标系建立以及飞行器俯冲平面与转弯平面的定义如图1所示。图中，γD（γD＜0），λD分别为速度在俯冲平面内的方位角、视线角；ηD为速度矢量与视线的夹角；R为相对距离为相对接近速度；λT为转弯平面内的方位角。

图1 相对运动坐标系

根据相对运动关系，可以得到关系式：

由式（1）～式（3）得俯冲平面内相对运动方程：

式中：av为线加速度。

弹道下压阶段末制导的目的是将飞行器引导至弹药投放位置（如图1所示O点），并保证飞行器具有期望的弹道倾角。因此，终端时刻视线角要等于期望的速度倾角，并且保证视线角速度为0，可以表示为

式中：tf为终端时间，γDf为终端期望方位角。

本文采用滑模变结构控制设计制导律，设滑模开关函数为[14]

式中：KD为滑模控制系数。

取俯冲平面内倾角约束下变结构导引预测控制律为

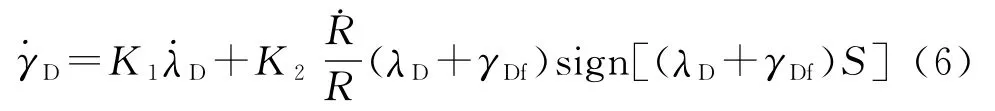
式中：K1，K2为导引律控制参数。

为了抑制高动态飞行引起的控制变量抖动[16]，采用S/（｜S｜＋δ）代替sign[（λD＋γDf）S]，得到俯冲平面内预测控制律为

式中：δ为一微小量，本文取为0.01。

转弯平面内的导引控制主要考虑修正机动减速引起的侧向距离偏差，该平面内的导引控制可采用如下形式的比例导引律生成预测控制指令[17]：

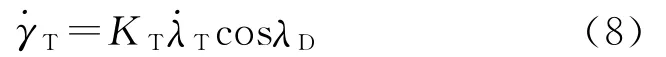
根据目标坐标系与视线坐标系之间的关系，可得2个坐标系之间的转换矩阵为

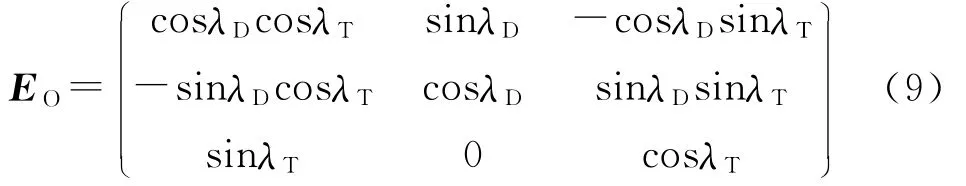
由此得到视线坐标系下各个速度分量的表达式：

式中：下标ξ，η，ζ分别表示沿视线方向、垂直于视线方向和视线侧向的分量。进而可以求得＝vη/R＝－vζ/（RcosλD）。

1.2 速度约束下修正指令生成

根据文献[15]所述，产生附加攻角是飞行器减速最简单易行的方式。根据末制导控制规律，可以确定飞行器速度方向的转率为

式中：m为飞行器质量，Cαy为升力系数，Δα为附加攻角[17]：

式中：CαN为总法向力系数。由此可得速度方向转率的增量为

式 中：速 度 限 制 条 件v＊＝vlimit，K＝（升力系数和总法向力系数可取一个范围内的平均值），因此本文设系数K＝6.5，修正系数Kl＝0.05。

图2 速度方向转率示意图

根据图2可以得到加入减速修正后俯冲平面和转弯平面内的控制律分别为

2 弹道仿真模型

2.1 飞行器动力学方程

本文假设飞行器飞行过程中依靠改变攻角α和倾斜角σ来实现飞行器的导引飞行[18]。因此，可得到简化后的飞行器三自由度动力学方程为[19]

式中：FD为阻力，FL为升力，θ为弹道倾角，ψ为弹道偏角，gh为重力加速度。

2.2 导引方程

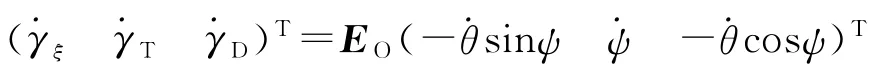
可分别得到弹道倾角和弹道偏角的预测控制律和修正控制律。

预测控制指令：

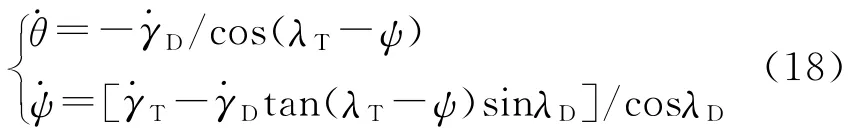
修正控制指令：

将式（18）和式（19）代入式（17）中，整理后可分别求得预测攻角αpre、预测倾斜角σpre和修正攻角αmod、修正倾斜角σmod。计算过程中控制量及过载约束为：－10°≤α≤30°，－60°≤σ≤60°，｜nx｜≤5g，｜ny｜≤5g，｜nz｜≤5g。计算中根据上述所示控制角和过载限制条件，最终确定可用的α和σ，获得气动力FL和FD，进而对式（17）采用四阶龙哥库塔积分求解末弹道。计算流程如图3所示，图中vter为预测得到的终端速度。

图3 预测修正仿真流程

3 仿真结果对比分析

本文假设飞行器弹药投放点高度分别为13km和3km，开展飞行器预测－修正末导引飞行仿真。飞行器质量m＝907.8 kg，气动参考面积为0.484m2，飞行器初始参数及终端要求如表1所示。计算过程中变结构控制参数KD＝6，K1＝－5，K2＝4，KT＝3，仿真过程中弹道预测时间步长为1s，导引飞行轨迹仿真时间步长为0.1s。表中，L为飞行器到目标点的距离；H0为飞行器初始高度；θ0为初始倾角，ψ0为初始偏角；Hf为飞行器终端高度；θf为终端倾角；vf为终端速度。

表1 飞行器初始参数及终端要求

图4所示为倾角－速度约束预测修正制导与倾角约束制导控制下飞行器的空间飞行轨迹，通过对比可以发现，采用机动减速修正控制后的再入飞行器具有明显的大侧向转弯机动，目标点位于高空时侧向机动距离Z最远接近6km，目标点位于低空时侧向机动距离Z也超过3km，利用这种侧向转弯机动方式不但可以达到减速的目的，而且飞行器还能够通过侧向机动飞行减小被地面防空火力拦截的概率。

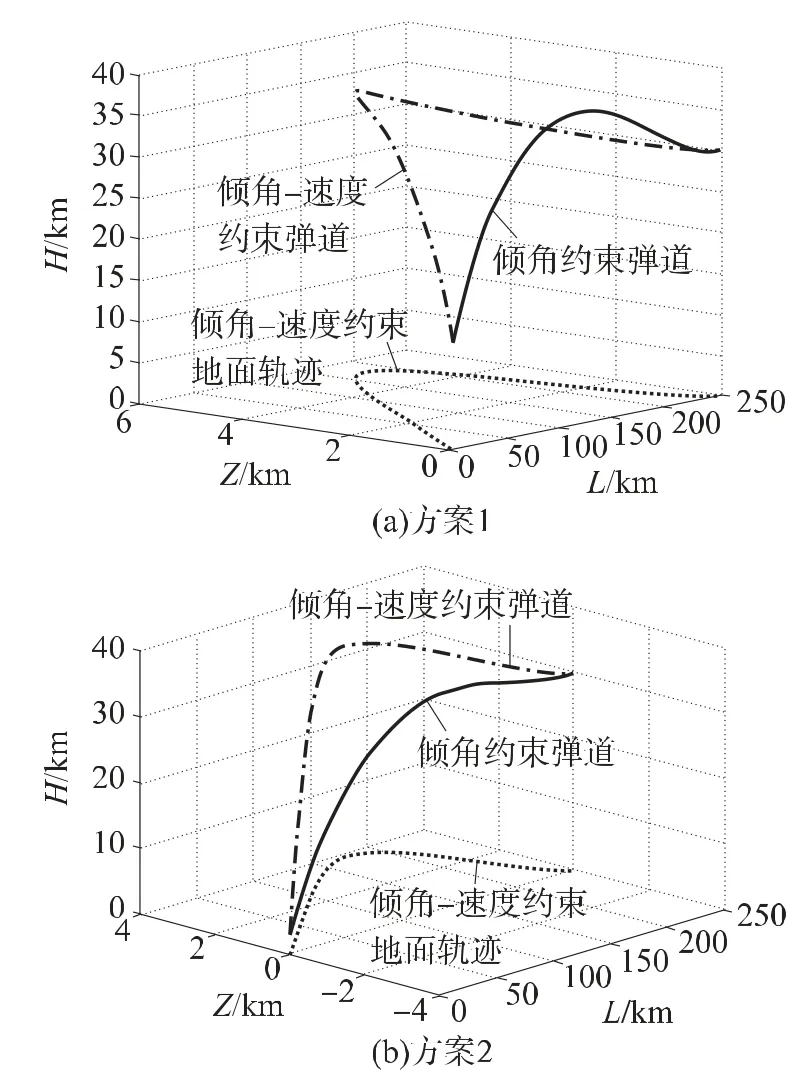
图4 空间弹道对

本文设计的预测－修正制导律旨在保证飞行器按照终端要求的倾角及速度达到指定弹药投放位置。从图5所示飞行器速度、倾角及偏角变化情况的对比中不难发现，无速度约束下的制导律仅在飞行俯冲平面内产生控制指令，弹道偏角始终保持180°，而本文设计的预测－修正制导律在机动减速要求下生成一定的倾斜角控制指令，实现飞行器的侧向机动飞行，也正是这样的侧向机动飞行，使飞行器终端速度降低到期望的水平。

从图5所示飞行器速度变化可以发现，采用单一的倾角约束制导律，飞行器在高低空达到的终端速度约为1 550m/s和1 450m/s，远高于期望的终端速度1 200m/s；而采用本文设计的制导律，飞行器在高低空达到的终端速度都接近1 200 m/s。这充分说明，本文设计的倾角－速度约束下的预测－修正制导律能够将飞行器终端速度很好地控制在期望范围以内，并且其终端倾角也满足期望值要求。

图5 飞行速度、弹道倾角及弹道偏角对比

对比分析图6所示攻角及倾斜角变化情况可以发现，采用本文设计的预测－修正导引律控制时，飞行器初始阶段采用大攻角维持飞行高度，并采用大倾斜角进行侧向机动，进而达到减速的目的。这一现象从图5所示速度变化也能看出，飞行初期飞行器速度下降较快；随后飞行器几乎保持0°倾斜角飞行，攻角也逐渐减小，整个飞行过程中攻角和倾斜角都没有剧烈波动，并且各向过载nx，ny，nz均在限制范围以内，如图7所示。

图6 攻角及倾斜角对比

图7 各向过载对比

4 结论

本文以末端期望速度为基准，采用倾角约束下的滑模变结构末制导指令进行弹道预测，并根据实际飞行速度与终端期望速度的偏差生成修正指令，进而形成倾侧角控制指令，采用侧向机动方式实现飞行速度的控制。仿真结果显示，采用本文设计的预测－修正制导律能够保证飞行器以期望的速度及倾角飞抵指定弹药投放位置，并且机动飞行弹道更有利于飞行器末端突防。分析飞行器控制参数变化发现，飞行器在整个制导飞行过程中，预测－修正导引律形成的飞行控制指令未出现大幅振动，且飞行器各向过载均在限制范围以内。

[1]AFZAL M I，ROESER H P，GRAESSLIM M.An explicit guidance method for a lifting interplanetary re－entry vehicle，AIAA 2009－6108[R].2009.

[2]LI Ping.Assessment of adaptive guidance for responsive launch vehicles and spacecraft， AFRL－RV－PS－TR－2009－1023[R].2009.

[3]ASHOK J，SIVAN K，SAVITHRI S A.Predictor－corrector entry guidance algorithm with path constraints for atmospheric entry vehicles[J].Journal of Guidance，Control，and Dynamics，2007，30（5）：1 307－1 318.

[4]McFARLAND C D.Near real－teime closed－loop optimal control feedback for spacecraft attitude maneuvers[D].Wright－Pattersn AFB， Ohio： Air Force Institute of Technology，Air University，USAF，2009.

[5]BOLLINO K P，OPPENHEIMER M W.Optimal guidance command generation and tracking for reusable launch vehicle reentry，AFRL－VA－WP－TP－2006－326[R].2006.

[6]LU Ping，DOMAN D B，SCHIERMAN J D.Adaptive terminal guidance for hypervelocity impact in specified diretion[R].Charlottesville，VA：Barron Associates，Inc.，2006.

[7]ASHWINI R，DEBASISH G.State－dependent riccati－equation－based guidance law for impact－angle－constrained trajectories[J].Journal of Guidance，Control and Dynamics，2009，32（1）：320－325.

[8]OZA H B，PADHI R P.A nonlinear suboptimal guidance law with 3Dimpact angle constraints for ground targets，AIAA 2010－8185[R].2010.

[9]LAM V C.Circular guidance laws with and without terminal velocity direction constraints，AIAA 2008－7 304[R].2008.

[10]LU Ping，DOMAN D B，SCHIERMAN J D.Adaptive terminal guidance for hypervelocity impact in specified direction，OMB No.0704－0138[R].2006.

[11]陈海东，余梦伦，董利强.具有终端角度约束的机动再入飞行器的最优制导律[J].航天控制，2002，20（1）：7－10.CHEN Hai－dong，YU Meng－lun，DONG Li－qiang.An optimal guidance law of maneuvering reentry vehicles with terminal angular constraint[J].Aerospace Control，2002，20（1）：7－10.（in Chinese）

[12]刘运鹏，李伶.高超声速导弹高空再入减速段弹道优化设计[J].航天控制，2010，28（6）：4－6.LIU Yun－peng，LI Ling.The optimization design for high－altitude reentry deceleration trajectory of hypersonic missile[J].Aerospace Control，2010，28（6）：4－6.（in Chinese）

[13]孙未蒙，骆振，郑志强.一种多约束下高超声速导弹对地攻击的三维最优变结构制导律[J].国防科技大学学报，2007，29（3）：126－130.SUN Wei－meng，LUO Zhen，ZHENG Zhi－qiang.Three－dimensional optimal variable structure guidance law with multiple constraints in ground strike of hypersonic air－to－surface missile[J].Journal of National University of Defense Technology，2007，29（3）：126－130.（in Chinese）

[14]康兴无，陈刚.天对地精确攻击武器末端制导律研究[J].固体火箭技术，2009，32（1）：11－14.KANG Xing－wu，CHEN Gang.A terminal law design applied to space－to－surface precision attack weapon[J].Journal of Solid Rocket Technology，2009，32（1）：11－14.（in Chinese）

[15]童春霞，张天桥.倾斜转弯导弹的变结构制导律研究[J].弹箭与制导学报，2005，25（3）：8－11.TONG Chun－xia，ZHANG Tian－qiao.Research on variable structure guidance law based on trending－law for BTT missile[J].Journal of Projectiles Rockets Missiles and Guidance，2005，25（3）：8－11.（in Chinese）

[16]孙未蒙，郑志强.一种多约束条件下的三维变结构制导律[J].宇航学报，2007，28（2）：343－349.SUN Wei－meng，ZHENG Zhi－qiang.A new variable structure guidance law of three dimensional with multiple cons－traints[J].Journal of Astronautics，2007，28（2）：343－349.（in Chinese）

[17]赵汉元.飞行器再入动力学和制导[M].长沙：国防科技大学出版社，1997：214－238.ZHAO Han－yuan.Reentry dynamics and guidance[M].Changsha：National University of Defense Technology Press，1997：214－238.（in Chinese）

[18]马先龙，周军.基于滑模控制的末端能量管理方法[J].飞行力学，2007，25（3）：30－33.MA Xian－long，ZHOU Jun.Sliding mode control of terminal area energy management[J].Flight Dynamics，2007，25（3）：30－33.（in Chinese）

[19]沈宏良，龚正.航天飞机末端能量管理段在线轨迹设计方法[J].宇航学报，2008，29（2）：430－433.SHEN Hong－liang，GONG Zheng.Methodology of onboard trajectory design for space shuttle terminal area energy management phase[J].Journal of Astronautics，2008，29（2）：430－433.（in Chinese）