基于运动估计结合小波分析和运动补偿的视频去噪方法



基于运动估计结合小波分析和运动补偿的视频去噪方法

冯长江，毛博，薛冰

（军械工程学院，河北石家庄050003）

摘要：在小波变换理论基础上，提出对视频的运动估计量进行处理来达到视频去噪的方法。首先使用运动域细化技术和全新的基于运动补偿的时间域滤波器，解决含有虚假运动矢量的实时视频去噪问题，提高对动态目标追踪的准确性，增强鲁棒性；并且改进空间域滤波器，降低处理的复杂度。实验结果表明：该方法是一种较为简单且高效的视频去噪方法。

关键词：图像增强；运动估计；视频编码；小波变换

收到修改稿日期：2012-06-11

0　引　言

快速准确地对运动目标识别和跟踪一直是图像处理领域研究的热点。然而视频序列中的噪声，提高了图像的熵，从而降低视频压缩性能，影响目标识别的准确性。目前对集成视频编码的去噪问题并没有理想的处理方式，最为常用的去噪方式大多基于小波变换[1]，这是因为该方法能够在确保视频的质量、分辨率和时间域的可扩展性的同时保证视频的压缩性能。然而大量实验证明，小波变换去噪方法主要基于像素的运动检测技术，因此不能很好地去除视频中的虚假运动元素和虚假运动矢量，从而造成识别的错误[2]。为解决这一问题，本文在小波变换理论基础上，提出了一种基于运动估计的视频去噪方法。其实质是将运动估计中每帧中相对位置改变较小的运动矢量看作标量，与原有滤波器共同作为下一帧的去噪依据，以达到除去虚假运动分量的目的，进而可以准确识别动态目标。

1　算法实现

本文提出的方案如图1所示，空间域滤波器前面并没有使用传统的小波去噪，而是一种新的时间域滤波方式，它包含运动域滤波器和运动补偿滤波器，前者主要用于更精确地检测视频序列中的运动矢量，后者则是修正运动矢量的位置。通过时间域滤波处理后的剩余噪声在空间域上是非平稳的，这就需要根据噪声方差利用小波分析技术进行平滑处理。通过两次滤波后可以准确地找到视频中的运动矢量并排除虚假的运动矢量，从而达到精确识别运动目标的目的。

1.1运动域滤波器

运动估计就是寻找最优或次优的运动向量的过程。本文提出一种基于运动估计而改进的运动域滤波器，它能够有效地从视频帧中找到虚假运动元素的存在并将其消除，从而有效地抑制虚假的背景运动矢量对识别带来的影响。传统方法是比较空间域和时间域中的运动矢量的绝对差均值（包括零运动分量）来判断运动矢量的存在性。然而处理过程中发现背景中的虚假运动估计矢量依然存在，这是因为该方法在计算中降低了图像中运动矢量的绝对差均值（MAD），并且缩小了搜索区域[3]，因而在此基础上进行了优化。本文提出的方法是通过比较相应区域的绝对差均值和总体的绝对差均值来判断运动的存在与否。首先，通过比较当前相应的块中的像素和前一帧的像素，计算出绝对差均值Dk

γ取不同值时，发现当0.4＜γ＜0.5时视频序列产生最好的实验效果（如图2所示），这是因为当γ过大时将会忽略一些运动分量的存在；相反，γ过小时会将背景的微小移动作为运动分量。图2中还发现在0.4＜γ＜0.5以外的区域，均方误差随γ变化的幅度较小。

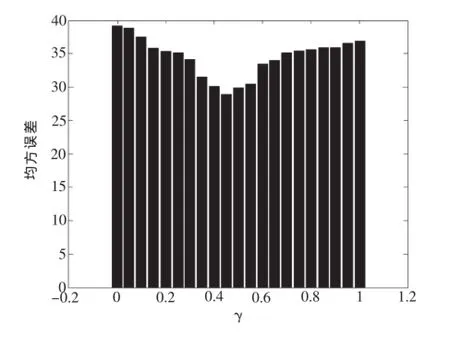
图2　实验效果直方图

在滤波的过程中，要通过比较运动检测阈值THR与每帧中块的运动分量的绝对差均值来确定每个块中是否有运动存在。若，则认为该块中无运动矢量，那么将所有运动矢量分量置0，否则保留它的原始值。

1.2时间域运动补偿滤波器

通过运动域滤波器后的视频信号，由于基于运动轨迹估计的去噪方法能够准确地估计运动分量是否存在，因而大部分虚假运动分量被“过滤”。然而使用该这种方法常常得到错误的运动矢量坐标[4]。为了解决这一问题，应更多地考虑运动估计的可行性，并采用合适的平滑处理。本文提出了一种基于运动补偿的时间域递归滤波去噪方法，能够较好地解决这一问题。

这种滤波器的主要原理是运用运动检测变量mk

mki，j控制时间域平滑量的强弱。对于没有检测到运动矢量的坐标，则使用标准的时间域递归滤波器；而对于检测到运动矢量的坐标，依然要对其进行滤波。但是要针对运动轨迹的估计，采用不同的滤波系数[5]，使用运动估计的方法来估计上述预测误差的存在性，因此在这里要考虑运动估计不完全正确以及该区域是否移动，采取不同程度的时域平滑处理。其方法如下：

首先定义预测误差εki，j，那么在块（i，j）中第k帧的误差为

然后根据预测误差的定义，改进了运动补偿的滤波方式。运动补偿是一种描述相邻帧差别的方法，具体来说是描述前面一帧的每个小块怎样移动到当前帧中的某个位置去。这种方法经常被视频压缩/视频编解码器用来减少视频序列中的时域冗余，它也可以用来进行去除交织以及运动插值的操作。本方法基于此对视频序列进行平滑处理，运动补偿滤波器的表达式为

1.3空间域滤波器

为降低处理的复杂度，使用基于模糊小波图像收缩的降噪技术[6]Fuzzy Shrink算法），这是一种改进的Prob Shrink小波去噪算法[7-8]。该方法使用根据条件随区域可变的小波系数，可以有效迅速消除数字灰度图像加性高斯噪声。定义小波系数均值的表达式为式中：i，j——像素的坐标；

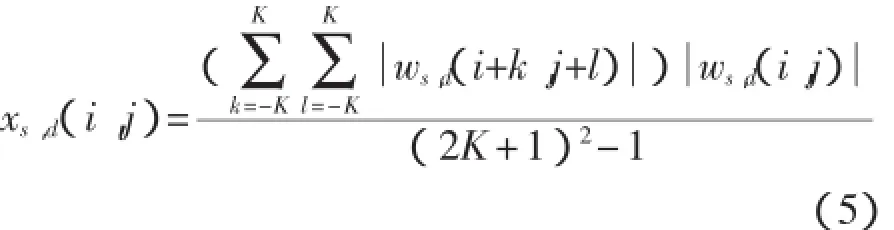
ws，d（i，j）——在坐标（i，j）的小波系数；

2K+1——窗函数的宽度；

xs，d（i，j）——在（2K+1）×（2K+1）区域内小波系数的均值。

Fuzzy Shrink算法是通过比较ws，d（i，j）和xs，d（i，j）来决定小波系数。如果ws，d（i，j）和xs，d（i，j）同时为一个较大的值时，就选择ws，d（i，j）作为去噪的小波系数。

对于均匀方差的噪声，Fuzzy Shrink算法可以得到理想的峰值信噪比（PSNR）。然而通过时间域滤波器处理后的噪声方差是非均匀的，提出对Fuzzy Shrink的修改方法，使之更适应空间非平稳的估计噪声估计量σ。使用分辨率为16×16的重叠窗口，对前面检测出的运动矢量坐标同时沿着不同的方向移动，每次移动8个像素。对于每一个窗口，取Donoho小波域的中位数估计值即最高频率子带中得到的小波系数的0.675作为标准。

2　实验结果及分析

分析本文提出的方法并与WST法进行了对比。使用了3个标准测试序列：“序列1”、“序列2”和“序列3”，并给它们分别加入标准差为σ=10，15，15的白高斯噪声。测试序列的分辨率均为352×240。本文所有实验的运行环境均为酷睿I5，2G内存，显存512M，Windows7，Matlab 2008a。

2.1运动域细化理论

为评估本文所提出的运动域滤波器的效果，对在运动域估计中是否使用运动域细化得到运动补偿帧的均方误差（MSE）进行比较。均方误差是指参数估计值与参数真值之差平方的期望值，是衡量“平均误差”的一种较方便的方法，可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据精确度越高。

运动域均方误差的定义式为

式中：Nx，Ny——运动矢量的组成部分；Nx×Ny——图像大小。

选取一段分辨率为352×240的视频序列进行实验。通过实验观察到，运动域细化后测试序列运动补偿的均方误差明显降低，证明了运动域滤波器的效果十分明显。

通过比较运动过程中是否使用运动域细化得到去噪序列的PSNR均值结果，评估运动域细化的效果。峰值信噪比（PSNR）是一种评价图像的客观标准。在经过影像压缩之后，输出的影像通常都会与原始影像有某种程度不同。为了衡量经过处理后的影像品质，通常会参考PSNR值来认定某个处理程序是否令人满意。定义如下：

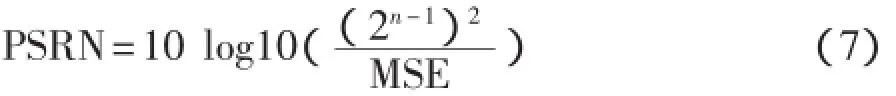
经过运动域细化理论处理后的视频序列的PSNR的均值结果如表1所示，视频的品质得到明显改善。

表1　是否对视频序列使用运动域滤波器去噪得到PSNR的均值

滤波后的运动域出现更好的视觉效果。运动域细化处理前后对比，由于在没有实际运动存在（运动矢量分量为零）的平滑区域，虚假的运动矢量被“过滤”，因而运动域被描绘为战车预期的位置，如图3所示。

图3　视频序列3运动域使用滤波器前后对比

2.2去噪结果

本节中将按照本文方法处理后得到视频的峰值信噪比（PSNR）与在使用基于小波的时间域-空间域滤波的视频序列降噪法（WST）得到的结果进行比较，这里按照测试序列PSNR的平均值作为参考标准。

图4是使用本文提出的方法与WST法进行处理对比结果。经过本文提出的方法进行处理的视频序列在测试序列中表现出更好的结果。使用本文方法去噪后图像的峰值信噪比（PSNR）得到了改善，与WST法比较能够提高1dB。其主要原因是该方法能够较好地去除图像的纹理，同时保持良好的静态图像边缘。由于视频序列1与视频序列2相比纹理相对较少，因此与其他去噪方法相比的差异不是很大，优势不是很明显。

图5是视频序列2的去噪结果。通过对比图4与图5，本文的方法在视频去噪方面胜过其他参考的方法，尤其是在图5序列中包含较多运动元素的情况下，本文的方法体现出更大的优势。此外，在每帧的显示中，低频噪声分量很难被感知，然而使用本方

图4　视频序列1对比实验结果

法处理视频序列能够较好地处理低频噪声分量。特别是在图5中与WST方法相比能够更好地保留图像的纹理，抑制了模糊，静态空间地区的战车边缘清晰可见，其他图像就较为模糊了。

图5　视频序列2对比实验结果

图6是对于视频序列2本文方法与几种常用视频去噪技术的性能比较，其中蓝线表示使用本文方法去噪后视频的PSNR，黑线表示使用WST法后的视频PSNR。使用该方法去噪后视频的PSNR值明显优于其他方法[9-11]。

将该方法与最近提出的视频迭代去噪算法进行比较[12-13]。视频序列1，输入的峰值信噪比为28dB，使用本文方法进行去噪后的峰值信噪比为30.8dB，与迭代法比较高出近0.5dB。对于视频序列2，其峰值信噪比为28dB，使用本文方法后，其峰值信噪比变为34.61dB，使用迭代法为35.13dB。更重要的是，迭代法与本文提出的方法相比要复杂得多。例如使用迭代法，配置为4×3 GHz的处理器去处理分辨率为352×288的视频序列，每帧大约需要4 s；使用本文方法对相同视频序列进行处理，配置为更低速的处理器（双核2.4 GHz），每帧大约需要使用29ms。此外，使用迭代法需要缓存7帧的数据；而本文的方法只需要使用当前帧以及前一帧，这对串行处理的硬件设备来说具有较大意义。

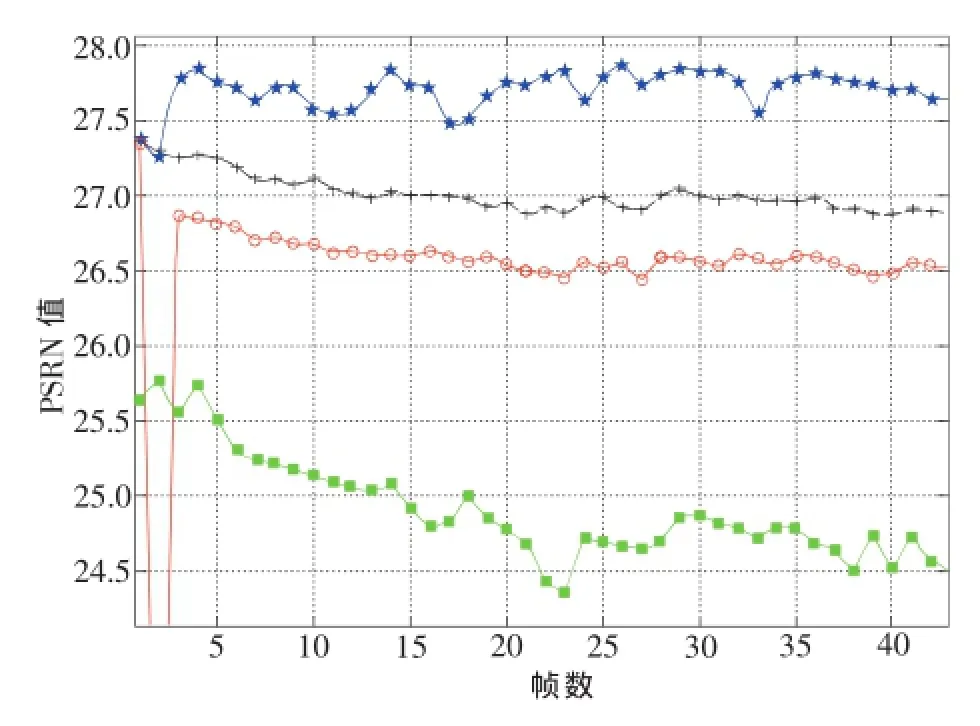
图6　本文方法与WST法性能比较

3　结束语

本文提出对视频序列中的运动估计资源进行再利用，降低了处理的复杂度以及视频解码积分的难度，从而达到降低去噪的难度。本方法的核心由基于运动估计的运动域滤波器以及在这种运动域滤波器基础上提出的时间域递归滤波器两部分组成。实验结果表明，这是一种在降低复杂度的同时高效优异的视频去噪方法。

参考文献

[1] Daubechies I. The wavelet transform，time-frequency localization and signal analysis[J] . IEEE Trans on Information Theory，1990，36（5）：961-1005.

[2] Rahman S M M，Ahmad M O，Swamy M. Video denoising based on inter-frame statistical modeling of wavelet coefficients[J] . IEEE Trans Circuits Syst Video Technol，2007，17（2）：187-199.

[3] Liu B，Zaccarin A. New fast algorithms for the estimation of block motion vectors[J] . IEEE Trans Circuits Syst Video Technol，1993，18（3）：148-157.

[4] Jovanov L，Pizurica A，Schulte S，et al. Combined wavelet-domain and motion-compensated video denoising based on video codec motion estimation methods [J] . IEEE Trans Circuits Syst Video Technol，2009，19（3）：417-421.

[5] Balster E J，Zheng Y F，Ewing R L. Combined spatial and temporal domain wavelet shrinkage algorithm for video denoising[J] . IEEE Trans Circuits Syst for Video Technol，2006，16（2）：220-230.

[6] Saeedi J，Moradi M H，Faez K. A new wavelet-based fuzzy single and multi-channelimage denoising[J] . Image and Vision Computing，2010，28（8）：1611-1623.

[7] Pizurica A，Philips W. Estimating the probability of the presence of a signal of interest in multiresolution single and multiband image denoising[J] . IEEE Transactions on Image Processing，2006，15（3）：654-673.

[8] 王曜，朱光喜，刘玮.结合小波预处理的图像编码方案[J] .计算机应用研究，2003，26（2）：240-243.

[9] 高祖昌，苏岗，黄金，等.小波分析在PWM整流器去噪中的研究[J] .中国测试技术，2008，34（5）：119-121.

[10] 郭兰英.第二代小波基本理论及其在图像压缩中的应用[R] .武汉：武汉大学，2005.

[11] 吴昌东.基于非下采样Contourlet变换的图像去噪方法[J] .西华大学学报：自然科学版，2011，30（6）：19-21.

[12] 王有伟，王渊锋，徐公权.图像定位算法的设计与实现[J] .计算机研究与发展，2002，39（6）：733-736.

[13] 张磊，涂国防.一种新型小波域运动估计算法[J] .电子与信息学报，2007，29（5）：1131-1134.

Video denoising method based on motion estimation combined with wavelet-domain and motion-compensated

FENG Chang-jiang，MAO Bo，XUE Bing

（Ordance Engineering College，Shijiazhuang 050003，China）

Abstract:On the basis of wavelet transform theory，a novel video denoising method is presented in this paper，which reuses motion estimation resources from the video coding module. Firstly，it proposed a novel motion-field filtering step that refines the accuracy of the motion estimates to a degree that is required for denoising. Secondly，a novel temporal filter was proposed that is robust against errors in the estimated motion field. Then spatial domain filter was improved to reduce the complexity of the processing. The experimental results show that the proposed method is a relatively simple and efficient in video denoising.

Key words:image enhancement；motion estimation；video coding；wavelet transform

基金项目：国防科技重点实验室基金项目（9140C8702020803）

收稿日期：2012-04-16；

doi：10.11857/j.issn.1674-5124.2013.05.001

文章编号：1674-5124（2013）05-0001-05

文献标志码：A

中图分类号：TP312；TP391.41；TN949.6+3；TM930.12

作者简介：冯长江（1964-），男，河北石家庄市人，教授，研究方向为电子设计自动化、自动测试系统设计、故障诊断等。